沪科版数学七年级下册 10.2 平行线的判定 教案(表格式)
文档属性
| 名称 | 沪科版数学七年级下册 10.2 平行线的判定 教案(表格式) | 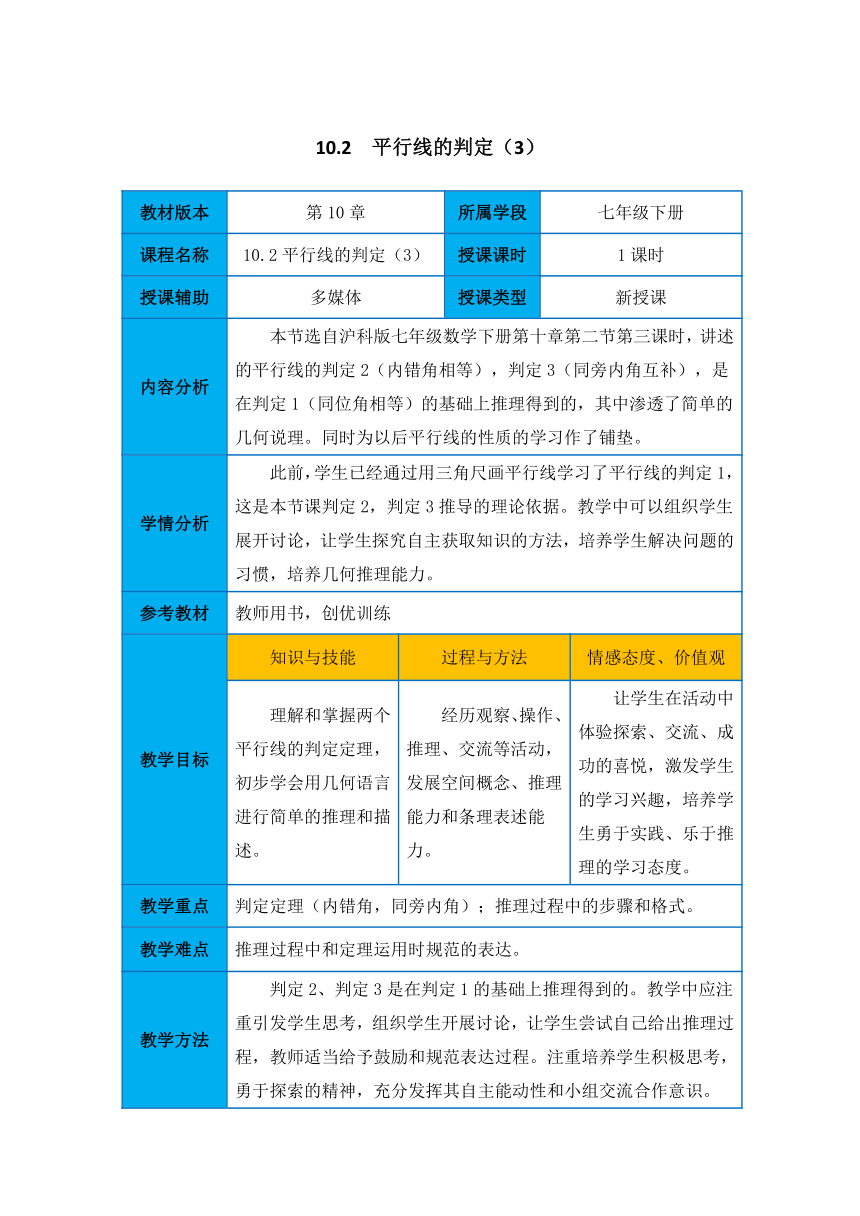 | |
| 格式 | docx | ||
| 文件大小 | 63.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-21 16:52:55 | ||
图片预览


文档简介
10.2 平行线的判定(3)
教材版本 第10章 所属学段 七年级下册
课程名称 10.2平行线的判定(3) 授课课时 1课时
授课辅助 多媒体 授课类型 新授课
内容分析 本节选自沪科版七年级数学下册第十章第二节第三课时,讲述的平行线的判定2(内错角相等),判定3(同旁内角互补),是在判定1(同位角相等)的基础上推理得到的,其中渗透了简单的几何说理。同时为以后平行线的性质的学习作了铺垫。
学情分析 此前,学生已经通过用三角尺画平行线学行线的判定1,这是本节课判定2,判定3推导的理论依据。教学中可以组织学生展开讨论,让学生探究自主获取知识的方法,培养学生解决问题的习惯,培养几何推理能力。
参考教材 教师用书,创优训练
教学目标 知识与技能 过程与方法 情感态度、价值观
理解和掌握两个平行线的判定定理,初步学会用几何语言进行简单的推理和描述。 经历观察、操作、推理、交流等活动,发展空间概念、推理能力和条理表述能力。 让学生在活动中体验探索、交流、成功的喜悦,激发学生的学习兴趣,培养学生勇于实践、乐于推理的学习态度。
教学重点 判定定理(内错角,同旁内角);推理过程中的步骤和格式。
教学难点 推理过程中和定理运用时规范的表达。
教学方法 判定2、判定3是在判定1的基础上推理得到的。教学中应注重引发学生思考,组织学生开展讨论,让学生尝试自己给出推理过程,教师适当给予鼓励和规范表达过程。注重培养学生积极思考,勇于探索的精神,充分发挥其自主能动性和小组交流合作意识。
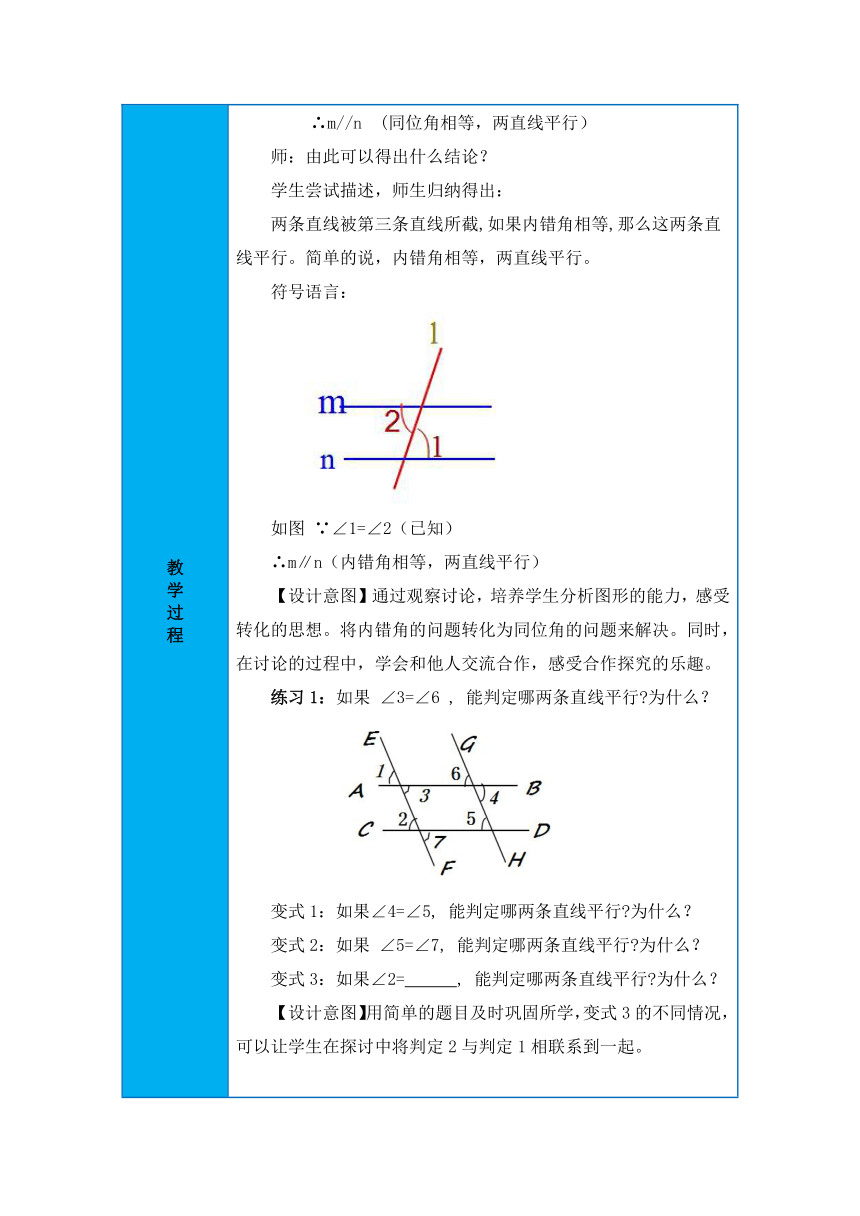
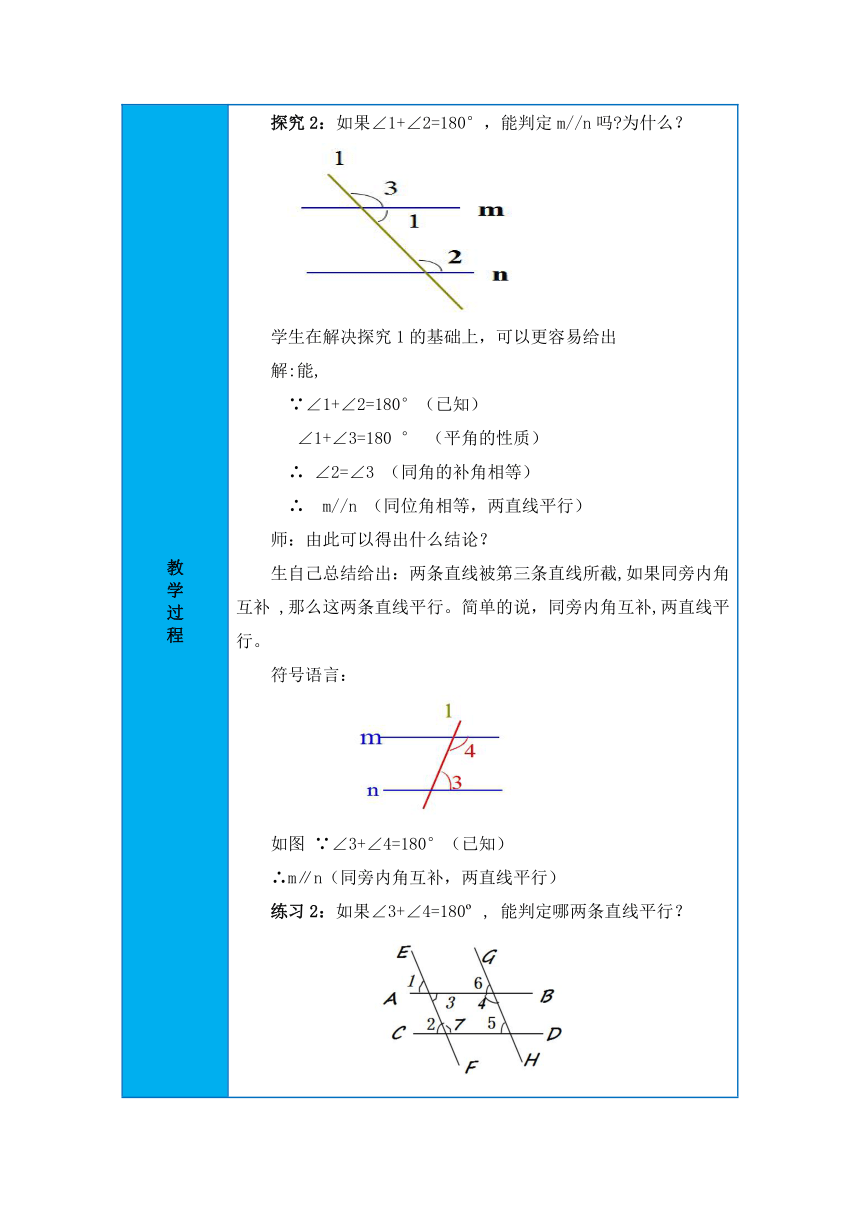
教 学 过 程 教 学 过 程 教 学 过 程 教 学 过 程 教 学 过 程 教 学 过 程 复习导入 师:我们已经学习了哪些判定两条直线平行的方法? 学生讨论交流,归纳给出4种方法: (1)定义:在同一平面内,不相交的两条直线叫平行线。 (2)如果两条直线都和第三条直线平行,那么这两条直线也平行。 (3)在同一平面内,垂直于同一条直线的两条直线平行。 (4)同位角相等,两直线平行. 【设计意图】巩固复习前面所学的判定方法,并由(4)引出今天的学习内容。 二、合作探究 师:两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角。由同位角相等可以判定两直线平行。那么,能否利用内错角,或同旁内角来判定两直线平行呢? 教师提出问题,引发思考,师生共同探究。 探究1:如图,由∠3= ∠2,可推出m//n吗? 如何推出?写出你的推理过程。 生:交流给出 解:∵ ∠1=∠3(对顶角相等) ∠3= ∠2(已知) ∴∠1= ∠2 (等量代换) ∴m//n (同位角相等,两直线平行) 师:由此可以得出什么结论? 学生尝试描述,师生归纳得出: 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。简单的说,内错角相等,两直线平行。 符号语言: 如图 ∵∠1=∠2(已知) ∴m∥n(内错角相等,两直线平行) 【设计意图】通过观察讨论,培养学生分析图形的能力,感受转化的思想。将内错角的问题转化为同位角的问题来解决。同时,在讨论的过程中,学会和他人交流合作,感受合作探究的乐趣。 练习1:如果 ∠3=∠6 , 能判定哪两条直线平行 为什么? 变式1:如果∠4=∠5, 能判定哪两条直线平行 为什么? 变式2:如果 ∠5=∠7, 能判定哪两条直线平行 为什么? 变式3:如果∠2= , 能判定哪两条直线平行 为什么? 【设计意图】用简单的题目及时巩固所学,变式3的不同情况,可以让学生在探讨中将判定2与判定1相联系到一起。 探究2:如果∠1+∠2=180°,能判定m//n吗 为什么? 学生在解决探究1的基础上,可以更容易给出 解:能, ∵∠1+∠2=180°(已知) ∠1+∠3=180 ° (平角的性质) ∴ ∠2=∠3 (同角的补角相等) ∴ m//n (同位角相等,两直线平行) 师:由此可以得出什么结论? 生自己总结给出:两条直线被第三条直线所截,如果同旁内角互补 ,那么这两条直线平行。简单的说,同旁内角互补,两直线平行。 符号语言: 如图 ∵∠3+∠4=180°(已知) ∴m∥n(同旁内角互补,两直线平行) 练习2:如果∠3+∠4=180 , 能判定哪两条直线平行? 变式1:如果∠7+∠ =180 , 能判定哪两条直线平行 为什么? 变式2:如果∠5 , 能判定哪两条直线平行 为什么? 【设计意图】让学生口述,培养学生的表述能力。同时可以适当在图形中多标些角,让学生感受相同的两条直线平行,可以通过不同的方法推出。 三、巩固练习 1、如图,不能判定l ∥l 的是 ( ) (A)∠2=∠3 (B)∠1=∠4 (C)∠1=∠2 (D)∠1=∠3 2.如图,已知∠1=30°,∠2或 ∠3满足条件___________,则a//b。 3、如图,填空: (1)∵∠1=∠2 ∴a∥b( ) (2)∵∠2=∠3 ∴b∥c( ) (3)∵∠1=∠3 ∴a∥c( ) (4)∵∠1+∠4= ∴a∥c( ). 4、看图填空 由∠1=∠2,可以得到 ∥ ,依据是 (2)由∠3=∠4,可以得到 ∥ ,依据是 (3)由∠5=∠DAB,可以得到 ∥ ,依据是 (4)要得到AD∥BC,需∠DAB+ =180°,依据是 (5)要得到AB∥DC,需 + =180°,依据是 【设计意图】通过练习,使学生逐步掌握平行线方法的运用。部分题目一题多解,也培养学生的发散思维。 课堂小结 师:想一想,现在我们有多少种平行线的判定方法? 学生思考给出,教师点拨分类 由线判定线 (1)定义:在同一平面内,不相交的两条直线叫平行线。 (2)如果两条直线都和第三条直线平行,那么这两条直线也平行。 (3)在同一平面内,垂直于同一条直线的两条直线平行。 由角判定线 (4)同位角相等,两直线平行. (5)内错角相等,两直线平行。 (6)同旁内角互补,两直线平行。 【设计意图】通过小结帮助学生对平行线的判定方法形成知识体系,同时培养学生归纳总结的能力。 作业设置 必做作业:书本127页、128页习题。 选做作业: 如图,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a与c平行吗?为什么? 如图,直线AB与CD相交于点O,OA平分∠COE,∠1=∠OBD,试判断OE与BD是否平行,并说明理由。 【设计意图】分层布置作业,能使各个层次的学生都得到相应的发展。同时,选做作业也是下一课时的引入。
板书设计 10.2.3平行线的判定(3) 探究1:内错角相等,两直线平行 探究2:同旁内角互补,两直线平行 3、巩固练习 4、课堂小结 5、作业设置
教学反思 在平行线的判定1的基础上,学生在教师的引导下通过独立思考,小组讨论,合作交流,推理出平行线的判定2、判定3,继而适当练习,巩固所学。在教学过程中,学生感受转换思想,培养逻辑思维能力和条理性表达的能力。同时,在合作交流中体会成功的喜悦,激发学生学习数学的兴趣。
教材版本 第10章 所属学段 七年级下册
课程名称 10.2平行线的判定(3) 授课课时 1课时
授课辅助 多媒体 授课类型 新授课
内容分析 本节选自沪科版七年级数学下册第十章第二节第三课时,讲述的平行线的判定2(内错角相等),判定3(同旁内角互补),是在判定1(同位角相等)的基础上推理得到的,其中渗透了简单的几何说理。同时为以后平行线的性质的学习作了铺垫。
学情分析 此前,学生已经通过用三角尺画平行线学行线的判定1,这是本节课判定2,判定3推导的理论依据。教学中可以组织学生展开讨论,让学生探究自主获取知识的方法,培养学生解决问题的习惯,培养几何推理能力。
参考教材 教师用书,创优训练
教学目标 知识与技能 过程与方法 情感态度、价值观
理解和掌握两个平行线的判定定理,初步学会用几何语言进行简单的推理和描述。 经历观察、操作、推理、交流等活动,发展空间概念、推理能力和条理表述能力。 让学生在活动中体验探索、交流、成功的喜悦,激发学生的学习兴趣,培养学生勇于实践、乐于推理的学习态度。
教学重点 判定定理(内错角,同旁内角);推理过程中的步骤和格式。
教学难点 推理过程中和定理运用时规范的表达。
教学方法 判定2、判定3是在判定1的基础上推理得到的。教学中应注重引发学生思考,组织学生开展讨论,让学生尝试自己给出推理过程,教师适当给予鼓励和规范表达过程。注重培养学生积极思考,勇于探索的精神,充分发挥其自主能动性和小组交流合作意识。
教 学 过 程 教 学 过 程 教 学 过 程 教 学 过 程 教 学 过 程 教 学 过 程 复习导入 师:我们已经学习了哪些判定两条直线平行的方法? 学生讨论交流,归纳给出4种方法: (1)定义:在同一平面内,不相交的两条直线叫平行线。 (2)如果两条直线都和第三条直线平行,那么这两条直线也平行。 (3)在同一平面内,垂直于同一条直线的两条直线平行。 (4)同位角相等,两直线平行. 【设计意图】巩固复习前面所学的判定方法,并由(4)引出今天的学习内容。 二、合作探究 师:两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角。由同位角相等可以判定两直线平行。那么,能否利用内错角,或同旁内角来判定两直线平行呢? 教师提出问题,引发思考,师生共同探究。 探究1:如图,由∠3= ∠2,可推出m//n吗? 如何推出?写出你的推理过程。 生:交流给出 解:∵ ∠1=∠3(对顶角相等) ∠3= ∠2(已知) ∴∠1= ∠2 (等量代换) ∴m//n (同位角相等,两直线平行) 师:由此可以得出什么结论? 学生尝试描述,师生归纳得出: 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。简单的说,内错角相等,两直线平行。 符号语言: 如图 ∵∠1=∠2(已知) ∴m∥n(内错角相等,两直线平行) 【设计意图】通过观察讨论,培养学生分析图形的能力,感受转化的思想。将内错角的问题转化为同位角的问题来解决。同时,在讨论的过程中,学会和他人交流合作,感受合作探究的乐趣。 练习1:如果 ∠3=∠6 , 能判定哪两条直线平行 为什么? 变式1:如果∠4=∠5, 能判定哪两条直线平行 为什么? 变式2:如果 ∠5=∠7, 能判定哪两条直线平行 为什么? 变式3:如果∠2= , 能判定哪两条直线平行 为什么? 【设计意图】用简单的题目及时巩固所学,变式3的不同情况,可以让学生在探讨中将判定2与判定1相联系到一起。 探究2:如果∠1+∠2=180°,能判定m//n吗 为什么? 学生在解决探究1的基础上,可以更容易给出 解:能, ∵∠1+∠2=180°(已知) ∠1+∠3=180 ° (平角的性质) ∴ ∠2=∠3 (同角的补角相等) ∴ m//n (同位角相等,两直线平行) 师:由此可以得出什么结论? 生自己总结给出:两条直线被第三条直线所截,如果同旁内角互补 ,那么这两条直线平行。简单的说,同旁内角互补,两直线平行。 符号语言: 如图 ∵∠3+∠4=180°(已知) ∴m∥n(同旁内角互补,两直线平行) 练习2:如果∠3+∠4=180 , 能判定哪两条直线平行? 变式1:如果∠7+∠ =180 , 能判定哪两条直线平行 为什么? 变式2:如果∠5 , 能判定哪两条直线平行 为什么? 【设计意图】让学生口述,培养学生的表述能力。同时可以适当在图形中多标些角,让学生感受相同的两条直线平行,可以通过不同的方法推出。 三、巩固练习 1、如图,不能判定l ∥l 的是 ( ) (A)∠2=∠3 (B)∠1=∠4 (C)∠1=∠2 (D)∠1=∠3 2.如图,已知∠1=30°,∠2或 ∠3满足条件___________,则a//b。 3、如图,填空: (1)∵∠1=∠2 ∴a∥b( ) (2)∵∠2=∠3 ∴b∥c( ) (3)∵∠1=∠3 ∴a∥c( ) (4)∵∠1+∠4= ∴a∥c( ). 4、看图填空 由∠1=∠2,可以得到 ∥ ,依据是 (2)由∠3=∠4,可以得到 ∥ ,依据是 (3)由∠5=∠DAB,可以得到 ∥ ,依据是 (4)要得到AD∥BC,需∠DAB+ =180°,依据是 (5)要得到AB∥DC,需 + =180°,依据是 【设计意图】通过练习,使学生逐步掌握平行线方法的运用。部分题目一题多解,也培养学生的发散思维。 课堂小结 师:想一想,现在我们有多少种平行线的判定方法? 学生思考给出,教师点拨分类 由线判定线 (1)定义:在同一平面内,不相交的两条直线叫平行线。 (2)如果两条直线都和第三条直线平行,那么这两条直线也平行。 (3)在同一平面内,垂直于同一条直线的两条直线平行。 由角判定线 (4)同位角相等,两直线平行. (5)内错角相等,两直线平行。 (6)同旁内角互补,两直线平行。 【设计意图】通过小结帮助学生对平行线的判定方法形成知识体系,同时培养学生归纳总结的能力。 作业设置 必做作业:书本127页、128页习题。 选做作业: 如图,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a与c平行吗?为什么? 如图,直线AB与CD相交于点O,OA平分∠COE,∠1=∠OBD,试判断OE与BD是否平行,并说明理由。 【设计意图】分层布置作业,能使各个层次的学生都得到相应的发展。同时,选做作业也是下一课时的引入。
板书设计 10.2.3平行线的判定(3) 探究1:内错角相等,两直线平行 探究2:同旁内角互补,两直线平行 3、巩固练习 4、课堂小结 5、作业设置
教学反思 在平行线的判定1的基础上,学生在教师的引导下通过独立思考,小组讨论,合作交流,推理出平行线的判定2、判定3,继而适当练习,巩固所学。在教学过程中,学生感受转换思想,培养逻辑思维能力和条理性表达的能力。同时,在合作交流中体会成功的喜悦,激发学生学习数学的兴趣。
