华师大版八下数学 17.3.2一次函数的图像 教案
文档属性
| 名称 | 华师大版八下数学 17.3.2一次函数的图像 教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 132.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-22 11:06:53 | ||
图片预览


文档简介
17.3.2一次函数的图像
一、教学目标:
1.理解一次函数和正比例函数的图象是一条直线;
2.能熟练地作出一次函数和正比例函数的图象,会求一次函数与坐标轴的交点坐标;
3.会作出实际问题中的一次函数的图象.
2、教学重点、难点:
重点:画一次函数与正比例函数的图象,能利用一次函数的图象解决实际问题.
难点:利用一次函数的图象解决实际问题.
三、教学方法:
学生自主学习、小组讨论、教师讲授
四、教学过程
教学过程和内容 教师活动 学生活动 二次备课备注
活动1创设情景感悟新知 前面我们学习了用描点法画函数图象的方法,下面请同学们根据画图象的步骤:列表、描点、连线,在同一平面直角坐标系中画出下列函数的图象.y=x;(2)y=x+2;(3)y=3x;(4)y=3x+2. 同学们观察并互相讨论,回答:你所画出的图象是什么形状.
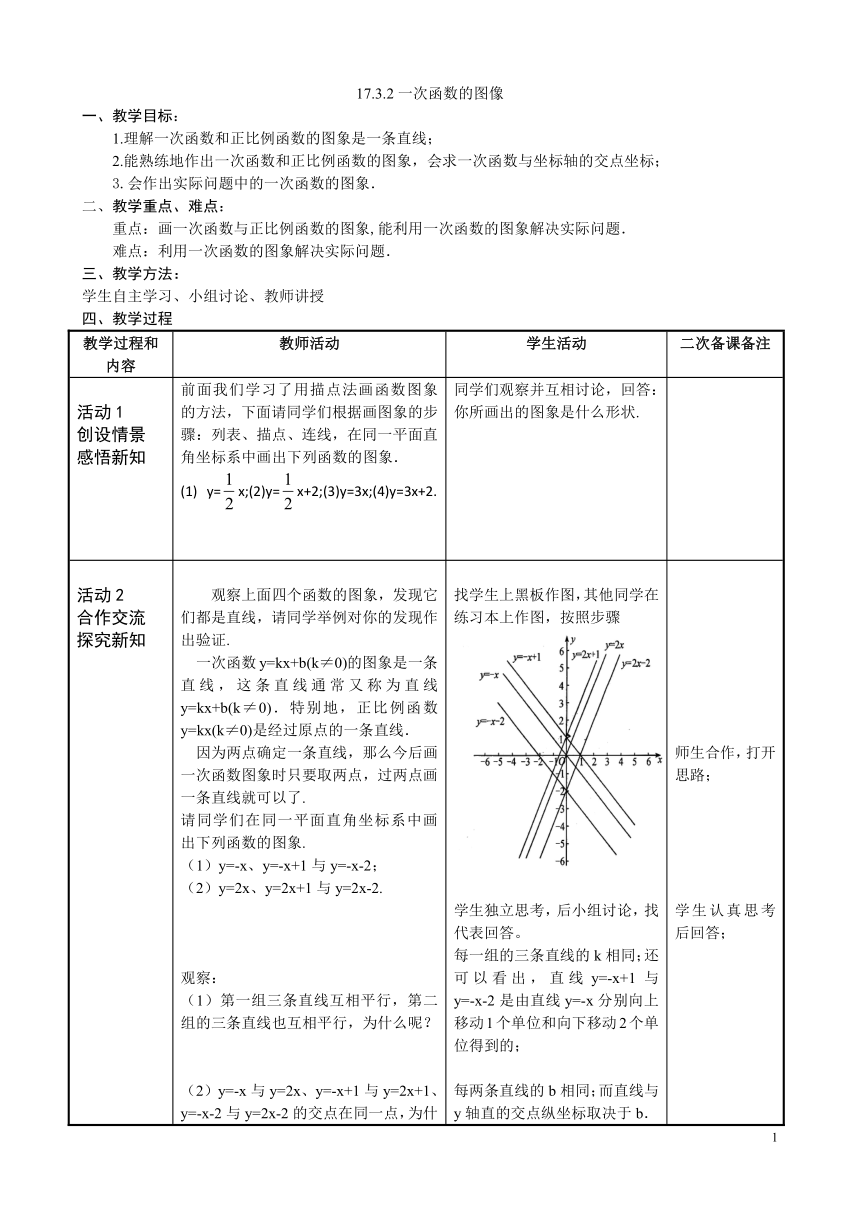
活动2 合作交流探究新知 观察上面四个函数的图象,发现它们都是直线,请同学举例对你的发现作出验证. 一次函数y=kx+b(k≠0)的图象是一条直线,这条直线通常又称为直线y=kx+b(k≠0).特别地,正比例函数y=kx(k≠0)是经过原点的一条直线. 因为两点确定一条直线,那么今后画一次函数图象时只要取两点,过两点画一条直线就可以了.请同学们在同一平面直角坐标系中画出下列函数的图象.(1)y=-x、y=-x+1与y=-x-2;(2)y=2x、y=2x+1与y=2x-2.观察:(1)第一组三条直线互相平行,第二组的三条直线也互相平行,为什么呢?(2)y=-x与y=2x、y=-x+1与y=2x+1、y=-x-2与y=2x-2的交点在同一点,为什么呢? 小结:两个一次函数,当k一样,b不一样时,直线平行。当两个一次函数b一样,k不一样时,它们与y轴交于同一点(0,b); 三、实践应用【例1】在同一平面直角坐标系中画出下列每组函数的图象.(1)y=2x与y=2x+3;(2)y=3x+1与y=x+1.注画出图象后,同学间互相讨论、交流,看看是否与上面的结果一样. 想一想(1)上面每组中的两条直线有什么关系 (2)你取的是哪几个点,互相交流,看谁取的点比较简便. 通过比较,老师点拨,得出结论:一般情况下,取直线与x轴、y轴的交点比较简便.【例2】直线y=-x+3,y=-x-5分别是由直线y=-x经过怎样的移动得到的? 【例3】求直线y=-2x-3与x轴和y轴的交点,并画出这条直线. 【例4】画出问题1中小明距北京的路程s与开车时间t之间函数s=570-95t的图象.分析:在实际问题中,我们可以在表示时间的t轴和表示路程的s轴上分别选取适当的单位长度,画出平面直角坐标系,如图所示.对照画出的函数的图象,请作如下的讨论.讨论:(1)这个函数是不是一次函数 (2)这个函数中自变量t的取值范围是什么 函数的图象是什么 (3)在实际问题中,一次函数的图象除了直线和本题的图形外,还有没有其他情形 找学生上黑板作图,其他同学在练习本上作图,按照步骤学生独立思考,后小组讨论,找代表回答。每一组的三条直线的k相同;还可以看出,直线y=-x+1与y=-x-2是由直线y=-x分别向上移动1个单位和向下移动2个单位得到的;每两条直线的b相同;而直线与y轴直的交点纵坐标取决于b.分析:只要k相同,直线就平行,一次函数y=kx+b(k≠0)的图象是由正比例函数y=kx(k≠0)的图象经过向上或向下平移b个单位得到的.b>o,直线向上移;b<0,直线向下移.y=-x+3是由直线y=-x向上平移3个单位得到的;而y=-x-5是由直线y=-x向下平移5个单位得到的.直线y=-2x-3与x轴的交点问题可以转化为解方程解得所以直线与x轴的交点为(-1.5,0);同样求得直线与y轴的交点为(0,-3). 过点(-1.5,0)和(0,-3)作直线,就是直线y=-2x-3的图象 师生合作,打开思路;学生认真思考后回答;培养学生的观察总结能力
活动3应用迁移练习巩固 1.在同一个平面直角坐标系中画出下列函数的图象,并说出它们有什么关系?(1)y=-2x;(2)y=-2x-4.2.(1)将直线y=3x向下平移2个单位,得到直线;(2)将直线y=-x-5向上平移5个单位,得到直线;(3)将直线y=-2x+3向下平移5个单位,得到直线.3.函数y=kx-4的图象平行于直线y=-2x,求函数的表达式.4.一次函数y=kx+b的图象与y轴交于点(0,-2),且与直线y=3x-12平行,求它们的函数表达式. 学生独立完成并在组内交流疑难问题集中讲评 灵活应用所学知识才能解的题目,需要学生认真思考.
活动4课堂小结 这节课你学到了什么?有何收获?有何困惑?与同伴交流,在学生交流发言的基础上,教师归纳总结. 1.一次函数的图象是一条直线.2.画一次函数图象时,只要取两个点即可,一般取直线与x轴、y轴的交点比较简便.3.两个一次函数,当k一样,b不一样时,共同之处是直线平行,都是由直线y=kx(k≠0)向上或向下平行移动得到,不同之处是它们与y轴的交点不同;当b一样,k不一样时,共同之处是它们与y轴交于同一点(0,b),不同之处是直线不平行. 回顾本节课的知识点,形成系统体系。
活动5作业布置 学习检测、课后练习 独立完成 巩固新知
活动7板书设计 17.3.2一次函数的图像一次函数的图象一次函数的图象是一条直线.平行规律:例1例2例3与x轴交点令y=0,与y轴交点令x=0.例4
活动8教后反思
一、教学目标:
1.理解一次函数和正比例函数的图象是一条直线;
2.能熟练地作出一次函数和正比例函数的图象,会求一次函数与坐标轴的交点坐标;
3.会作出实际问题中的一次函数的图象.
2、教学重点、难点:
重点:画一次函数与正比例函数的图象,能利用一次函数的图象解决实际问题.
难点:利用一次函数的图象解决实际问题.
三、教学方法:
学生自主学习、小组讨论、教师讲授
四、教学过程
教学过程和内容 教师活动 学生活动 二次备课备注
活动1创设情景感悟新知 前面我们学习了用描点法画函数图象的方法,下面请同学们根据画图象的步骤:列表、描点、连线,在同一平面直角坐标系中画出下列函数的图象.y=x;(2)y=x+2;(3)y=3x;(4)y=3x+2. 同学们观察并互相讨论,回答:你所画出的图象是什么形状.
活动2 合作交流探究新知 观察上面四个函数的图象,发现它们都是直线,请同学举例对你的发现作出验证. 一次函数y=kx+b(k≠0)的图象是一条直线,这条直线通常又称为直线y=kx+b(k≠0).特别地,正比例函数y=kx(k≠0)是经过原点的一条直线. 因为两点确定一条直线,那么今后画一次函数图象时只要取两点,过两点画一条直线就可以了.请同学们在同一平面直角坐标系中画出下列函数的图象.(1)y=-x、y=-x+1与y=-x-2;(2)y=2x、y=2x+1与y=2x-2.观察:(1)第一组三条直线互相平行,第二组的三条直线也互相平行,为什么呢?(2)y=-x与y=2x、y=-x+1与y=2x+1、y=-x-2与y=2x-2的交点在同一点,为什么呢? 小结:两个一次函数,当k一样,b不一样时,直线平行。当两个一次函数b一样,k不一样时,它们与y轴交于同一点(0,b); 三、实践应用【例1】在同一平面直角坐标系中画出下列每组函数的图象.(1)y=2x与y=2x+3;(2)y=3x+1与y=x+1.注画出图象后,同学间互相讨论、交流,看看是否与上面的结果一样. 想一想(1)上面每组中的两条直线有什么关系 (2)你取的是哪几个点,互相交流,看谁取的点比较简便. 通过比较,老师点拨,得出结论:一般情况下,取直线与x轴、y轴的交点比较简便.【例2】直线y=-x+3,y=-x-5分别是由直线y=-x经过怎样的移动得到的? 【例3】求直线y=-2x-3与x轴和y轴的交点,并画出这条直线. 【例4】画出问题1中小明距北京的路程s与开车时间t之间函数s=570-95t的图象.分析:在实际问题中,我们可以在表示时间的t轴和表示路程的s轴上分别选取适当的单位长度,画出平面直角坐标系,如图所示.对照画出的函数的图象,请作如下的讨论.讨论:(1)这个函数是不是一次函数 (2)这个函数中自变量t的取值范围是什么 函数的图象是什么 (3)在实际问题中,一次函数的图象除了直线和本题的图形外,还有没有其他情形 找学生上黑板作图,其他同学在练习本上作图,按照步骤学生独立思考,后小组讨论,找代表回答。每一组的三条直线的k相同;还可以看出,直线y=-x+1与y=-x-2是由直线y=-x分别向上移动1个单位和向下移动2个单位得到的;每两条直线的b相同;而直线与y轴直的交点纵坐标取决于b.分析:只要k相同,直线就平行,一次函数y=kx+b(k≠0)的图象是由正比例函数y=kx(k≠0)的图象经过向上或向下平移b个单位得到的.b>o,直线向上移;b<0,直线向下移.y=-x+3是由直线y=-x向上平移3个单位得到的;而y=-x-5是由直线y=-x向下平移5个单位得到的.直线y=-2x-3与x轴的交点问题可以转化为解方程解得所以直线与x轴的交点为(-1.5,0);同样求得直线与y轴的交点为(0,-3). 过点(-1.5,0)和(0,-3)作直线,就是直线y=-2x-3的图象 师生合作,打开思路;学生认真思考后回答;培养学生的观察总结能力
活动3应用迁移练习巩固 1.在同一个平面直角坐标系中画出下列函数的图象,并说出它们有什么关系?(1)y=-2x;(2)y=-2x-4.2.(1)将直线y=3x向下平移2个单位,得到直线;(2)将直线y=-x-5向上平移5个单位,得到直线;(3)将直线y=-2x+3向下平移5个单位,得到直线.3.函数y=kx-4的图象平行于直线y=-2x,求函数的表达式.4.一次函数y=kx+b的图象与y轴交于点(0,-2),且与直线y=3x-12平行,求它们的函数表达式. 学生独立完成并在组内交流疑难问题集中讲评 灵活应用所学知识才能解的题目,需要学生认真思考.
活动4课堂小结 这节课你学到了什么?有何收获?有何困惑?与同伴交流,在学生交流发言的基础上,教师归纳总结. 1.一次函数的图象是一条直线.2.画一次函数图象时,只要取两个点即可,一般取直线与x轴、y轴的交点比较简便.3.两个一次函数,当k一样,b不一样时,共同之处是直线平行,都是由直线y=kx(k≠0)向上或向下平行移动得到,不同之处是它们与y轴的交点不同;当b一样,k不一样时,共同之处是它们与y轴交于同一点(0,b),不同之处是直线不平行. 回顾本节课的知识点,形成系统体系。
活动5作业布置 学习检测、课后练习 独立完成 巩固新知
活动7板书设计 17.3.2一次函数的图像一次函数的图象一次函数的图象是一条直线.平行规律:例1例2例3与x轴交点令y=0,与y轴交点令x=0.例4
活动8教后反思
