指数函数及性质

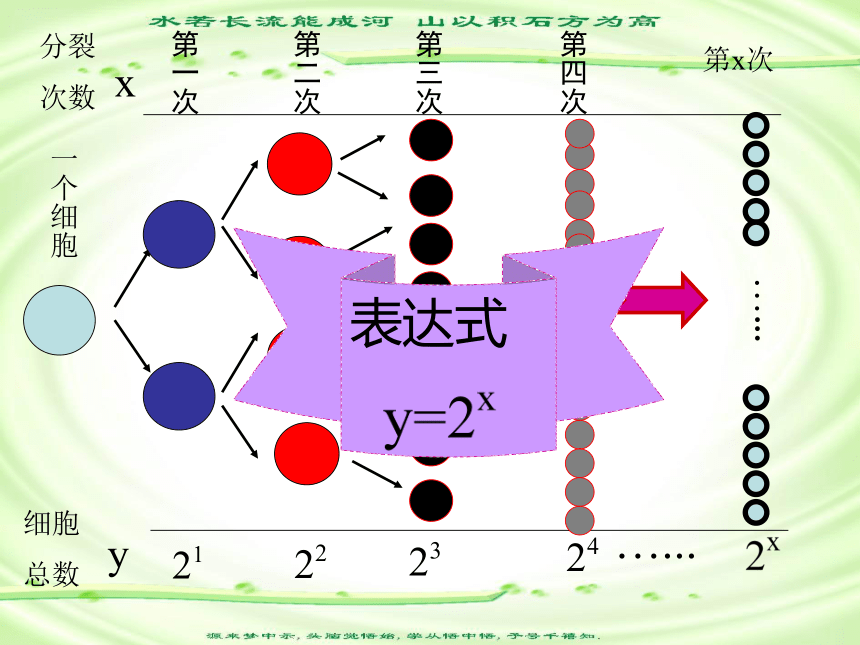
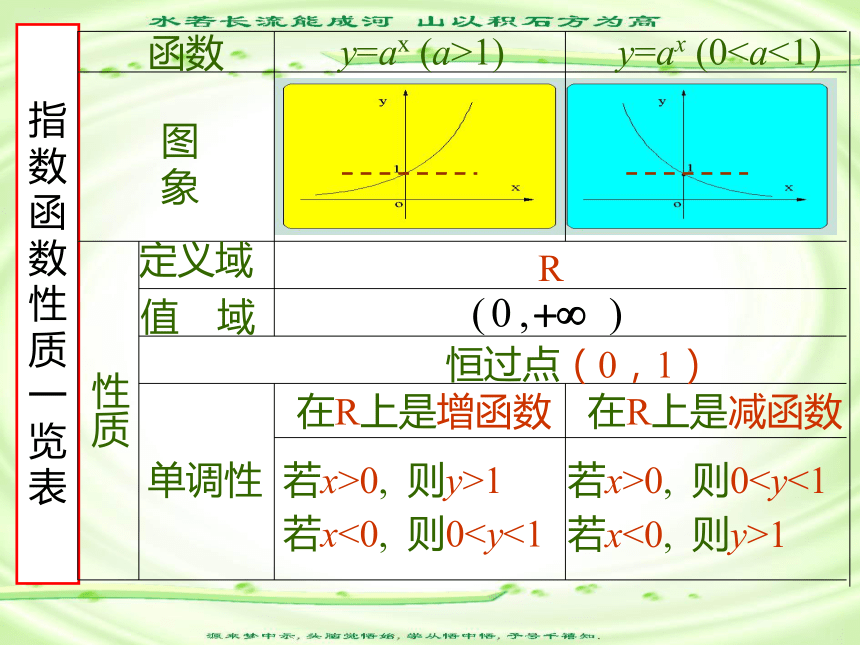
课件42张PPT。2019年1月26日星期六(必修1)第二章 基本初等函数(Ⅰ)2.1指数函数2.1.2 指数函数及其性质某种细胞分裂时,第一次由1个分裂成2个，第2次由2个分裂成4个，如此下去，如果第x次分裂得到y个细胞，那么细胞个数y与分裂次数x的函数关系是什么？引例：1分裂
次数第一次第二次第三次第四次第x次…...x引例：2 一种放射性物质不断衰变为其他物质,每经过一年剩留的质量约是原来的84%.求出这种物质的剩留量随时间(单位:年)变化的函数关系.设最初的质量为1,时间变量用x表示,剩留量用y表示
则 经过1年,经过2年,归纳出:经过x年,思考:这两个例子的式子有什么共同特征?底数是常数,指数是变量注意:(1) 规定无意义是一个常值函数，无研究必要（2）形式的严格性：指数是自变量x，且整个式子的系数是11.指数函数的概念 一般地,形如 (a>0且a≠1)叫做指数函数,
其中x是自变量. 函数的定义域是R. 新疆奎屯市第一高级中学 特级教师王新敞6练习判断下列哪些函数是指数函数.
×××√√√例1.下列函数中指数函数的个数是： 答案：2个范例 -5 -4 -3 -2 -1 0 1 2 3 4 5
9
8
7
6
5
4
3
2
1
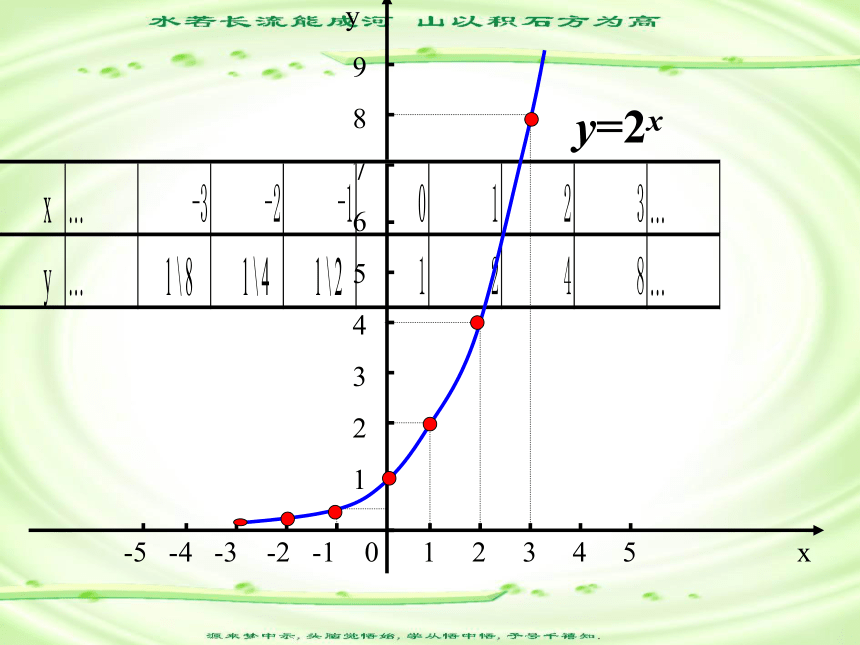
xyy=2x
9
8
7
6
5
4
3
2
1
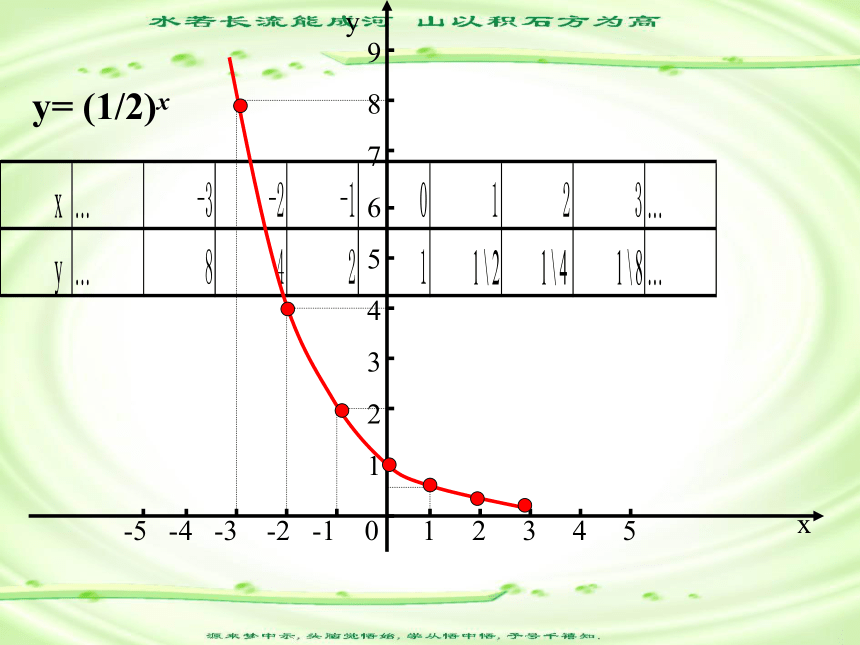
xy -5 -4 -3 -2 -1 0 1 2 3 4 5y= (1/2)x10
9
8
7
6
5
4
3
2
1
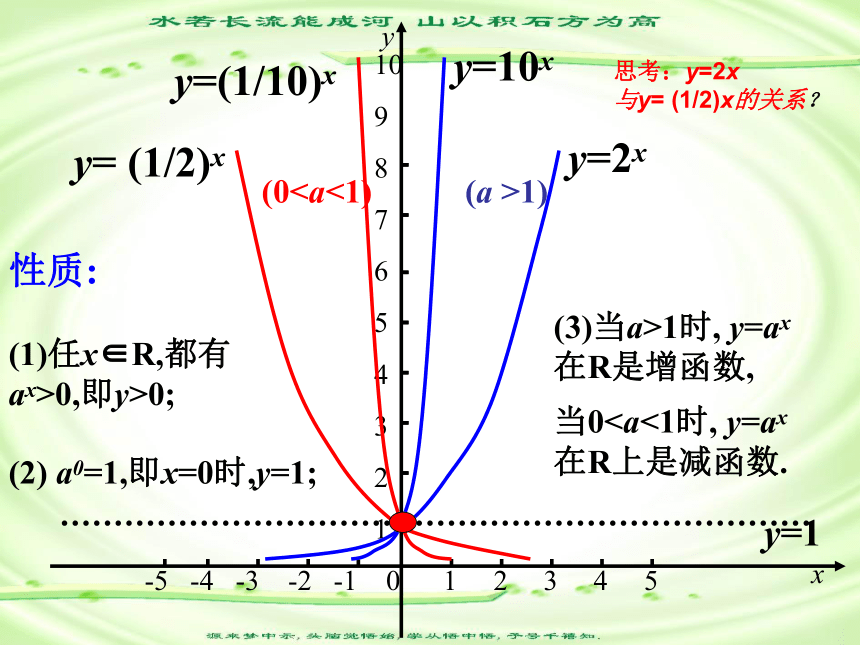
-5 -4 -3 -2 -1 0 1 2 3 4 5xy y=1y=2xy= (1/2)xy=10xy=(1/10)x (a >1) (00,即y>0;(2) a0=1,即x=0时,y=1;(3)当a>1时, y=ax在R是增函数,当0与y= (1/2)x的关系？指数函数性质一览表函数y=ax (a>1)y=ax (0象定义域R值 域性质恒过点（0，1）单调性在R上是增函数在R上是减函数若x>0, 则y>1若x<0, 则01若x>0, 则00且a≠1)的
图像经过点(3， )，求f(0)， f(1)， f(-3)的值。 分析：要求f(0)， f(1)， f(-3)的值，我们需要
先求出指数函数 的解析式，也就是要
先求a的值，根据函数图像过点(3, )这一条件，
可以求得底数a的值。范例解： 因为 的图象经过点(3, ) ,即 解得 ,于是 范例所以例2．已知指数函数 (a>0且a≠1)的
图像经过点(3， )，求f(0)， f(1)， f(-3)的值。解： 范例例3．比较下列各题中两个值的大小:解： 范例例3．比较下列各题中两个值的大小:所以范例例3．比较下列各题中两个值的大小: ⑶因为 不能看作同一个指数函数的两
个函数值，所以我们可以首先在这两个数值中间
找一个数值，将这一个数值与原来两个数值分别
比较大小，然后确定原来两个数值的大小关系。由指数函数的性质知所以范例例3．比较下列各题中两个值的大小:解： y1.如图是指数函数 ① y=ax ② y=bx
③ y=cx ④ y=dx 的图象，则 a,b,c,d 的大小关系（ ） .a b 1 c d
.b a 1 d c
.1 a b c d
.a b 1 d cBABCD①②③④巩固练习badc特级教师 王新敞 源头学子 wxckt@126.com19 【4】指数函数 满足不等式 ,则它们的图象是 (??? ).C.A.B.D.D 2.若函数y=(a-1)x在R上为减函数，则a满足（ ）
0 < a < 1
a > 1
1< a < 2
a > 2 CBADC巩固练习特级教师 王新敞 源头学子 wxckt@126.com21复习回顾1.指数函数:函数y=ax(a>0,且a≠1)叫做指数函数其中x是自变量,函数定义域是R.2.指数函数的图象和性质：特级教师 王新敞 源头学子 wxckt@126.com22 【3】已知函数 f(x)是奇函数,且当x > 0时,f(x)=2x+1,求当x＜0时,f(x)的解析式.又因为f(x)是奇函数,∴ f(-x)=-f(x).解:因为当 x>0 时, ∴当 x ＜0时,-x >0,即所以当x＜0时,特级教师 王新敞 源头学子 wxckt@126.com23图像过定点问题 例2.函数y＝ax-3＋2(a＞0,且a≠1)必经过哪个定点？点评:函数y＝ax-3＋2的图象恒过定点(3,３),实际上就是将定点(0,1)向右平移3个单位,向上平移2个单位得到. 由于函数y＝ax(a＞0,且a≠1)恒经过定点(0,1),因此指数函数与其它函数复合会产生一些丰富多彩的定点问题 特级教师 王新敞 源头学子 wxckt@126.com24 【1】函数y＝ax+5-1（a＞0,且a≠1）必经过哪个定点？变式练习2.图像过定点问题 【2】函数 恒过定点(1,3)则b=____.特级教师 王新敞 源头学子 wxckt@126.com25 例4.设a是实数, (1)试证明对于任意 a, f(x)为增函数；证明:任取x1,x2 ,且f(x1)－f(x2)=∵ y=2x在R上是增函数,且x1＜x2 ,∴f(x1)-f(x2)＜0,即 f(x1)＜f(x2).故 对于a 取任意实数,f(x) 为增函数.4.单调性与奇偶性问题特级教师 王新敞 源头学子 wxckt@126.com26解:若 f ( x ) 为奇函数,则 f(-x )=-f (x),利用 f(0)= 0 例4.设a是实数, (2)试确定a的值,使f(x)为奇函数.∴ a = 1.特级教师 王新敞 源头学子 wxckt@126.com27 【1】已知定义域为R的函数 为奇函数,则a=__, b=_____.变式练习21 【2】设a>0, 在R上为偶函数,(1)求a, (2)证明函数f(x)在(0,+∞)上为增函数.特级教师 王新敞 源头学子 wxckt@126.com28 例1.讨论函数 的单调性,并求其值域.解:任取x1,x2∈(-∞,1],且x1< x2 ,∵f(x1)>0, f(x2)>0,指数形式的复合函数的单调性(奇偶性)则特级教师 王新敞 源头学子 wxckt@126.com29∵ x10, x1+x2-2<0.特级教师 王新敞 源头学子 wxckt@126.com30例2、 （1）已知函数 , 求函数y在[-1，1]上的最大值和最小值.
例3、（2）若 -1≤x≤1 , 恒成立，求a的取值范围特级教师 王新敞 源头学子 wxckt@126.com31【1】函数 的单调增区间是【2】函数 的增区间为 ________. 值域为_________. (－∞,1]练一练【3】求函数 的定义域为________4.求证函数 是奇函数,且是增函数.(0,81]特级教师 王新敞 源头学子 wxckt@126.com32 在同一坐标系下作出下列函数的图象,并指出它们与指数函数y=2x的图象的关系.解：⑴列出函数数据表,作出图像问题1.特级教师 王新敞 源头学子 wxckt@126.com33①将指数函数y=2x的图象向左平行移动1个单位长度,就得到函数y=2x+1的图象;②将指数函数y=2x的图象向右平行移动2个单位长度,就得到函数y=2x-2的图象.归纳总结特级教师 王新敞 源头学子 wxckt@126.com34 【1】若函数f(x) = 3x 2,把图象向右平移 1 个单位,则得到函数 ____________ 的图象；
若把函数 f ( x ) 的图象向左平移2 个单位,则得到函数 ____________ 的图象；
若把函数 f ( x ) 的图象向下平移 3 个单位,则得到函数 _________ 的图象；
若把函数 f ( x ) 的图象向上平移 4 个单位,则得到函数 _________ 的图象.y=3x2+4 y=3(x－1)2y=3(x+2)2y=3x2－3 规律：左加右减；上加下减变式训练特级教师 王新敞 源头学子 wxckt@126.com35 【2】函数y=f(x+1)+1的图象可由函数y=f(x)的图象经过下述哪种变换得到.…………( )
(A)向左平移一个单位，再向上平移一个单位；
(B)向左平移一个单位，再向下平移一个单位；
(C)向右平移一个单位，再向上平移一个单位；
(D)向右平移一个单位，再向下平移一个单位；A(1)y=f(x)?y=f(x+a)上下平移(2)y=f(x)?y=f(x)+k?函数图象的平移变换规律：左右平移特级教师 王新敞 源头学子 wxckt@126.com36 【3】若函数y=ax+b-1(a>0,且a≠1)的图象经过第二、三、四象限,则一定有……( ).特级教师 王新敞 源头学子 wxckt@126.com37例1. 已知函数 作出函数图象,求定义域、
值域,并探讨与图象 的关系.所以,定义域为R,值域为(0,1]. 保留 在y轴右侧的图象,该部分翻折到y轴的左侧,这个关于y轴对称的图形就是
的图象.1两图象关系特级教师 王新敞 源头学子 wxckt@126.com38【3】作出函数 的图像,求定义域、值域. 定义域:R,值域:(0,1].变式训练特级教师 王新敞 源头学子 wxckt@126.com39 说出下列函数的图象与指数函数 y=2x 的图象的关系,并画出它们的示意图.问题2.（x,y)和(-x,y)关于y轴对称！（x,y)和(x,-y)关于x轴对称！（x,y)和(-x,-y)关于原点对称！特级教师 王新敞 源头学子 wxckt@126.com40(1) y=f(x)与y=f(-x)的图象关于 对称； (2) y=f(x)与y=-f(x)的图象关于 对称； (3) y=f(x)与y=-f(-x)的图象关于 对称. x 轴y 轴原 点 特级教师 王新敞 源头学子 wxckt@126.com41 分别在同一坐标系中作出下列各组函数的图象,并说明它们之间有什么关系？ 由 y=f(x) 的图象作 y=f(|x|) 的图象：保留y=f(x)中y轴右侧部分,再加上这部分关于y轴对称的图形.问题3.再见！谢谢！点滴积累 丰富人生