2021-2022学年高一下学期数学人教A版(2019)必修第二册9.1.1简单随机抽样(第2课时)课件(共15张PPT)
文档属性
| 名称 | 2021-2022学年高一下学期数学人教A版(2019)必修第二册9.1.1简单随机抽样(第2课时)课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-22 10:57:57 | ||
图片预览






文档简介
(共15张PPT)
9.1.1 简单随机抽样
(第2课时)
人教2019版必修第二册
第九章 统 计
复习巩固
一般地,总体中有N个个体,它们的变量值分别为Y1,Y2,…,YN,则称
为总体平均值,又称总体平均数.
1.总体平均数
新课讲解
如果总体的N个变量值中,不同的值共有k(k≤N)个,不妨记为Y1,Y2,…,Yk,其中Yi出现的频数fi(i=1,2,…,k),则总体均值还可以写成加权平均数的形式
2.加权平均数
新课讲解
如果从总体中抽取一个容量为n的样本,它们的变量值分别为y1,y2,…,yn,
则称 为样本平均值,又称样本平均数.
3.样本平均值
抽样序号
1 2 3 4 5 6 7 8 9 10
样本量为50:的平均数 165.2 162.8 164.4 164.4 165.6 164.8 165. 3 164.7 165.7 165.0
样本量为100的平均数 164.4 165.0 164.7 164.9 164.6 164.9 165. 1 165.2 165. 1 165.2
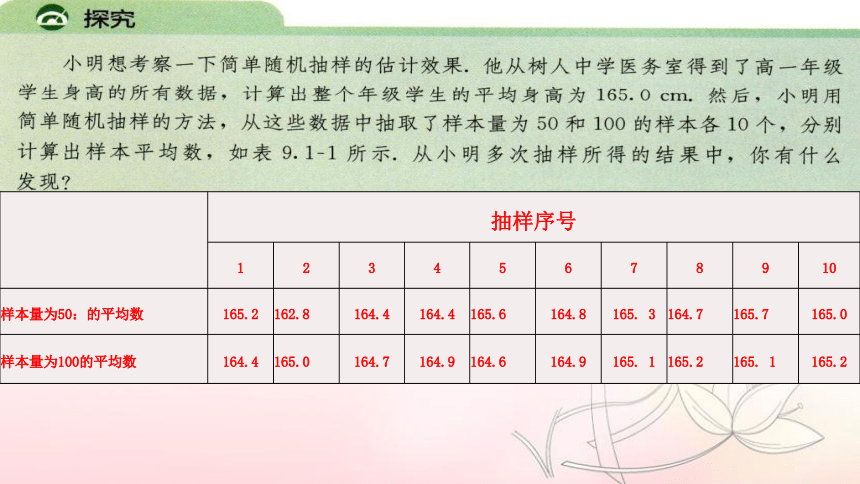
为了更方便地观察数据,以便我们分析样本平均数的特点以及与总体平均数的关系,我们把这20次试验的平均数用图形表示出来,如下图所示。图中的红线表示树人中学高一年级全体学生身高的平均数。
从试验结果看,不管样本量为50,还是为100,不同样本的平均数往往是不同的。由于样本的选取是随机的,因此样本平均数也具有随机性,这与总体平均数是一个确定的数不同。虽然在所有20个样本平均数中,与总体平均数完全一致的很少,但除了样本量为50的第2个样本外,样本平均数偏离总体平均数都不超过1CM,即大部分样本平均数离总体平均数不远,在总体平均数附近波动。 比较样本量为50和样本量为100的样本平均数,还可以发现样本量为100的波动幅度明显小于样本量为50的,这与我们对增加样本量可以提高估计效果的认识是一致的。
问题二:眼睛是心灵的窗户,保护好视力非常重要。树人中学在“全国爱眼日”前,想通过简单随机抽样的方法,了解一下全校2174名学生中视力不低于5.0的学生所占的比例,你觉得该怎样做?总体、个体、变量分别是什么?
我们记“视力不低于5.0”为1,“视力低于5.0”为0,则第i个(i=1,2,...,2174)学生的视力变量值为
例题讲解
问题二:眼睛是心灵的窗户,保护好视力非常重要。树人中学在“全国爱眼日”前,想通过简单随机抽样的方法,了解一下全校2174名学生中视力不低于5.0的学生所占的比例,你觉得该怎样做?总体、个体、变量分别是什么?
例题讲解
现在,我们从树人中学所有学生中抽取一个容量为50的简单随机样本,其视力变量取值如下:
1 1 0 1 0 0 1 0 1 1 1 0 0 0 1 1 0 1 0 0 0 1 1 10 1 1 0 1 1 1 1 0 1 1 0 1 0 1 0 0 0 1 0 0 1 1 1 0 0
由样本平均数,我们估计在树人中学全体学生中,“视力不低于5.0”的比例约为0.54.
问题二:眼睛是心灵的窗户,保护好视力非常重要。树人中学在“全国爱眼日”前,想通过简单随机抽样的方法,了解一下全校2174名学生中视力不低于5.0的学生所占的比例,你觉得该怎样做?总体、个体、变量分别是什么?
例题讲解
随堂练习
1.关于简单随机抽样,下列说法正确的是( )
①它要求被抽取样本的总体的个数有限;②它是从总体中逐个地进行抽取;③不做特殊说明时它是一种不放回抽样;④它是一种等可能性抽样
A.①②③④ B.③④ C.①②③ D.①③④
【解析】根据简单随机抽样的定义和性质知:
①它要求被抽取样本的总体的个数有限,正确;
②它是从总体中逐个地进行抽取,正确;
③不作特殊说明时它是一种不放回抽样,正确;
④它是一种等可能性抽样,正确;故选:
A
A
D
AC
AC
9.1.1 简单随机抽样
(第2课时)
人教2019版必修第二册
第九章 统 计
复习巩固
一般地,总体中有N个个体,它们的变量值分别为Y1,Y2,…,YN,则称
为总体平均值,又称总体平均数.
1.总体平均数
新课讲解
如果总体的N个变量值中,不同的值共有k(k≤N)个,不妨记为Y1,Y2,…,Yk,其中Yi出现的频数fi(i=1,2,…,k),则总体均值还可以写成加权平均数的形式
2.加权平均数
新课讲解
如果从总体中抽取一个容量为n的样本,它们的变量值分别为y1,y2,…,yn,
则称 为样本平均值,又称样本平均数.
3.样本平均值
抽样序号
1 2 3 4 5 6 7 8 9 10
样本量为50:的平均数 165.2 162.8 164.4 164.4 165.6 164.8 165. 3 164.7 165.7 165.0
样本量为100的平均数 164.4 165.0 164.7 164.9 164.6 164.9 165. 1 165.2 165. 1 165.2
为了更方便地观察数据,以便我们分析样本平均数的特点以及与总体平均数的关系,我们把这20次试验的平均数用图形表示出来,如下图所示。图中的红线表示树人中学高一年级全体学生身高的平均数。
从试验结果看,不管样本量为50,还是为100,不同样本的平均数往往是不同的。由于样本的选取是随机的,因此样本平均数也具有随机性,这与总体平均数是一个确定的数不同。虽然在所有20个样本平均数中,与总体平均数完全一致的很少,但除了样本量为50的第2个样本外,样本平均数偏离总体平均数都不超过1CM,即大部分样本平均数离总体平均数不远,在总体平均数附近波动。 比较样本量为50和样本量为100的样本平均数,还可以发现样本量为100的波动幅度明显小于样本量为50的,这与我们对增加样本量可以提高估计效果的认识是一致的。
问题二:眼睛是心灵的窗户,保护好视力非常重要。树人中学在“全国爱眼日”前,想通过简单随机抽样的方法,了解一下全校2174名学生中视力不低于5.0的学生所占的比例,你觉得该怎样做?总体、个体、变量分别是什么?
我们记“视力不低于5.0”为1,“视力低于5.0”为0,则第i个(i=1,2,...,2174)学生的视力变量值为
例题讲解
问题二:眼睛是心灵的窗户,保护好视力非常重要。树人中学在“全国爱眼日”前,想通过简单随机抽样的方法,了解一下全校2174名学生中视力不低于5.0的学生所占的比例,你觉得该怎样做?总体、个体、变量分别是什么?
例题讲解
现在,我们从树人中学所有学生中抽取一个容量为50的简单随机样本,其视力变量取值如下:
1 1 0 1 0 0 1 0 1 1 1 0 0 0 1 1 0 1 0 0 0 1 1 10 1 1 0 1 1 1 1 0 1 1 0 1 0 1 0 0 0 1 0 0 1 1 1 0 0
由样本平均数,我们估计在树人中学全体学生中,“视力不低于5.0”的比例约为0.54.
问题二:眼睛是心灵的窗户,保护好视力非常重要。树人中学在“全国爱眼日”前,想通过简单随机抽样的方法,了解一下全校2174名学生中视力不低于5.0的学生所占的比例,你觉得该怎样做?总体、个体、变量分别是什么?
例题讲解
随堂练习
1.关于简单随机抽样,下列说法正确的是( )
①它要求被抽取样本的总体的个数有限;②它是从总体中逐个地进行抽取;③不做特殊说明时它是一种不放回抽样;④它是一种等可能性抽样
A.①②③④ B.③④ C.①②③ D.①③④
【解析】根据简单随机抽样的定义和性质知:
①它要求被抽取样本的总体的个数有限,正确;
②它是从总体中逐个地进行抽取,正确;
③不作特殊说明时它是一种不放回抽样,正确;
④它是一种等可能性抽样,正确;故选:
A
A
D
AC
AC
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
