数学高中必修四苏教版1.2《任意角的三角函数》课件
文档属性
| 名称 | 数学高中必修四苏教版1.2《任意角的三角函数》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 243.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-04 20:46:41 | ||
图片预览







文档简介
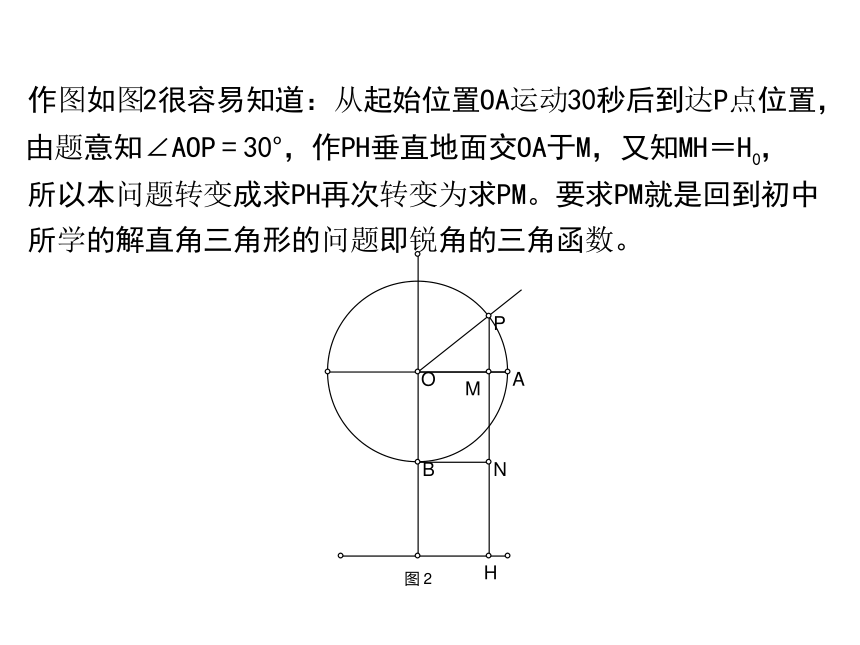
课件61张PPT。1.2.1 任意角的三角函数(1) 问题1:如图是一个摩天轮,假设它的中心离地面的高度为h0,它的直径为2R,逆时针方向匀速转动,转动一周需要360秒, 若现在你坐在坐在座舱中,从初始位置OA出发(如图所示),过了30秒后,你离地面的高度h为多少?过了45秒呢?所以很自然得到“过了30秒后,过了45秒,你离地面的高度h为:若想做到这一点,就得把锐角的正弦推广到任意角的正弦. 问题5:
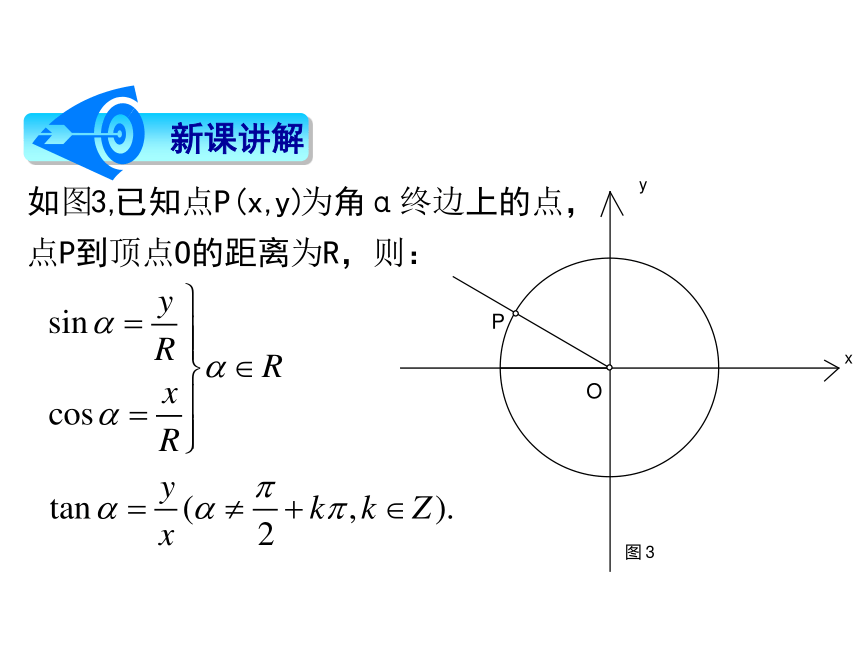
改变终边上的点的位置,这三个比值会改变吗?
为什么? 回答:不会改变问题6:
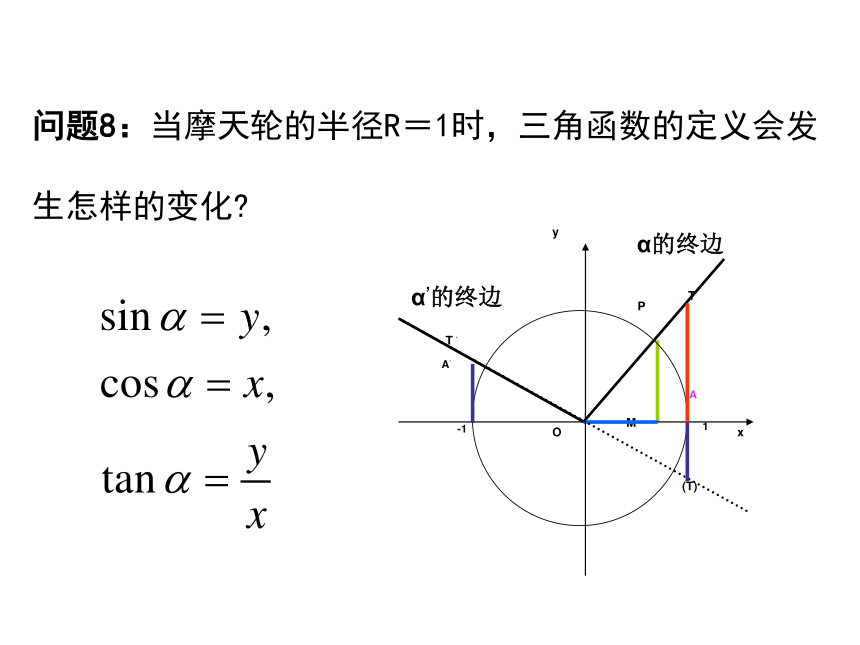
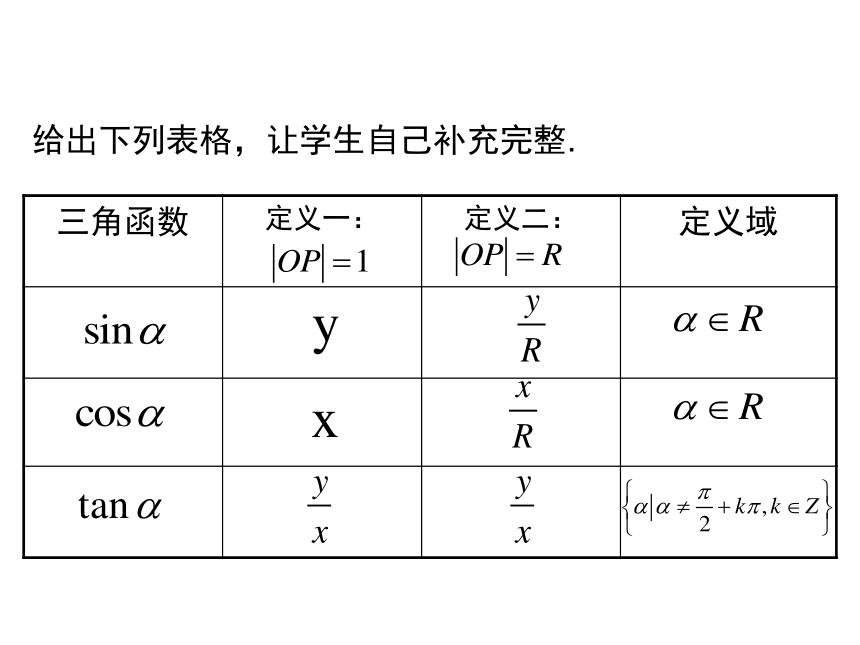
大家根据第一象限角的正弦函数的定义,能否也给出第二象限角的定义呢? 问题8:当摩天轮的半径R=1时,三角函数的定义会发生怎样的变化? 给出下列表格,让学生自己补充完整.练习2. 通过观察摩天轮的旋转,三角函数的角的终边所在象限不同,请说说三角函数在各个象限内的三角函数值的符号?独立完成课本P15的“探究”. 作业:P20习题1.2A组 1,2,3
1.2.1 任意角的三角函数(2)复习: 任意角的三角函数的有关概念2.利用定义探究三角函数的定义域,函数值的符号探究:请根据任意角的三角函数定义,将正弦、余弦和正切函数在弧度制下的定义域填入表格;再将这三种函数的值在各个象限的符号填入表格中:(课本13页) 由三角函数的定义,以及各象限内点的坐标的符号,我们可以得知: 思考:根据三角函数的定义,终边相同的角的同一三角函数值有何关系? 终边相同的角的同一三角函数值相等. 注意:公式一的作用是把任意角的三角函数值问题转化为0~2π间角的三角函数值问题. 例2. 确定下列三角函数值的符号: 解析:(1)负 (2)负 (3)正 (4)负作业:(1)P15 练习
(2)P17 练习
(3)P20 习题1.2 A组 6、7、8、9 1.2.2 同角三角函数的基本关系 大家都听过一句话:南美洲亚马逊河雨林中的一只蝴蝶,偶尔扇动几下翅膀,可能在两周后引起美国德克萨斯州的一场龙卷风.这就是著名的“蝴蝶效应”,他本意是说事物初始条件的微弱变化可能会引起结果的巨大变化. 两个似乎毫不相干的事物,却有着这样的联系.那么我们来看看前些天我们所学习的三角函数.在三个式子中有着“同一个角”其中的联系应该更为紧密! 西方有一句著名的民谣:
丢失一个钉子,坏了一只蹄铁;
坏了一只蹄铁,折了一匹战马;
折了一匹战马,伤了一位骑士;
伤了一位骑士,输了一场战斗;
输了一场战斗,亡了一个帝国. 请你写出几个特殊角的三角函数值,观察他们之间的关系,猜想之间的联系.问题1:从以上的过程中,你能发现什么一般规律?问题2:你能否用代数式表示这两个规律?注意:思考1:你能将两个公式变形么?思考2:判断下列等式是否成立: √√√╳╳√注意:对于不知道α是第几象限角的情况,采用“符号看象限”及分类讨论的思想来处理.是否还有其他的证明方法证明三角恒等式经常使用的方法:
1:从等式左边变形到右边;
2:从恒等式出发,转化到所要证明的等式上;
3:左边减去右边等于0;
4:左边除以右边等于1(保证分母不为零). (1)通过本节课的学习,你学会了哪两个公式?
(2)学会了运用两个公式去处理什么类型的问题?
(3)在解决遇见的两类问题时,应分别注意哪些方面的要点?
(4)你能总结本节课的知识体系么? 一:书中P20页练习题1、2、4、5
二:探究题:已知tanα为非零实数,用tanα表示sinα,cosα.
三:研究性学习:利用周末时间,查找课外资料,了解同角三角函数的其他几个基本关系.
改变终边上的点的位置,这三个比值会改变吗?
为什么? 回答:不会改变问题6:
大家根据第一象限角的正弦函数的定义,能否也给出第二象限角的定义呢? 问题8:当摩天轮的半径R=1时,三角函数的定义会发生怎样的变化? 给出下列表格,让学生自己补充完整.练习2. 通过观察摩天轮的旋转,三角函数的角的终边所在象限不同,请说说三角函数在各个象限内的三角函数值的符号?独立完成课本P15的“探究”. 作业:P20习题1.2A组 1,2,3
1.2.1 任意角的三角函数(2)复习: 任意角的三角函数的有关概念2.利用定义探究三角函数的定义域,函数值的符号探究:请根据任意角的三角函数定义,将正弦、余弦和正切函数在弧度制下的定义域填入表格;再将这三种函数的值在各个象限的符号填入表格中:(课本13页) 由三角函数的定义,以及各象限内点的坐标的符号,我们可以得知: 思考:根据三角函数的定义,终边相同的角的同一三角函数值有何关系? 终边相同的角的同一三角函数值相等. 注意:公式一的作用是把任意角的三角函数值问题转化为0~2π间角的三角函数值问题. 例2. 确定下列三角函数值的符号: 解析:(1)负 (2)负 (3)正 (4)负作业:(1)P15 练习
(2)P17 练习
(3)P20 习题1.2 A组 6、7、8、9 1.2.2 同角三角函数的基本关系 大家都听过一句话:南美洲亚马逊河雨林中的一只蝴蝶,偶尔扇动几下翅膀,可能在两周后引起美国德克萨斯州的一场龙卷风.这就是著名的“蝴蝶效应”,他本意是说事物初始条件的微弱变化可能会引起结果的巨大变化. 两个似乎毫不相干的事物,却有着这样的联系.那么我们来看看前些天我们所学习的三角函数.在三个式子中有着“同一个角”其中的联系应该更为紧密! 西方有一句著名的民谣:
丢失一个钉子,坏了一只蹄铁;
坏了一只蹄铁,折了一匹战马;
折了一匹战马,伤了一位骑士;
伤了一位骑士,输了一场战斗;
输了一场战斗,亡了一个帝国. 请你写出几个特殊角的三角函数值,观察他们之间的关系,猜想之间的联系.问题1:从以上的过程中,你能发现什么一般规律?问题2:你能否用代数式表示这两个规律?注意:思考1:你能将两个公式变形么?思考2:判断下列等式是否成立: √√√╳╳√注意:对于不知道α是第几象限角的情况,采用“符号看象限”及分类讨论的思想来处理.是否还有其他的证明方法证明三角恒等式经常使用的方法:
1:从等式左边变形到右边;
2:从恒等式出发,转化到所要证明的等式上;
3:左边减去右边等于0;
4:左边除以右边等于1(保证分母不为零). (1)通过本节课的学习,你学会了哪两个公式?
(2)学会了运用两个公式去处理什么类型的问题?
(3)在解决遇见的两类问题时,应分别注意哪些方面的要点?
(4)你能总结本节课的知识体系么? 一:书中P20页练习题1、2、4、5
二:探究题:已知tanα为非零实数,用tanα表示sinα,cosα.
三:研究性学习:利用周末时间,查找课外资料,了解同角三角函数的其他几个基本关系.
