数学高中必修四苏教版1.3《三角函数的图象与性质》课件
文档属性
| 名称 | 数学高中必修四苏教版1.3《三角函数的图象与性质》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 173.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-04 20:55:40 | ||
图片预览

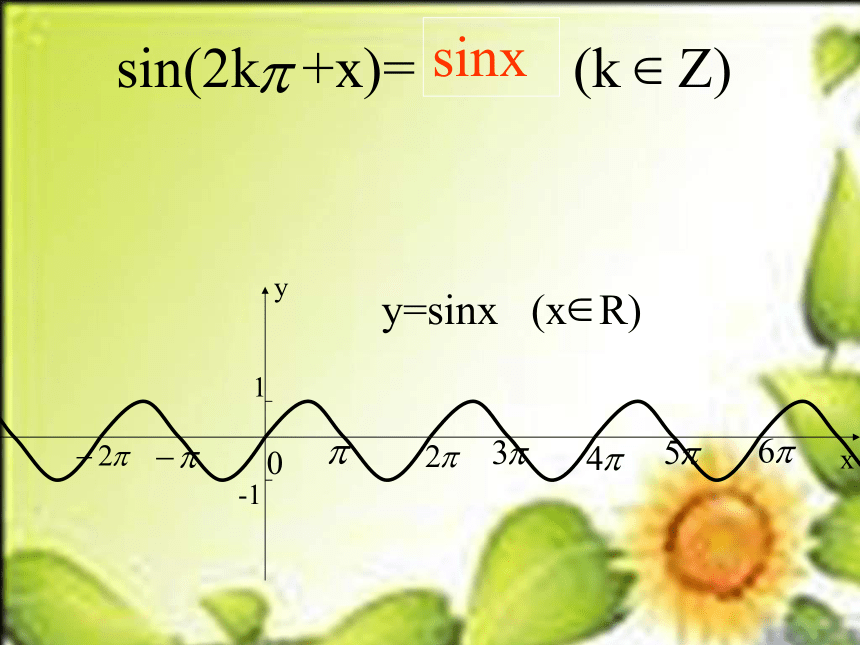

文档简介
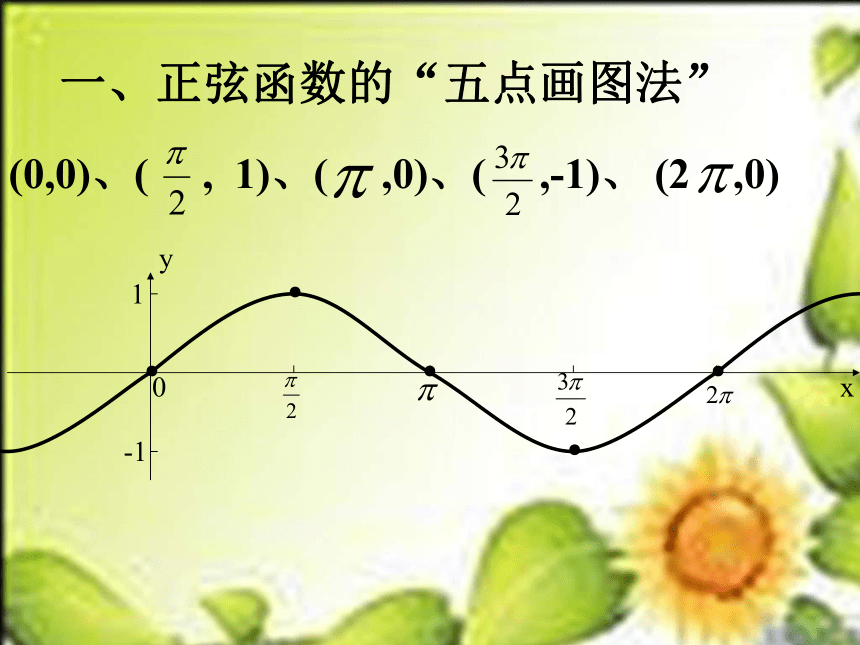
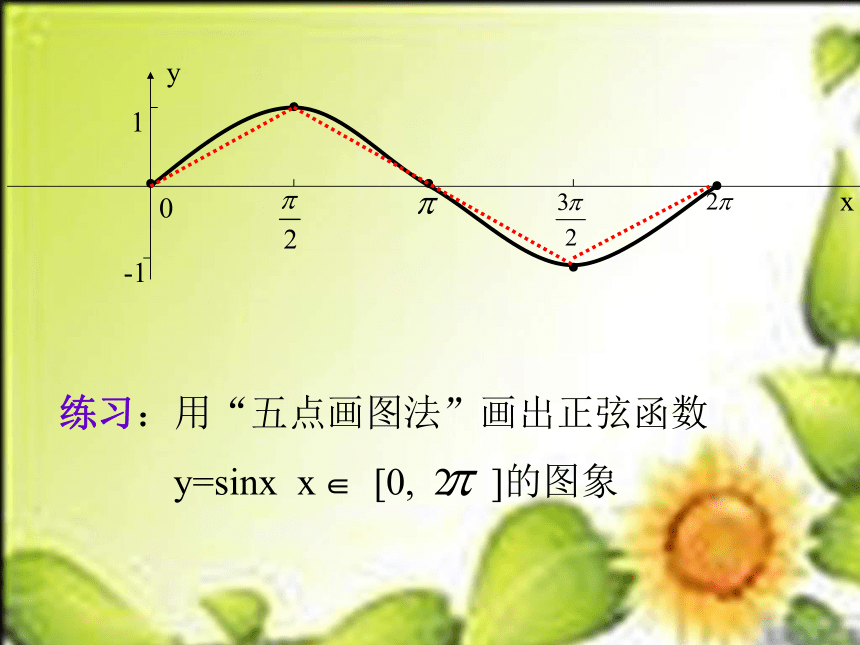
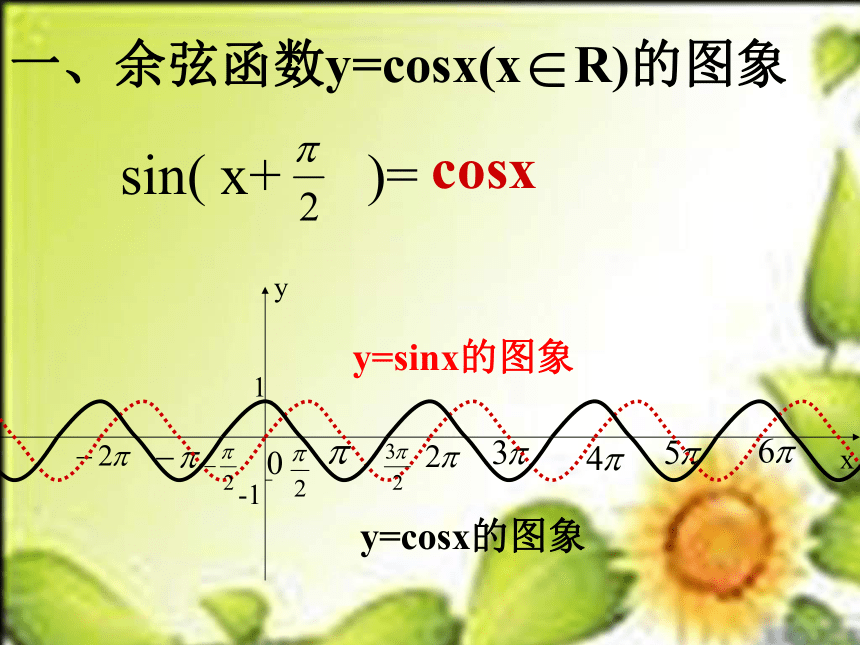
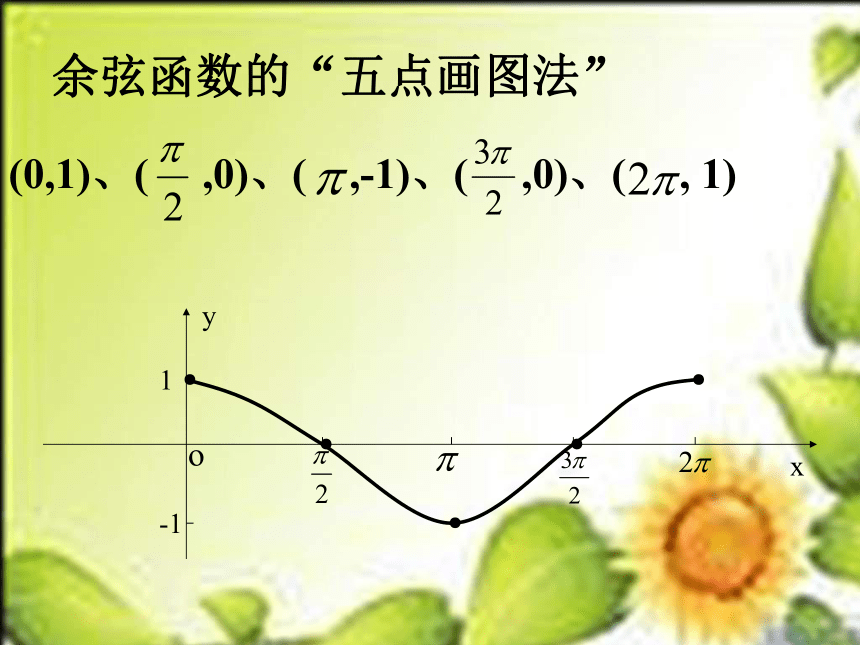
课件14张PPT。----正弦、余弦函数图象三角函数图象和性质 sin(2k +x)= (k Z)sinxxy01-1 y=sinx (x R) 一、正弦函数的“五点画图法”(0,0)、( , 1)、( ,0)、( ,-1)、 (2 ,0)0xy1-1●●●●●0xy1-1●●●●●xy01-1 sin( x+ )=一、余弦函数y=cosx(x R)的图象cosxy=sinx的图象y=cosx的图象余弦函数的“五点画图法”(0,1)、( ,0)、( ,-1)、( ,0)、( , 1)oxy●●●●●1-1例:画出下列函数的简图
(1)y=1+sinx, x [0, ]
(2)y= - cosx, x [0, ]解:(1)按五个关键点列表:y=1+sinx x∈[0,2π]
xsinx1+sinx0 0 1 0 -1 0 1 2 1 0 1oxy12●●●●●y=1+sinx x [0, ] (2)按五个关键点列表xcosx -cosx0 1 0 -1 0 1 -1 0 1 0 -1oxy1●●●●●y=-cosx x [0, ]-1思考:
1、函数y=1+sinx的图象与函数y=sinx的图象有什么关系?
2、函数y=-cosx的图象与函数y=cosx的图象有什么关系?o-112y=sinx x [0, ]y=1+sinx x [0, ] yxyxo-11y=cosx x [0, ]y=-cosx x [0, ]小结:正弦函数、余弦函数图象的五点法练习:(1)画出函数y=-sinx x∈ [0,2π]
(2)画出函数y=1+cosx x∈ [0,2π]
(3)画出函数y=2sinx x∈ [0,2π]1-1y= -sinx, x [0, ]12y=1+cosx, x [0, ](1)(2)xxyy(3)21-1-2yxy=2sinx, x [0, ]
(1)y=1+sinx, x [0, ]
(2)y= - cosx, x [0, ]解:(1)按五个关键点列表:y=1+sinx x∈[0,2π]
xsinx1+sinx0 0 1 0 -1 0 1 2 1 0 1oxy12●●●●●y=1+sinx x [0, ] (2)按五个关键点列表xcosx -cosx0 1 0 -1 0 1 -1 0 1 0 -1oxy1●●●●●y=-cosx x [0, ]-1思考:
1、函数y=1+sinx的图象与函数y=sinx的图象有什么关系?
2、函数y=-cosx的图象与函数y=cosx的图象有什么关系?o-112y=sinx x [0, ]y=1+sinx x [0, ] yxyxo-11y=cosx x [0, ]y=-cosx x [0, ]小结:正弦函数、余弦函数图象的五点法练习:(1)画出函数y=-sinx x∈ [0,2π]
(2)画出函数y=1+cosx x∈ [0,2π]
(3)画出函数y=2sinx x∈ [0,2π]1-1y= -sinx, x [0, ]12y=1+cosx, x [0, ](1)(2)xxyy(3)21-1-2yxy=2sinx, x [0, ]
