数学高中必修四苏教版2.1《向量的概念与表示》课件1
文档属性
| 名称 | 数学高中必修四苏教版2.1《向量的概念与表示》课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 381.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-04 21:00:43 | ||
图片预览




文档简介
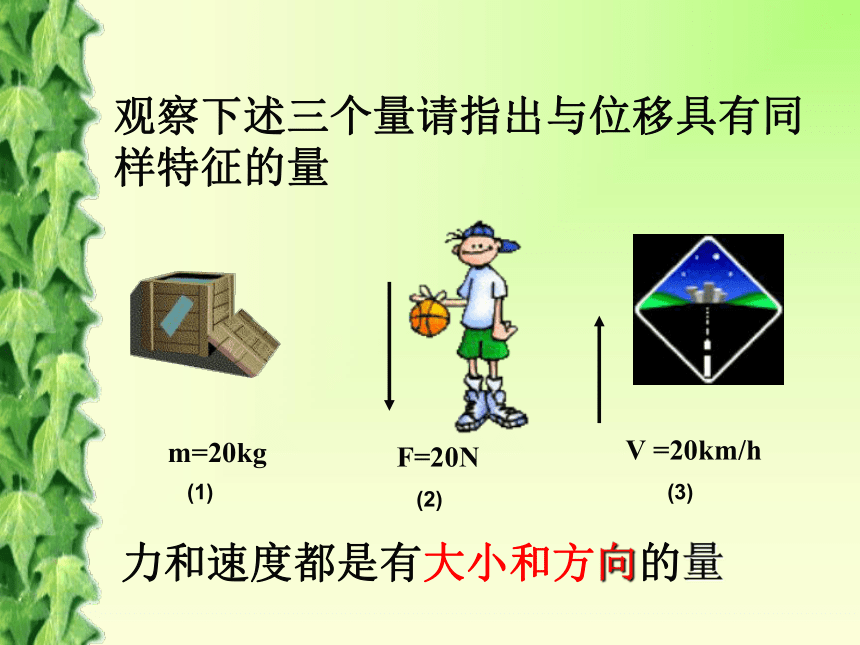
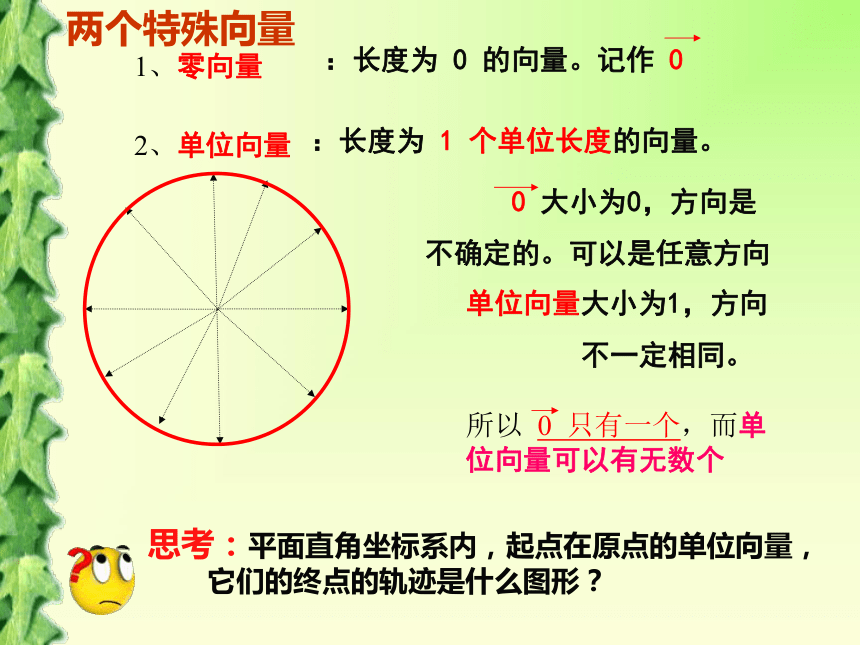
课件27张PPT。Welcome平面向量的实际背景及基本概念日本部署“爱国者-3”型拦截导弹拟拦截可能落入日本境内的朝鲜发射物。新华网东京3月30日电:目标不考虑其他因素,导弹击中拦截目标取决于导弹运行的路程还是位移?F=20NV =20km/h 力和速度都是有大小和方向的量m=20kg(1)(2)(3)观察下述三个量请指出与位移具有同样特征的量既有大小又有方向的量叫做向量注意:向量不能比较大小一、向量的基本概念只有大小没有方向的量叫做数量二、向量的表示方法①几何表示——向量常用有向线段表示:有向线段的 长度表示向量的大小,箭头所指的方向表示向量的方向。1、零向量2、单位向量单位向量大小为1,方向
不一定相同。:长度为 1 个单位长度的向量。两个特殊向量思考:平面直角坐标系内,起点在原点的单位向量,
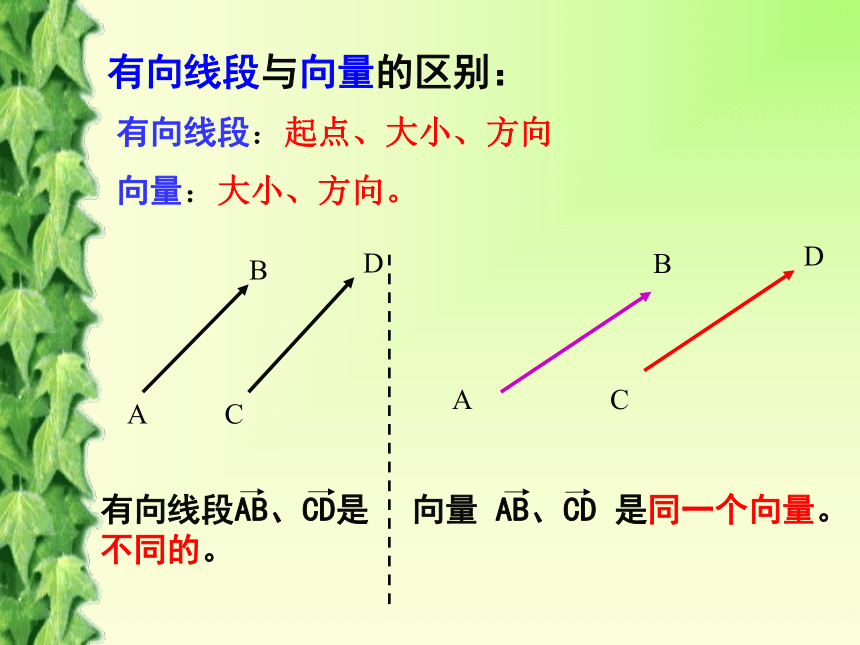
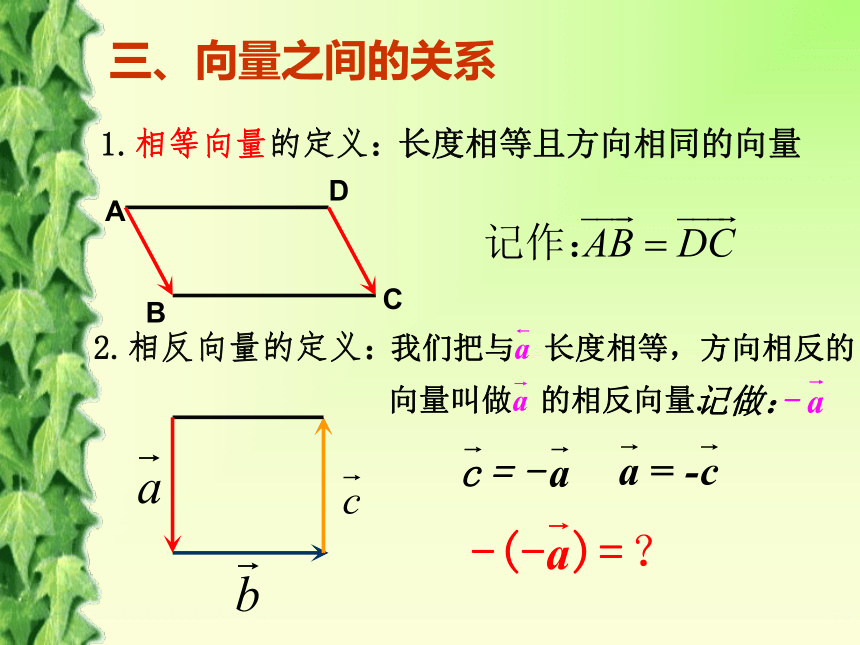
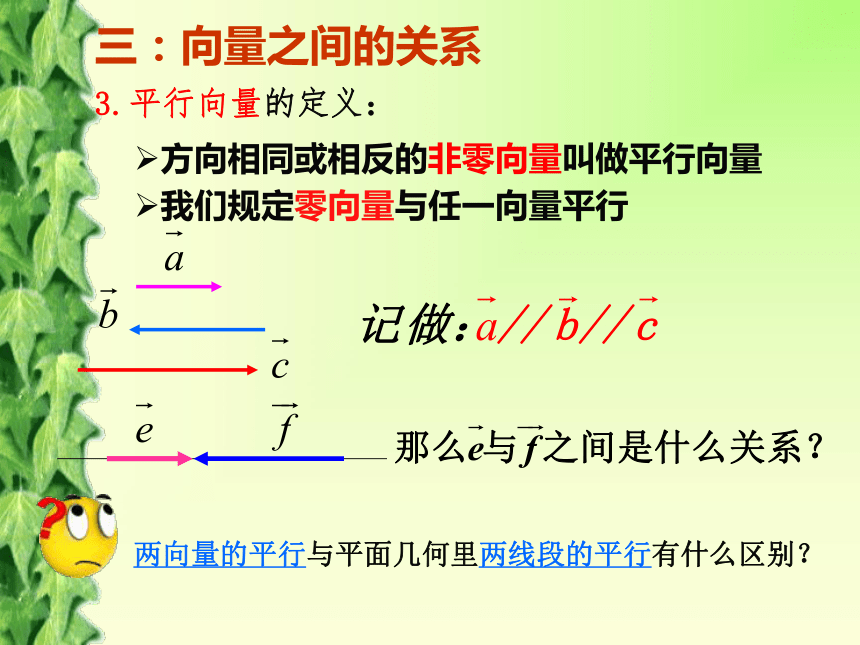
它们的终点的轨迹是什么图形?有向线段与向量的区别:有向线段:起点、大小、方向向量:大小、方向。1.相等向量的定义:长度相等且方向相同的向量2.相反向量的定义:三、向量之间的关系三:向量之间的关系3.平行向量的定义:方向相同或相反的非零向量叫做平行向量我们规定零向量与任一向量平行两向量的平行与平面几何里两线段的平行有什么区别?任意一组平行向量都可以平移到同一直线上三:向量之间的关系3.共线向量与平行向量的关系:平行向量就是共线向量两向量的共线与平面几何里两线段的共线是否一样?
为什么?说明:在平行向量、共线向量、相等向量的概念中应注意零向量的特殊性例1:已知O为正六边形ABCDEF的中心,
在图中所标出的向量中:解:分别以图中的格点为起点和终点作向量,★题:★★★题:★★题:欢迎来到:过关竞技场练习:
1、单位向量是否一定相等?
2、单位向量的大小是否一定相等?BACK不一定一定练习:
3、平行向量是否一定方向相同?
4、不相等的向量一定不平行吗?BACK不一定不一定BACK练习
5、与零向量相等的向量一定是什么向量?
6、与任意向量都平行的向量是什么向量?零向量零向量BACK练习
7、若两个向量在同一直线上,则这两个
向量是什么向量?
8、共线向量一定在一条直线上吗?共线向量 或者说平行向量不一定9.在下列结论中,哪些是正确的?
(1)如果两个向量相等,那么它们的起点和终
点分别重合;
(2)模相等的两个平行向量是相等的向量;
(3)如果两个向量是单位向量,那么它们相等;
(4)两个相等向量的模相等。正确的有:(4)练习:
10.设O为正△ABC的中心,则向量AO,BO,CO是 ( )
A.相等向量 B.模相等的向量
C.共线向量 D.共起点的向量
BABCOBACK练习:
命题:“│a│=│b│”成立,则“ a = b ”一定成
立×BACK练习:
12.已知a、b为不共线的非零向量,且
存在向量 c,使 c ∥ a, c ∥ b, 则
c =____BACK练习:
13.与非零向量 a 平行的向量中,
不相等的单位向量有_____个.2 练习:如图,EF是△ABC的中位线,AD是BC 边上的中 线,在以A、B、C、D、E、F为端点的有向线
段表示的向量中请分别写出
(1)与向量CD共线的向量有___个,
分别是______________________;
(2)与向量DF的模一定相等的向
量有__个,分别是_________________;
(3)与向量DE相等的向量有__个,
分别是___________。 ABCDEFBACK752如图,D、E、F分别是△ABC各边上的中点,四边形BCMF是平行四边形,请分别写出:
(1)与ED相等的向量;
(2)与ED共线的向量;
(3)与FE相等的向量;
(4)与FE共线的向量。ABCDFEMBACK(1) 3个(2) 9个(3) 3个(4) 11个课堂小结课后作业:
P77 1、2、3再见
不一定相同。:长度为 1 个单位长度的向量。两个特殊向量思考:平面直角坐标系内,起点在原点的单位向量,
它们的终点的轨迹是什么图形?有向线段与向量的区别:有向线段:起点、大小、方向向量:大小、方向。1.相等向量的定义:长度相等且方向相同的向量2.相反向量的定义:三、向量之间的关系三:向量之间的关系3.平行向量的定义:方向相同或相反的非零向量叫做平行向量我们规定零向量与任一向量平行两向量的平行与平面几何里两线段的平行有什么区别?任意一组平行向量都可以平移到同一直线上三:向量之间的关系3.共线向量与平行向量的关系:平行向量就是共线向量两向量的共线与平面几何里两线段的共线是否一样?
为什么?说明:在平行向量、共线向量、相等向量的概念中应注意零向量的特殊性例1:已知O为正六边形ABCDEF的中心,
在图中所标出的向量中:解:分别以图中的格点为起点和终点作向量,★题:★★★题:★★题:欢迎来到:过关竞技场练习:
1、单位向量是否一定相等?
2、单位向量的大小是否一定相等?BACK不一定一定练习:
3、平行向量是否一定方向相同?
4、不相等的向量一定不平行吗?BACK不一定不一定BACK练习
5、与零向量相等的向量一定是什么向量?
6、与任意向量都平行的向量是什么向量?零向量零向量BACK练习
7、若两个向量在同一直线上,则这两个
向量是什么向量?
8、共线向量一定在一条直线上吗?共线向量 或者说平行向量不一定9.在下列结论中,哪些是正确的?
(1)如果两个向量相等,那么它们的起点和终
点分别重合;
(2)模相等的两个平行向量是相等的向量;
(3)如果两个向量是单位向量,那么它们相等;
(4)两个相等向量的模相等。正确的有:(4)练习:
10.设O为正△ABC的中心,则向量AO,BO,CO是 ( )
A.相等向量 B.模相等的向量
C.共线向量 D.共起点的向量
BABCOBACK练习:
命题:“│a│=│b│”成立,则“ a = b ”一定成
立×BACK练习:
12.已知a、b为不共线的非零向量,且
存在向量 c,使 c ∥ a, c ∥ b, 则
c =____BACK练习:
13.与非零向量 a 平行的向量中,
不相等的单位向量有_____个.2 练习:如图,EF是△ABC的中位线,AD是BC 边上的中 线,在以A、B、C、D、E、F为端点的有向线
段表示的向量中请分别写出
(1)与向量CD共线的向量有___个,
分别是______________________;
(2)与向量DF的模一定相等的向
量有__个,分别是_________________;
(3)与向量DE相等的向量有__个,
分别是___________。 ABCDEFBACK752如图,D、E、F分别是△ABC各边上的中点,四边形BCMF是平行四边形,请分别写出:
(1)与ED相等的向量;
(2)与ED共线的向量;
(3)与FE相等的向量;
(4)与FE共线的向量。ABCDFEMBACK(1) 3个(2) 9个(3) 3个(4) 11个课堂小结课后作业:
P77 1、2、3再见
