数学高中必修四苏教版2.3《向量的坐标表示》课件
文档属性
| 名称 | 数学高中必修四苏教版2.3《向量的坐标表示》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 384.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-04 21:10:40 | ||
图片预览








文档简介
课件23张PPT。2.3.3平面向量的坐标运算
三维目标
1.通过经历探究活动,使学生掌握平面向量的和、差、实数与向量的积的坐标表示方法。理解并掌握平面向量的坐标运算。
2.引入平面向量的坐标可使向量运算完全代数化,平面向量的坐标成了数与形结合的载体。
3.在解决问题过程中要形成见数思形、以形助数的思维习惯,以加深理解知识要点,增强应用意识。重点难点
教学重点:平面向量的坐标运算
教学难点:平面坐标运算的应用
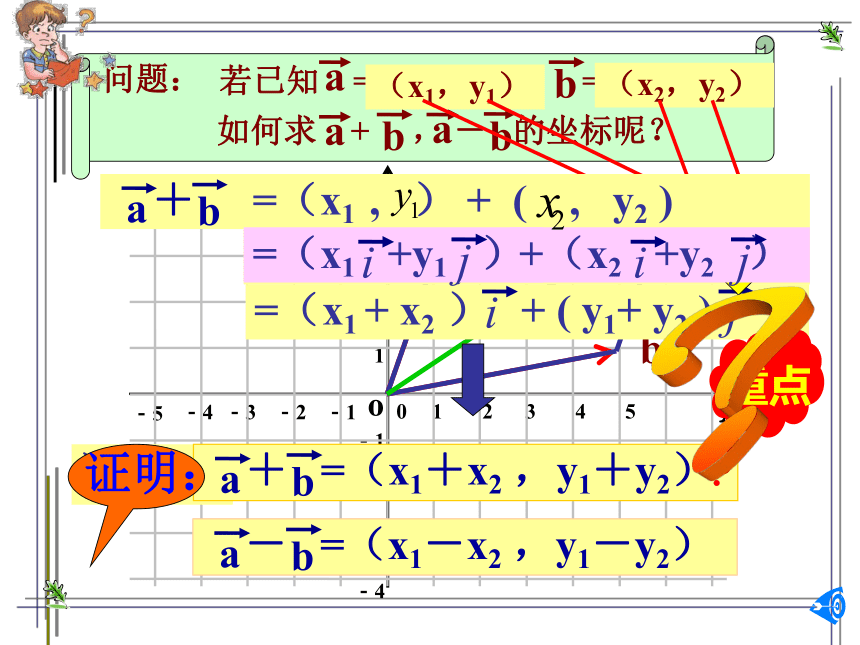
课时安排:1课时问题:若已知 =(1 ,3) , =(5 ,1), (6,4)猜想:=(x1 , ) + ( , y2 ) ?平面向量的坐标运算法则结论:两个向量和(差)的坐标分别等于这两个向量
相应坐标的和(差)。 向量的数乘运算 可别忘了还有“我”呦!?结论:实数与向量的积的坐标等于这个实数乘原来向量的相应坐标平面向量的坐标运算法则重点例(-1,5)(5,-3)(-6,19)(3,-1)(x1,y1)(x2,y2) 例2
已知A、B两点的坐标,求 ,
的坐标。
⑴ A (3,5) , B (6,9) ; ⑵ A(-3,4) , B(6,3)
⑶ A (0,3) , B (0,5) ; ⑷ A (3,0), B(8,0)注意!终点B始点A终点坐标减去始点坐标 ( -2 , 7 )终点坐标减去向量坐标始点坐标加上向量坐标 ( 3 , -4 ) ( 1,3 )( 1,2 )( 2,3 )( 1,1 )例3.如图,已知 四边形 的四个顶点A、B、C,D的坐标分别是(-2,1)、(-1,3)、(3,4),(2,2)求证四边形 ABCD是平行四边形 xy-1-1-2-5-66例3.如图,已知 四边形 的四个顶点A、B、C,D的坐标分别是(-2,1)、(-1,3)、(3,4),(2,2)求证四边形 ABCD是平行四边形 xy-1-1-2-5-66解:设点D的坐标为(x,y)解得 x=2,y=2所以顶点D的坐标为(2,2)另解:由平行四边形法则可得而所以顶点D的坐标为(2,2)思考2:若已知平面上三个点A、B、C 的坐标分别为(-2,1),(-1,3),(3,4),求第四个点的坐标,使这四个点构成一个平行四边形的四个顶点.xy-1-1-2-5-66D请回顾本堂课的教学过程,你能说说你学了哪些知识吗?1.平面向量坐标的加.减运算法则 =( x1 , y1) + (x2 ,? y2)= (x1+x2 , y1+y2)=( x1 , y1) - (x2 ,? y2)= (x1- x2 , y1-y2)2.平面向量坐标实数与向量相乘的运算法则3.平面向量坐标若A(x1 , y1) , B(x2 , y2)则 =(x2 - x1 , y2 – y1 ) =( x1 , y1) + (x2 ,? y2)= (x1+x2 , y1+y2)作业P101 3.7课后反思:
1.通过经历探究活动,使学生掌握平面向量的和、差、实数与向量的积的坐标表示方法。理解并掌握平面向量的坐标运算。
2.引入平面向量的坐标可使向量运算完全代数化,平面向量的坐标成了数与形结合的载体。
3.在解决问题过程中要形成见数思形、以形助数的思维习惯,以加深理解知识要点,增强应用意识。重点难点
教学重点:平面向量的坐标运算
教学难点:平面坐标运算的应用
课时安排:1课时问题:若已知 =(1 ,3) , =(5 ,1), (6,4)猜想:=(x1 , ) + ( , y2 ) ?平面向量的坐标运算法则结论:两个向量和(差)的坐标分别等于这两个向量
相应坐标的和(差)。 向量的数乘运算 可别忘了还有“我”呦!?结论:实数与向量的积的坐标等于这个实数乘原来向量的相应坐标平面向量的坐标运算法则重点例(-1,5)(5,-3)(-6,19)(3,-1)(x1,y1)(x2,y2) 例2
已知A、B两点的坐标,求 ,
的坐标。
⑴ A (3,5) , B (6,9) ; ⑵ A(-3,4) , B(6,3)
⑶ A (0,3) , B (0,5) ; ⑷ A (3,0), B(8,0)注意!终点B始点A终点坐标减去始点坐标 ( -2 , 7 )终点坐标减去向量坐标始点坐标加上向量坐标 ( 3 , -4 ) ( 1,3 )( 1,2 )( 2,3 )( 1,1 )例3.如图,已知 四边形 的四个顶点A、B、C,D的坐标分别是(-2,1)、(-1,3)、(3,4),(2,2)求证四边形 ABCD是平行四边形 xy-1-1-2-5-66例3.如图,已知 四边形 的四个顶点A、B、C,D的坐标分别是(-2,1)、(-1,3)、(3,4),(2,2)求证四边形 ABCD是平行四边形 xy-1-1-2-5-66解:设点D的坐标为(x,y)解得 x=2,y=2所以顶点D的坐标为(2,2)另解:由平行四边形法则可得而所以顶点D的坐标为(2,2)思考2:若已知平面上三个点A、B、C 的坐标分别为(-2,1),(-1,3),(3,4),求第四个点的坐标,使这四个点构成一个平行四边形的四个顶点.xy-1-1-2-5-66D请回顾本堂课的教学过程,你能说说你学了哪些知识吗?1.平面向量坐标的加.减运算法则 =( x1 , y1) + (x2 ,? y2)= (x1+x2 , y1+y2)=( x1 , y1) - (x2 ,? y2)= (x1- x2 , y1-y2)2.平面向量坐标实数与向量相乘的运算法则3.平面向量坐标若A(x1 , y1) , B(x2 , y2)则 =(x2 - x1 , y2 – y1 ) =( x1 , y1) + (x2 ,? y2)= (x1+x2 , y1+y2)作业P101 3.7课后反思:
