数学北师大版(2019)必修第二册 1.3..1弧度概念132弧度与角度的换算 课件(29张ppt)
文档属性
| 名称 | 数学北师大版(2019)必修第二册 1.3..1弧度概念132弧度与角度的换算 课件(29张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 719.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-22 15:51:50 | ||
图片预览








文档简介
(共29张PPT)
1.3.1 弧度概念
1.3.2 弧度与角度的换算
课标阐释
1.理解弧度的意义,掌握1弧度的角的定义.(数学抽象)
2.能进行角度和弧度的换算,熟记特殊角的弧度数.(数学运算)
3.掌握弧度制下扇形的弧长和面积公式,会利用弧度解决某些简单的实际问题.(数学建模)
4.通过学习,要理解角度制与弧度制都是度量角的方法,二者是辩证统一的.(逻辑推理)
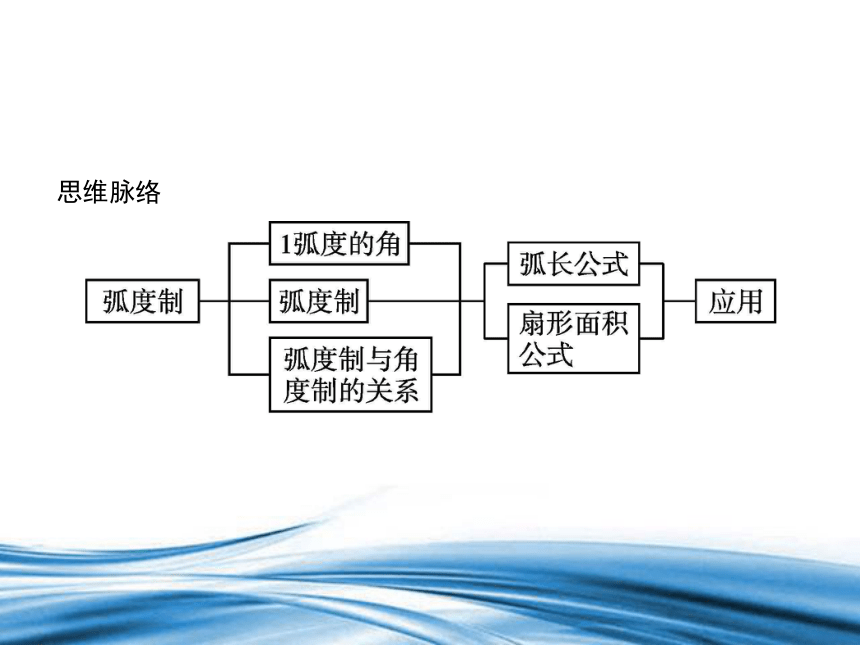
思维脉络
激趣诱思
知识点拨
测量一位同学的身高,可以用米、分米、厘米为单位进行度量;买一个西瓜,要称其重量,常用的单位有千克、克.在物理学和日常生活中,一个量常常需要用不同的方法进行度量,不同的度量方法可以满足我们不同的需要.现实生活中有许多计量单位,如度量长度可以用米、厘米、尺、码等不同的单位,度量重量可以用千克、克、吨等不同的单位,度量角的大小可以用哪些单位呢
激趣诱思
知识点拨
一、弧度
在单位圆中,把长度等于1的弧所对的圆心角称为1弧度的角.其单位用符号rad表示,读作弧度.
名师点析1.1弧度的角与1度的角所指含义不同,大小更不同.
2.无论是以“弧度”还是以“度”为单位来度量角,角的大小与“半径”大小无关.
3.用“度”作为单位度量角时,“度”(即“°”)不能省略,而用“弧度”作为单位度量角时,“弧度”二字或“rad”通常省略不写.
激趣诱思
知识点拨
微判断
判断(正确的打“√”,错误的打“×”).
(1)大圆中1弧度的角比小圆中1弧度的角大.( )
(2)圆心角为1弧度的扇形的弧长都相等.( )
(3)“度”和“弧度”是度量角的两种不同的度量单位.( )
答案(1)× (2)× (3)√
激趣诱思
知识点拨
二、弧度制
在单位圆中,每一段弧的长度就是它所对圆心角的弧度数.这种以弧度作为单位来度量角的方法,称作弧度制.
名师点析1.当圆心角一定时,它所对的弧长与半径的比值是唯一一个确定的值,与所取圆的半径大小无关.
2.一般地,弧度与实数一一对应,正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0.
微思考
在同一个表达式中,能不能角度制和弧度制同时出现
提示角度制和弧度制是表示角的两种不同的度量方法,两者有着本质的不同,因此在同一个表达式中两种度量方法不能混用.
激趣诱思
知识点拨
三、弧度与角度的换算
名师点析一些特殊角的度数与弧度数的对应值表
激趣诱思
知识点拨
微思考1
周角是多少度 是多少弧度
提示360°,2π.
微思考2
半圆所对的圆心角是多少度 是多少弧度
提示180°,π.
微练习
激趣诱思
知识点拨
四、弧度制下的三个公式
激趣诱思
知识点拨
名师点析扇形的弧长及面积公式的记忆
激趣诱思
知识点拨
微练习
已知扇形的半径r=30,圆心角 ,则该扇形的弧长等于 ,面积等于 ,周长等于 .
答案5π 75π 60+5π
探究一
探究二
探究三
探究四
当堂检测
弧度制的概念
例1下列说法错误的是( )
A.弧度角与实数之间建立了一一对应的关系
C.根据弧度的定义,180°一定等于π弧度
D.无论是用角度制还是用弧度制度量角,角的大小均与圆的半径的大小有关
解析无论是用角度制还是用弧度制度量角,角的大小均与圆的半径大小无关,而是与弧长和半径的比值有关,故D项错误.
答案D
探究一
探究二
探究三
探究四
当堂检测
反思感悟 弧度制与角度制的异同
1.用角度制和弧度制度量零角时,单位不同,但数值相同(都是0);用角度制和弧度制度量任一非零角时,单位不同,数值也不同.
2.以弧度为单位表示角的大小时,“弧度”二字或“rad”通常省略不写,但以度为单位表示角的大小时,“度”或“°”不能省略.
探究一
探究二
探究三
探究四
当堂检测
变式训练1下列叙述中正确的是( )
A.1弧度是1度的圆心角所对的弧
B.1弧度是长度为半径的弧
C.1弧度是1度的弧与1度的角之和
D.1弧度是长度等于半径长的弧所对的圆心角的大小,它是角的一种度量单位
解析弧度是度量角的大小的一种单位,1弧度是长度等于半径的圆弧所对圆心角的大小.故选D.
答案D
探究一
探究二
探究三
探究四
当堂检测
弧度与角度的换算
例2(1)把112°30'化成弧度;
(3)将-1 485°化成弧度.
探究一
探究二
探究三
探究四
当堂检测
反思感悟 弧度制与角度制换算的关键与方法
(1)关键:抓住互化公式π rad=180°.
(3)角度化弧度时,应先将分、秒化成度,再化成弧度.
探究一
探究二
探究三
探究四
当堂检测
变式训练2下列各角中,与240°角终边相同的角为( )
探究一
探究二
探究三
探究四
当堂检测
用弧度制表示角及其范围
例3如图所示,用弧度制表示顶点在原点、始边与x轴的非负半轴重合、终边落在阴影部分内的角的集合.
探究一
探究二
探究三
探究四
当堂检测
探究一
探究二
探究三
探究四
当堂检测
反思感悟 用弧度制表示象限角、轴线角、终边相同的角的方法
1.用弧度制表示象限角的集合如下:
2.用弧度制表示轴线角的集合如下:
终边落在x轴上的角为{α|α=kπ,k∈Z);
3.用弧度制表示终边相同的角的集合为{β|β=α+2kπ,k∈Z}.
探究一
探究二
探究三
探究四
当堂检测
变式训练3终边在坐标轴上角的集合是 ,终边在直线y=-x上角的集合是 .
探究一
探究二
探究三
探究四
当堂检测
与扇形弧长、面积有关的问题
例4(1)已知扇形的周长为8 cm,圆心角为2,求该扇形的面积;
(2)已知扇形的周长为10 cm,面积等于4 cm2,求其圆心角的弧度数.
解(1)设扇形的半径为r cm,弧长为l cm,由圆心角为2 rad,依据弧长公式可得l=2r,从而扇形的周长为l+2r=4r=8,解得r=2,则l=4.故扇形的面积
探究一
探究二
探究三
探究四
当堂检测
探究一
探究二
探究三
探究四
当堂检测
反思感悟 弧度制下有关弧长、扇形面积问题的解题策略
(1)扇形的弧长公式和面积公式涉及四个量,即面积S,弧长l,圆心角α,半径r,已知其中的三个量一定能求得第四个量(通过方程求得),已知其中的两个量能求得剩余的两个量(通过方程组求得).
(2)在研究有关扇形的相关量的最值时,往往转化为二次函数的最值问题.
(3)注意扇形圆心角弧度数的取值范围是(0,2π),实际问题中注意根据这一范围进行取舍.
探究一
探究二
探究三
探究四
当堂检测
变式训练4已知扇形的周长是30 cm,当它的半径和圆心角各取什么值时,才能使扇形的面积最大 最大面积是多少
解设扇形的圆心角为α(0<α<2π),半径为r cm,面积为S cm2,弧长为l cm,则l+2r=30,故l=30-2r,
探究一
探究二
探究三
探究四
当堂检测
1.1 920°化为弧度是( )
探究一
探究二
探究三
探究四
当堂检测
答案B
3.若扇形的半径为1,圆心角为3弧度,则扇形的面积为 .
探究一
探究二
探究三
探究四
当堂检测
4.已知两角的和是1弧度,两角的差是1°,则这两个角分别为 .
1.3.1 弧度概念
1.3.2 弧度与角度的换算
课标阐释
1.理解弧度的意义,掌握1弧度的角的定义.(数学抽象)
2.能进行角度和弧度的换算,熟记特殊角的弧度数.(数学运算)
3.掌握弧度制下扇形的弧长和面积公式,会利用弧度解决某些简单的实际问题.(数学建模)
4.通过学习,要理解角度制与弧度制都是度量角的方法,二者是辩证统一的.(逻辑推理)
思维脉络
激趣诱思
知识点拨
测量一位同学的身高,可以用米、分米、厘米为单位进行度量;买一个西瓜,要称其重量,常用的单位有千克、克.在物理学和日常生活中,一个量常常需要用不同的方法进行度量,不同的度量方法可以满足我们不同的需要.现实生活中有许多计量单位,如度量长度可以用米、厘米、尺、码等不同的单位,度量重量可以用千克、克、吨等不同的单位,度量角的大小可以用哪些单位呢
激趣诱思
知识点拨
一、弧度
在单位圆中,把长度等于1的弧所对的圆心角称为1弧度的角.其单位用符号rad表示,读作弧度.
名师点析1.1弧度的角与1度的角所指含义不同,大小更不同.
2.无论是以“弧度”还是以“度”为单位来度量角,角的大小与“半径”大小无关.
3.用“度”作为单位度量角时,“度”(即“°”)不能省略,而用“弧度”作为单位度量角时,“弧度”二字或“rad”通常省略不写.
激趣诱思
知识点拨
微判断
判断(正确的打“√”,错误的打“×”).
(1)大圆中1弧度的角比小圆中1弧度的角大.( )
(2)圆心角为1弧度的扇形的弧长都相等.( )
(3)“度”和“弧度”是度量角的两种不同的度量单位.( )
答案(1)× (2)× (3)√
激趣诱思
知识点拨
二、弧度制
在单位圆中,每一段弧的长度就是它所对圆心角的弧度数.这种以弧度作为单位来度量角的方法,称作弧度制.
名师点析1.当圆心角一定时,它所对的弧长与半径的比值是唯一一个确定的值,与所取圆的半径大小无关.
2.一般地,弧度与实数一一对应,正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0.
微思考
在同一个表达式中,能不能角度制和弧度制同时出现
提示角度制和弧度制是表示角的两种不同的度量方法,两者有着本质的不同,因此在同一个表达式中两种度量方法不能混用.
激趣诱思
知识点拨
三、弧度与角度的换算
名师点析一些特殊角的度数与弧度数的对应值表
激趣诱思
知识点拨
微思考1
周角是多少度 是多少弧度
提示360°,2π.
微思考2
半圆所对的圆心角是多少度 是多少弧度
提示180°,π.
微练习
激趣诱思
知识点拨
四、弧度制下的三个公式
激趣诱思
知识点拨
名师点析扇形的弧长及面积公式的记忆
激趣诱思
知识点拨
微练习
已知扇形的半径r=30,圆心角 ,则该扇形的弧长等于 ,面积等于 ,周长等于 .
答案5π 75π 60+5π
探究一
探究二
探究三
探究四
当堂检测
弧度制的概念
例1下列说法错误的是( )
A.弧度角与实数之间建立了一一对应的关系
C.根据弧度的定义,180°一定等于π弧度
D.无论是用角度制还是用弧度制度量角,角的大小均与圆的半径的大小有关
解析无论是用角度制还是用弧度制度量角,角的大小均与圆的半径大小无关,而是与弧长和半径的比值有关,故D项错误.
答案D
探究一
探究二
探究三
探究四
当堂检测
反思感悟 弧度制与角度制的异同
1.用角度制和弧度制度量零角时,单位不同,但数值相同(都是0);用角度制和弧度制度量任一非零角时,单位不同,数值也不同.
2.以弧度为单位表示角的大小时,“弧度”二字或“rad”通常省略不写,但以度为单位表示角的大小时,“度”或“°”不能省略.
探究一
探究二
探究三
探究四
当堂检测
变式训练1下列叙述中正确的是( )
A.1弧度是1度的圆心角所对的弧
B.1弧度是长度为半径的弧
C.1弧度是1度的弧与1度的角之和
D.1弧度是长度等于半径长的弧所对的圆心角的大小,它是角的一种度量单位
解析弧度是度量角的大小的一种单位,1弧度是长度等于半径的圆弧所对圆心角的大小.故选D.
答案D
探究一
探究二
探究三
探究四
当堂检测
弧度与角度的换算
例2(1)把112°30'化成弧度;
(3)将-1 485°化成弧度.
探究一
探究二
探究三
探究四
当堂检测
反思感悟 弧度制与角度制换算的关键与方法
(1)关键:抓住互化公式π rad=180°.
(3)角度化弧度时,应先将分、秒化成度,再化成弧度.
探究一
探究二
探究三
探究四
当堂检测
变式训练2下列各角中,与240°角终边相同的角为( )
探究一
探究二
探究三
探究四
当堂检测
用弧度制表示角及其范围
例3如图所示,用弧度制表示顶点在原点、始边与x轴的非负半轴重合、终边落在阴影部分内的角的集合.
探究一
探究二
探究三
探究四
当堂检测
探究一
探究二
探究三
探究四
当堂检测
反思感悟 用弧度制表示象限角、轴线角、终边相同的角的方法
1.用弧度制表示象限角的集合如下:
2.用弧度制表示轴线角的集合如下:
终边落在x轴上的角为{α|α=kπ,k∈Z);
3.用弧度制表示终边相同的角的集合为{β|β=α+2kπ,k∈Z}.
探究一
探究二
探究三
探究四
当堂检测
变式训练3终边在坐标轴上角的集合是 ,终边在直线y=-x上角的集合是 .
探究一
探究二
探究三
探究四
当堂检测
与扇形弧长、面积有关的问题
例4(1)已知扇形的周长为8 cm,圆心角为2,求该扇形的面积;
(2)已知扇形的周长为10 cm,面积等于4 cm2,求其圆心角的弧度数.
解(1)设扇形的半径为r cm,弧长为l cm,由圆心角为2 rad,依据弧长公式可得l=2r,从而扇形的周长为l+2r=4r=8,解得r=2,则l=4.故扇形的面积
探究一
探究二
探究三
探究四
当堂检测
探究一
探究二
探究三
探究四
当堂检测
反思感悟 弧度制下有关弧长、扇形面积问题的解题策略
(1)扇形的弧长公式和面积公式涉及四个量,即面积S,弧长l,圆心角α,半径r,已知其中的三个量一定能求得第四个量(通过方程求得),已知其中的两个量能求得剩余的两个量(通过方程组求得).
(2)在研究有关扇形的相关量的最值时,往往转化为二次函数的最值问题.
(3)注意扇形圆心角弧度数的取值范围是(0,2π),实际问题中注意根据这一范围进行取舍.
探究一
探究二
探究三
探究四
当堂检测
变式训练4已知扇形的周长是30 cm,当它的半径和圆心角各取什么值时,才能使扇形的面积最大 最大面积是多少
解设扇形的圆心角为α(0<α<2π),半径为r cm,面积为S cm2,弧长为l cm,则l+2r=30,故l=30-2r,
探究一
探究二
探究三
探究四
当堂检测
1.1 920°化为弧度是( )
探究一
探究二
探究三
探究四
当堂检测
答案B
3.若扇形的半径为1,圆心角为3弧度,则扇形的面积为 .
探究一
探究二
探究三
探究四
当堂检测
4.已知两角的和是1弧度,两角的差是1°,则这两个角分别为 .
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
