数学高中苏教版必修五3.3《二元一次不等式组与简单线性规划》课件
文档属性
| 名称 | 数学高中苏教版必修五3.3《二元一次不等式组与简单线性规划》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 534.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-05 10:36:40 | ||
图片预览










文档简介
课件88张PPT。1. 会从实际情境中抽象出二元一次不等式组.
2.了解二元一次不等式的几何意义,能用平面区域
表示二元一次不等式组.
3.会从实际情境中抽象出一些简单的二元线性规划
问题,并能加以解决.
?3.3 二元一次不等式组与简单的线性规划问题[理 要 点]
一、二元一次不等式表示平面区域
1.二元一次不等式Ax+By+C>0在平面直角坐标系中表示
直线Ax+By+C=0某一侧的所有点组成的平面区域(半平面), 边界直线.
不等式Ax+By+C≥0所表示的平面区域(半平面) 边界直线.
不含包含2.对于直线Ax+By+C=0同一侧的所有点(x,y),使得Ax+By+C的值符号相同,也就是位于同一半平面内的点,其坐标适合 ;而位于另一个半平面内的点,其坐标适合Ax+By+C>0Ax+By+C<03.可在直线Ax+By+C=0的某一侧任取一点,一般取特殊点(x0,y0),从Ax0+By0+C的 来判断Ax+By+C>0(或Ax+By+C<0)所表示的区域.
正负4.由几个不等式组成的不等式组所表示的平面区域,是
各个不等式所表示的平面区域的 .
公共部分二、线性规划中的基本概念不等式(组)
一次解析式一次(x,y)最大值最小值最大值最小值集合?[究 疑 点]
1.可行解与最优解有何关系?最优解是否唯一?
提示:最优解必定是可行解,但可行解不一定是最优解.最优解不一定唯一,有时唯一,有时有多个.
2.点P1(x1,y1)和P2(x2,y2)位于直线Ax+By+C=0的两侧的首要条件是什么?
提示:(Ax1+By1+C)(Ax2+By2+C)<0.
[题组自测]
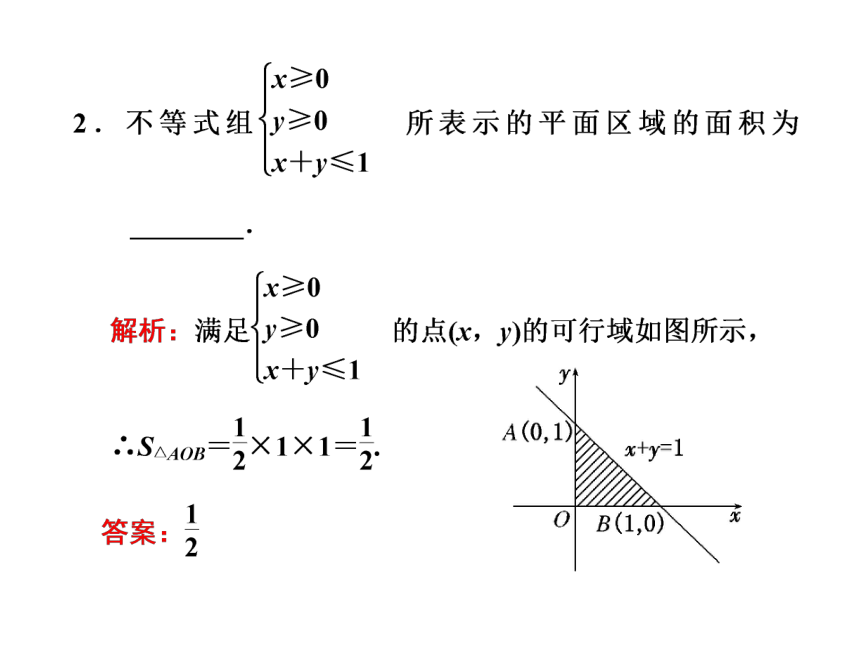
1.如图所示的平面区域(阴影部分)满
足不等式 ( )
A.x+y-1<0
B.x+y-1>0
C.x-y-1<0
D.x-y-1>0答案: B解:(1)先画出直线2x+y-10=0(画成虚线).
取原点(0,0),代入2x+y-10,∵2×0+0-10<0,
∴原点在2x+y-10<0表示的平面区域内,
不等式2x+y-10<0表示的区域如图(1)所示.
(2)不等式x-y+5≥0表示直线x-y+5=0上及右下方的点的集合,x+y+1≥0表示直线x+y+1=0上及右上方的点的集合,x≤3表示直线x=3上及左方的点的集合,所以不等式组表示的平面区域如图(2)所示.
(2)如图,△ABC中,A(0,1),B(-2,2),C(2,6),写出△ABC区域所表示的二元一次不等式组.
答案:(1)A
[归纳领悟]
二元一次不等式(组)表示平面区域的判定方法:
直线定界、特殊点定域.注意不等式是否可取等号,不可取等号时直线画成虚线,可取等号时直线画成实线.若直线不过原点,特殊点常选取原点.答案:A
答案:5
[归纳领悟]
求目标函数的最值的一般步骤是:一画二移三求,其关键是准确作出可行域,准确理解z的几何意义,对于目标函数z=ax+by而言,当b>0时,在可行域内越向上平移直线ax+by=0,z的值越大;越向下平移直线ax+by=0,z的值越小.当b<0时,情况正好相反.[题组自测]
1.一项装修工程需要木工和瓦工共同完成,请木工需付
工资每人50元,请瓦工需付工资每人40元,现有工人工资预算2 000元,设木工x人,瓦工y人,请工人的约束条件是______________.
2.(2010·四川高考)某加工厂用某原料由甲车间加工出A产
品,由乙车间加工出B产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克A产品,每千克A产品获利40元.乙车间加工一箱原料需耗费工时6小时可加工出4千克B产品,每千克B产品获利50元.甲、乙两车间每天共能完成至多70箱原料的加工,每天甲、乙两车间耗费工时总和不得超过480小时,甲、乙两车间每天总获利最大的生产计划为 ( )A.甲车间加工原料10箱,乙车间加工原料60箱
B.甲车间加工原料15箱,乙车间加工原料55箱
C.甲车间加工原料18箱,乙车间加工原料50箱
D.甲车间加工原料40箱,乙车间加工原料30箱
答案:B
3.某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种
玩具共100个,生产一个卫兵需5分钟,生产一个骑兵需7分钟,生产一个伞兵需4分钟,已知总生产时间不超过10小时.若生产一个卫兵可获利润5元,生产一个骑兵可获利润6元,生产一个伞兵可获利润3元.
(1)用每天生产的卫兵个数x与骑兵个数y表示每天的利润w(元);
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
解:(1)依题意每天生产的伞兵个数为100-x-y,所以利润w=5x+6y+3(100-x-y)=2x+3y+300.[归纳领悟]
线性规划实际应用问题的解决常见的错误点有:
(1)不能准确地理解题中条件的含义,如“不超过”、“至
少”等线性约束条件出现失误.
(2)最优解的找法由于作图不规范而不准确.
(3)最大解为“整点时”不会寻找“最优整点解”.处理此类
问题时.一是要规范作图,尤其是边界实虚要分清,二是寻找最优整点解时可记住“整点在整线上”(整线:形如x=k或y=k,k∈Z).
一、把脉考情
从近两年的高考试题来看,二元一次不等式(组)表示的平面区域(的面积)、求目标函数的最值、线性规划的应用问题等是高考的热点,题型既有选择题,也有填空题,难度为中低档题;主要考查平面区域的画法、目标函数最值的求法,以及在取得最值时参数的取值范围.同时注重考查等价转化、数形结合思想.
预测2012年高考仍将以目标函数的最值、线性规划的综合运用为主要考查点,重点考查学生分析问题、解决问题的能力.解析:画出可行域(如图中阴影部分),
由图可知,当直线经过点A(1,1)时,z最大,最大值为2×1+1=3.
答案:C
解析:作出可行域如图所示.
作直线l0:x-2y=0.
当把l0平移到l1位置时,此时过点A(1,-1),z的值最大,且zmax=1-2×(-1)=3.
答案:B
3.(2010·陕西高考)铁矿石A和B的含铁率a,冶炼每万吨
铁矿石的CO2的排放量b及每万吨铁矿石的价格c如下表:某冶炼厂至少要生产1.9(万吨)铁,若要求CO2的排放量不超过2(万吨),则购买铁矿石的最少费用为________(百万元).
答案:15
点击此图片进入“简单的线性规划习题复习” 简单的线性规划(习题复习)1. 在平面直角坐标系中,已知直线Ax+By+C=0和点P(x0,y0).若B>0,Ax0+By0+C>0,则点P在直线的①______;若B>0,Ax0+By0+C<0,则点P在直线的②_______.
2. 当B>0时,不等式Ax+By+C>0表示直线Ax+By+C=0③______的区域;当B<0时,不等式Ax+By+C>0表示直线Ax+By+C=0④_______的区域.上方下方上方下方3. 由关于x,y的二元一次不等式组成的不等式组称为⑤_________________;在线性约束条件下,求f(x,y)的最大值或最小值,则称关于x,y的解析式f(x,y)为⑥__________.
4. 满足线性约束条件的解(x,y)叫做⑦________;所有可行解组成的集合叫做⑧______;使目标函数达到最大值或最小值的可行解叫做⑨________.
5. 求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为⑩________问题.线性约束条件目标函数可行解可行域最优解线性规划1.点(-2,t)在直线2x-3y+6=0的上方,
则t的取值范围是( )
A. t>- B. t<-
C. t> D. t<
解:因为(-2,t)在直线2x-3y+6=0的上方,
则2×(-2)-3t+6<0,解得t > .C2.设变量x,y满足约束条件: 则目标函数z=2x+3y的最小值为( )
A. 6 B. 7 C. 8 D. 23
解:画出不等式组 表示
的可行域,如下图.B让目标函数表示直
线 在可行域
上平移,知在点B处目
标函数取到最小值,
解方程组
得B(2,1),
所以zmin=4+3=7,故选B.3.若不等式组 所表示的平面区域被直线 分为面积相等的两部分,则k的值是( )A解:不等式组表示的平面区域如图所示阴影部分△ABC.
由 得A(1,1).
又B(0,4),C(0, ),
所以
设y=kx+ 与3x+y=4的交点为D,
则由 知 所以
所以 所以 故选A.1. 画出下列不等式表示的平面区域.
(1)3x+2y+6>0;
(2)2x+y≤0;
(3)y2-x2≥0.题型1 画二元一次不等式表示的平面区域解:(1)先画直线3x+2y+6=0(画成虚线),取原点(0,0)代入3x+2y+6中得,3×0+2×0+6=6.
因为6>0,所以原点(0,0)在3x+2y+6>0表示的平面区域内,如图①所示.
(2)如图②所示. (3) y2-x2≥0
(y-x)(y+x)≥0
或
即 或
分别画出这两个不等式组表示的平面区
域,即所求区域,如图③.点评:画不等式表示的平面区域,按“线定界,点定域”,即先画不等式对应方程的曲线,然后任取曲线外的一点(常取原点),如果此点满足不等式,则这点所在区域就是;否则就为另一半区域.另外注意虚线与实线的画法. 在坐标平面上,求不等式组 所表示的平面区域的面积.
解:
或
如右图,△ABC的面积即为所求.
所以2. 已知x,y满足线性约束条件 分别求:
(1)u=4x-3y的最大值和最小值;
(2)z=x2+y2的最大值和最小值.
解:已知不等式组 题型2 求目标函数在约束条件下的最值在同一直角坐标系中作
直线x-2y+7=0,4x-3y-12=0和
x+2y-3=0,再根据不等式组
确定可行域为△ABC.
(1)由 解得点A的坐标为(9,8).
由 解得点C的坐标为(3,0).
由 解得点B的坐标为(-2, ).求u=4x-3y的最值,相当于求直线 中纵截距 的最值.显然,b最大时u最小,b最小时u最大.如图,当直线 与直线AC重合时,截距b=-4为最小,所以umax=-3b=12;
当直线 经过点B时,
截距 为最大,
所以(2)由图知,zmax=|OA|2=92+82=145.
因为原点O到直线BC的距离为
所以
点评:求目标函数的最值,其一般步骤是:先画出平面区域,找到相应的关键点,一般是边界线的交点,再结合目标函数的几何意义,通过图形计算得出答案.这是数形结合思想在解题中的具体应用. 已知 问(x+1)2+(y+1)2在何时取得最大值和最小值?最大值和最小值各是多少?
解:设z=(x+1)2+(y+1)2,
作出不等式组表示的平面区
域,如右图,各交点A(3,4),
B(1,3),C(2,1).z表示点M(x,y)与N(-1,-1)间距离的平方.过点N(-1,-1)作直线2x+y-5=0的垂线.
显然,垂足不在可行域内.
所以,当x=3,y=4时,z取得最大值;
当x=2,y=1时,z取得最小值.
所以zmax=(3+1)2+(4+1)2=41;
zmin=(2+1)2+(1+1)2=13.1. 判别二元一次不等式表示的区域有两种方法:①代点法;②讨论B>0时不等号的方向.
2. 可行域就是二元一次不等式组所表示的平面区域,可行域可以是封闭的多边形,也可以是一侧开放的无限大的平面区域.
3. 如果可行域是一个多边形,那么一般在其顶点处使目标函数取得最大值或最小值,最优解一般就是多边形的某个顶点.到底哪个顶点为最优解,有两种确定方法:一是将目标函数的直线平行移动,最先通过或最后通过的顶点便是;另一种方法可利用围成可行域的直线的斜率来判断.若围成可行域的直线l1,l2,…,ln的斜率满足k1<k2<…<kn,而且目标函数的直线的斜率为k,则当ki<k<ki+1时,直线li与li+1相交的顶点一般是最优解.
特别地,当表示线性目标函数的直线与可行域的某条边平行时(k=ki),其最优解可能有无数个.题型3 求线性规划中的参数值或取值范围1. 已知集合A={(x,y)|y≥ |x-2|},
B={(x,y)|y≤-|x|+b},且A∩B≠?.
(1)求b的取值范围;
(2)若(x,y)∈A∩B,且x+2y的最大值为8,
求b的值. 解:(1)分别画出不等式y≥ |x-2|和
y≤-|x|+b所表示的平面区域,如图.
因为A∩B≠?,
由图可知,b≥1,
所以b的取值范围是[1,+∞).
(2)平移直线x+2y=0,由图可知,
当这条直线经过点(0,b)时,
x+2y取得最大值.
所以0+2b=8,所以b=4.点评:在线性规划中,一般所取的最值与交点有关,即最优解一般与交点的坐标有关.而最优解的个数一般与线性约束条件中的直线的斜率有关,特别是求目标函数的含参斜率中的参数的取值范围问题,就与三条边界线有关.这种类型的问题体现了知识的逆向思维性和发散思维性.给出平面区域如右图所示,目标函数t=ax-y.
(1)若在区域上有无
穷多个点(x,y)可使目标
函数t取得最小值,求此时
a的值;
(2)若当且仅当 时,
目标函数t取得最小值,求实数a的取值范围.解:(1)由t=ax-y得y=ax-t.
要使t取得最小时的(x,y)有无穷多个,
则y=ax-t与BC或AC重合.
所以
或
(2)由kAC解:设生产甲、乙两种棉纱分别为x吨、y吨,总利润为z元. 题型4 线性规划在实际问题中的应用 依据题意, 且z=600x+900y.
作可行域,如图中阴影部分.
由 得
当直线l:600x+900y=z
经过点M(120,60)时,z最大,此时
z=600×120+900×60=126000(元).
答:生产甲种棉纱120吨、乙种棉纱60吨
时,才能使利润总额最大,最大利润为12.6万元.点评:线性规划在实际应用中较为广泛,利用线性规划解决应用问题可按下列步骤进行:①找到约束条件组,作出可行域;②设所求的目标函数f(x,y)=m;③将各顶点坐标代入目标函数,即可得m的最大值或最小值,或求直线f(x,y)=m在y轴上截距的最值,从而得到m的最值.如果使目标函数取得最值的点M(x0,y0)不是整数解,而x0、y0要求是整数,一般在确定与M点较近的两个点后,将此两点的坐标代入目标函数计算进行比较,从而确定其最优整数解. 本公司计划2012年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大?最大收益是多少万元?解:设该公司在甲电视台和乙电视台做广告的时间分别为x分钟和y分钟,总收益为z元.
由题意得
目标函数为z=3000x+2000y.
二元一次不等式组等价于作出不等式组所表示的平面区域,
即可行域,如图.
作直线l0:3000x+2000y=0,
即3x+2y=0.
平移直线l0,从图中可知,
当直线l过M点时,目标函数取
得最大值.
联立 解得所以点M的坐标为(100,200).所以
zmax=3000×100+2000×200=700000(元).
答:该公司在甲电视台做100分钟广告,在乙电视台做200分钟广告,公司的收益最大,最大收益是70万元.3. 将甲、乙两种长短不同的钢管截成A、B、C三种规格,每根钢管可同时截得三种规格的短钢管的根数如下表所示:
现在需要A、B、C三种规格的钢管分别为13、16、18根,问应分别截甲、乙两种钢管各多少根,才能使材料利用率最高? 题型5 线性规划中的整点问题解:设截甲、乙两种钢管分别为x根、y根,z=x+y,依题意得
作可行域,由图知,当直线x+y=z过点A时,z为最小.由 得 所以点
因为x,y∈N*,在可行域内与点A邻近的整点有(4,4),(4,5).显然(4,4)是最优解,且zmin=8.
故分别截取甲、乙两种钢管各4根,才能使材料利用率最高. 某校高二(1)班举行元旦文艺晚会,布置会场要制作“中国结”,班长购买了甲、乙两种颜色不同的彩绳,把它们截成A、B、C三种规格.甲种彩绳每根8元,乙种彩绳每根6元,已知每根彩绳可同时截得三种规格彩绳的根数如下表所示:今需要A、B、C三种规格的彩绳各15、18、27根,问各截这两种彩绳多少根,可得所需三种规格彩绳且花费最少?
解:设需购买甲种彩绳x根、乙种彩绳y根,共花费z元,
则
且z=8x+6y.
作可行域,由图可知,
直线l经过可行域内的点A时,z最小.由 得 所以点A(3.6,7.8).
因为x,y∈N,在可行域内与点A邻近的整
点有(3,9),(4,8).
显然(3,9)是最优解,且zmin=78.
答:班长应购买3根甲种彩绳、9根乙种
彩绳,可使花费最少.1. 解线性规划应用题的一般步骤:①设出决策变量,找出约束条件和线性目标函数;②利用图象在约束条件下找出决策变量使目标函数达到最大或最小.
2. 若实际问题要求的最优解是整数解,而我们利用图解法得到的解为非整数解(近似解),应作适当的调整.其方法应以与线性目标函数的直线的距离为依据,在直线附近寻找与此直线距离最近的整点,不要在用图解法所得到的近似解附近寻找.如果可行域中的整点数目很少,逐个检验亦可.
2.了解二元一次不等式的几何意义,能用平面区域
表示二元一次不等式组.
3.会从实际情境中抽象出一些简单的二元线性规划
问题,并能加以解决.
?3.3 二元一次不等式组与简单的线性规划问题[理 要 点]
一、二元一次不等式表示平面区域
1.二元一次不等式Ax+By+C>0在平面直角坐标系中表示
直线Ax+By+C=0某一侧的所有点组成的平面区域(半平面), 边界直线.
不等式Ax+By+C≥0所表示的平面区域(半平面) 边界直线.
不含包含2.对于直线Ax+By+C=0同一侧的所有点(x,y),使得Ax+By+C的值符号相同,也就是位于同一半平面内的点,其坐标适合 ;而位于另一个半平面内的点,其坐标适合Ax+By+C>0Ax+By+C<03.可在直线Ax+By+C=0的某一侧任取一点,一般取特殊点(x0,y0),从Ax0+By0+C的 来判断Ax+By+C>0(或Ax+By+C<0)所表示的区域.
正负4.由几个不等式组成的不等式组所表示的平面区域,是
各个不等式所表示的平面区域的 .
公共部分二、线性规划中的基本概念不等式(组)
一次解析式一次(x,y)最大值最小值最大值最小值集合?[究 疑 点]
1.可行解与最优解有何关系?最优解是否唯一?
提示:最优解必定是可行解,但可行解不一定是最优解.最优解不一定唯一,有时唯一,有时有多个.
2.点P1(x1,y1)和P2(x2,y2)位于直线Ax+By+C=0的两侧的首要条件是什么?
提示:(Ax1+By1+C)(Ax2+By2+C)<0.
[题组自测]
1.如图所示的平面区域(阴影部分)满
足不等式 ( )
A.x+y-1<0
B.x+y-1>0
C.x-y-1<0
D.x-y-1>0答案: B解:(1)先画出直线2x+y-10=0(画成虚线).
取原点(0,0),代入2x+y-10,∵2×0+0-10<0,
∴原点在2x+y-10<0表示的平面区域内,
不等式2x+y-10<0表示的区域如图(1)所示.
(2)不等式x-y+5≥0表示直线x-y+5=0上及右下方的点的集合,x+y+1≥0表示直线x+y+1=0上及右上方的点的集合,x≤3表示直线x=3上及左方的点的集合,所以不等式组表示的平面区域如图(2)所示.
(2)如图,△ABC中,A(0,1),B(-2,2),C(2,6),写出△ABC区域所表示的二元一次不等式组.
答案:(1)A
[归纳领悟]
二元一次不等式(组)表示平面区域的判定方法:
直线定界、特殊点定域.注意不等式是否可取等号,不可取等号时直线画成虚线,可取等号时直线画成实线.若直线不过原点,特殊点常选取原点.答案:A
答案:5
[归纳领悟]
求目标函数的最值的一般步骤是:一画二移三求,其关键是准确作出可行域,准确理解z的几何意义,对于目标函数z=ax+by而言,当b>0时,在可行域内越向上平移直线ax+by=0,z的值越大;越向下平移直线ax+by=0,z的值越小.当b<0时,情况正好相反.[题组自测]
1.一项装修工程需要木工和瓦工共同完成,请木工需付
工资每人50元,请瓦工需付工资每人40元,现有工人工资预算2 000元,设木工x人,瓦工y人,请工人的约束条件是______________.
2.(2010·四川高考)某加工厂用某原料由甲车间加工出A产
品,由乙车间加工出B产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克A产品,每千克A产品获利40元.乙车间加工一箱原料需耗费工时6小时可加工出4千克B产品,每千克B产品获利50元.甲、乙两车间每天共能完成至多70箱原料的加工,每天甲、乙两车间耗费工时总和不得超过480小时,甲、乙两车间每天总获利最大的生产计划为 ( )A.甲车间加工原料10箱,乙车间加工原料60箱
B.甲车间加工原料15箱,乙车间加工原料55箱
C.甲车间加工原料18箱,乙车间加工原料50箱
D.甲车间加工原料40箱,乙车间加工原料30箱
答案:B
3.某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种
玩具共100个,生产一个卫兵需5分钟,生产一个骑兵需7分钟,生产一个伞兵需4分钟,已知总生产时间不超过10小时.若生产一个卫兵可获利润5元,生产一个骑兵可获利润6元,生产一个伞兵可获利润3元.
(1)用每天生产的卫兵个数x与骑兵个数y表示每天的利润w(元);
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
解:(1)依题意每天生产的伞兵个数为100-x-y,所以利润w=5x+6y+3(100-x-y)=2x+3y+300.[归纳领悟]
线性规划实际应用问题的解决常见的错误点有:
(1)不能准确地理解题中条件的含义,如“不超过”、“至
少”等线性约束条件出现失误.
(2)最优解的找法由于作图不规范而不准确.
(3)最大解为“整点时”不会寻找“最优整点解”.处理此类
问题时.一是要规范作图,尤其是边界实虚要分清,二是寻找最优整点解时可记住“整点在整线上”(整线:形如x=k或y=k,k∈Z).
一、把脉考情
从近两年的高考试题来看,二元一次不等式(组)表示的平面区域(的面积)、求目标函数的最值、线性规划的应用问题等是高考的热点,题型既有选择题,也有填空题,难度为中低档题;主要考查平面区域的画法、目标函数最值的求法,以及在取得最值时参数的取值范围.同时注重考查等价转化、数形结合思想.
预测2012年高考仍将以目标函数的最值、线性规划的综合运用为主要考查点,重点考查学生分析问题、解决问题的能力.解析:画出可行域(如图中阴影部分),
由图可知,当直线经过点A(1,1)时,z最大,最大值为2×1+1=3.
答案:C
解析:作出可行域如图所示.
作直线l0:x-2y=0.
当把l0平移到l1位置时,此时过点A(1,-1),z的值最大,且zmax=1-2×(-1)=3.
答案:B
3.(2010·陕西高考)铁矿石A和B的含铁率a,冶炼每万吨
铁矿石的CO2的排放量b及每万吨铁矿石的价格c如下表:某冶炼厂至少要生产1.9(万吨)铁,若要求CO2的排放量不超过2(万吨),则购买铁矿石的最少费用为________(百万元).
答案:15
点击此图片进入“简单的线性规划习题复习” 简单的线性规划(习题复习)1. 在平面直角坐标系中,已知直线Ax+By+C=0和点P(x0,y0).若B>0,Ax0+By0+C>0,则点P在直线的①______;若B>0,Ax0+By0+C<0,则点P在直线的②_______.
2. 当B>0时,不等式Ax+By+C>0表示直线Ax+By+C=0③______的区域;当B<0时,不等式Ax+By+C>0表示直线Ax+By+C=0④_______的区域.上方下方上方下方3. 由关于x,y的二元一次不等式组成的不等式组称为⑤_________________;在线性约束条件下,求f(x,y)的最大值或最小值,则称关于x,y的解析式f(x,y)为⑥__________.
4. 满足线性约束条件的解(x,y)叫做⑦________;所有可行解组成的集合叫做⑧______;使目标函数达到最大值或最小值的可行解叫做⑨________.
5. 求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为⑩________问题.线性约束条件目标函数可行解可行域最优解线性规划1.点(-2,t)在直线2x-3y+6=0的上方,
则t的取值范围是( )
A. t>- B. t<-
C. t> D. t<
解:因为(-2,t)在直线2x-3y+6=0的上方,
则2×(-2)-3t+6<0,解得t > .C2.设变量x,y满足约束条件: 则目标函数z=2x+3y的最小值为( )
A. 6 B. 7 C. 8 D. 23
解:画出不等式组 表示
的可行域,如下图.B让目标函数表示直
线 在可行域
上平移,知在点B处目
标函数取到最小值,
解方程组
得B(2,1),
所以zmin=4+3=7,故选B.3.若不等式组 所表示的平面区域被直线 分为面积相等的两部分,则k的值是( )A解:不等式组表示的平面区域如图所示阴影部分△ABC.
由 得A(1,1).
又B(0,4),C(0, ),
所以
设y=kx+ 与3x+y=4的交点为D,
则由 知 所以
所以 所以 故选A.1. 画出下列不等式表示的平面区域.
(1)3x+2y+6>0;
(2)2x+y≤0;
(3)y2-x2≥0.题型1 画二元一次不等式表示的平面区域解:(1)先画直线3x+2y+6=0(画成虚线),取原点(0,0)代入3x+2y+6中得,3×0+2×0+6=6.
因为6>0,所以原点(0,0)在3x+2y+6>0表示的平面区域内,如图①所示.
(2)如图②所示. (3) y2-x2≥0
(y-x)(y+x)≥0
或
即 或
分别画出这两个不等式组表示的平面区
域,即所求区域,如图③.点评:画不等式表示的平面区域,按“线定界,点定域”,即先画不等式对应方程的曲线,然后任取曲线外的一点(常取原点),如果此点满足不等式,则这点所在区域就是;否则就为另一半区域.另外注意虚线与实线的画法. 在坐标平面上,求不等式组 所表示的平面区域的面积.
解:
或
如右图,△ABC的面积即为所求.
所以2. 已知x,y满足线性约束条件 分别求:
(1)u=4x-3y的最大值和最小值;
(2)z=x2+y2的最大值和最小值.
解:已知不等式组 题型2 求目标函数在约束条件下的最值在同一直角坐标系中作
直线x-2y+7=0,4x-3y-12=0和
x+2y-3=0,再根据不等式组
确定可行域为△ABC.
(1)由 解得点A的坐标为(9,8).
由 解得点C的坐标为(3,0).
由 解得点B的坐标为(-2, ).求u=4x-3y的最值,相当于求直线 中纵截距 的最值.显然,b最大时u最小,b最小时u最大.如图,当直线 与直线AC重合时,截距b=-4为最小,所以umax=-3b=12;
当直线 经过点B时,
截距 为最大,
所以(2)由图知,zmax=|OA|2=92+82=145.
因为原点O到直线BC的距离为
所以
点评:求目标函数的最值,其一般步骤是:先画出平面区域,找到相应的关键点,一般是边界线的交点,再结合目标函数的几何意义,通过图形计算得出答案.这是数形结合思想在解题中的具体应用. 已知 问(x+1)2+(y+1)2在何时取得最大值和最小值?最大值和最小值各是多少?
解:设z=(x+1)2+(y+1)2,
作出不等式组表示的平面区
域,如右图,各交点A(3,4),
B(1,3),C(2,1).z表示点M(x,y)与N(-1,-1)间距离的平方.过点N(-1,-1)作直线2x+y-5=0的垂线.
显然,垂足不在可行域内.
所以,当x=3,y=4时,z取得最大值;
当x=2,y=1时,z取得最小值.
所以zmax=(3+1)2+(4+1)2=41;
zmin=(2+1)2+(1+1)2=13.1. 判别二元一次不等式表示的区域有两种方法:①代点法;②讨论B>0时不等号的方向.
2. 可行域就是二元一次不等式组所表示的平面区域,可行域可以是封闭的多边形,也可以是一侧开放的无限大的平面区域.
3. 如果可行域是一个多边形,那么一般在其顶点处使目标函数取得最大值或最小值,最优解一般就是多边形的某个顶点.到底哪个顶点为最优解,有两种确定方法:一是将目标函数的直线平行移动,最先通过或最后通过的顶点便是;另一种方法可利用围成可行域的直线的斜率来判断.若围成可行域的直线l1,l2,…,ln的斜率满足k1<k2<…<kn,而且目标函数的直线的斜率为k,则当ki<k<ki+1时,直线li与li+1相交的顶点一般是最优解.
特别地,当表示线性目标函数的直线与可行域的某条边平行时(k=ki),其最优解可能有无数个.题型3 求线性规划中的参数值或取值范围1. 已知集合A={(x,y)|y≥ |x-2|},
B={(x,y)|y≤-|x|+b},且A∩B≠?.
(1)求b的取值范围;
(2)若(x,y)∈A∩B,且x+2y的最大值为8,
求b的值. 解:(1)分别画出不等式y≥ |x-2|和
y≤-|x|+b所表示的平面区域,如图.
因为A∩B≠?,
由图可知,b≥1,
所以b的取值范围是[1,+∞).
(2)平移直线x+2y=0,由图可知,
当这条直线经过点(0,b)时,
x+2y取得最大值.
所以0+2b=8,所以b=4.点评:在线性规划中,一般所取的最值与交点有关,即最优解一般与交点的坐标有关.而最优解的个数一般与线性约束条件中的直线的斜率有关,特别是求目标函数的含参斜率中的参数的取值范围问题,就与三条边界线有关.这种类型的问题体现了知识的逆向思维性和发散思维性.给出平面区域如右图所示,目标函数t=ax-y.
(1)若在区域上有无
穷多个点(x,y)可使目标
函数t取得最小值,求此时
a的值;
(2)若当且仅当 时,
目标函数t取得最小值,求实数a的取值范围.解:(1)由t=ax-y得y=ax-t.
要使t取得最小时的(x,y)有无穷多个,
则y=ax-t与BC或AC重合.
所以
或
(2)由kAC
作可行域,如图中阴影部分.
由 得
当直线l:600x+900y=z
经过点M(120,60)时,z最大,此时
z=600×120+900×60=126000(元).
答:生产甲种棉纱120吨、乙种棉纱60吨
时,才能使利润总额最大,最大利润为12.6万元.点评:线性规划在实际应用中较为广泛,利用线性规划解决应用问题可按下列步骤进行:①找到约束条件组,作出可行域;②设所求的目标函数f(x,y)=m;③将各顶点坐标代入目标函数,即可得m的最大值或最小值,或求直线f(x,y)=m在y轴上截距的最值,从而得到m的最值.如果使目标函数取得最值的点M(x0,y0)不是整数解,而x0、y0要求是整数,一般在确定与M点较近的两个点后,将此两点的坐标代入目标函数计算进行比较,从而确定其最优整数解. 本公司计划2012年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大?最大收益是多少万元?解:设该公司在甲电视台和乙电视台做广告的时间分别为x分钟和y分钟,总收益为z元.
由题意得
目标函数为z=3000x+2000y.
二元一次不等式组等价于作出不等式组所表示的平面区域,
即可行域,如图.
作直线l0:3000x+2000y=0,
即3x+2y=0.
平移直线l0,从图中可知,
当直线l过M点时,目标函数取
得最大值.
联立 解得所以点M的坐标为(100,200).所以
zmax=3000×100+2000×200=700000(元).
答:该公司在甲电视台做100分钟广告,在乙电视台做200分钟广告,公司的收益最大,最大收益是70万元.3. 将甲、乙两种长短不同的钢管截成A、B、C三种规格,每根钢管可同时截得三种规格的短钢管的根数如下表所示:
现在需要A、B、C三种规格的钢管分别为13、16、18根,问应分别截甲、乙两种钢管各多少根,才能使材料利用率最高? 题型5 线性规划中的整点问题解:设截甲、乙两种钢管分别为x根、y根,z=x+y,依题意得
作可行域,由图知,当直线x+y=z过点A时,z为最小.由 得 所以点
因为x,y∈N*,在可行域内与点A邻近的整点有(4,4),(4,5).显然(4,4)是最优解,且zmin=8.
故分别截取甲、乙两种钢管各4根,才能使材料利用率最高. 某校高二(1)班举行元旦文艺晚会,布置会场要制作“中国结”,班长购买了甲、乙两种颜色不同的彩绳,把它们截成A、B、C三种规格.甲种彩绳每根8元,乙种彩绳每根6元,已知每根彩绳可同时截得三种规格彩绳的根数如下表所示:今需要A、B、C三种规格的彩绳各15、18、27根,问各截这两种彩绳多少根,可得所需三种规格彩绳且花费最少?
解:设需购买甲种彩绳x根、乙种彩绳y根,共花费z元,
则
且z=8x+6y.
作可行域,由图可知,
直线l经过可行域内的点A时,z最小.由 得 所以点A(3.6,7.8).
因为x,y∈N,在可行域内与点A邻近的整
点有(3,9),(4,8).
显然(3,9)是最优解,且zmin=78.
答:班长应购买3根甲种彩绳、9根乙种
彩绳,可使花费最少.1. 解线性规划应用题的一般步骤:①设出决策变量,找出约束条件和线性目标函数;②利用图象在约束条件下找出决策变量使目标函数达到最大或最小.
2. 若实际问题要求的最优解是整数解,而我们利用图解法得到的解为非整数解(近似解),应作适当的调整.其方法应以与线性目标函数的直线的距离为依据,在直线附近寻找与此直线距离最近的整点,不要在用图解法所得到的近似解附近寻找.如果可行域中的整点数目很少,逐个检验亦可.
