数学高中苏教版必修五2.1《数列》课件3
文档属性
| 名称 | 数学高中苏教版必修五2.1《数列》课件3 |  | |
| 格式 | zip | ||
| 文件大小 | 277.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-05 11:56:29 | ||
图片预览








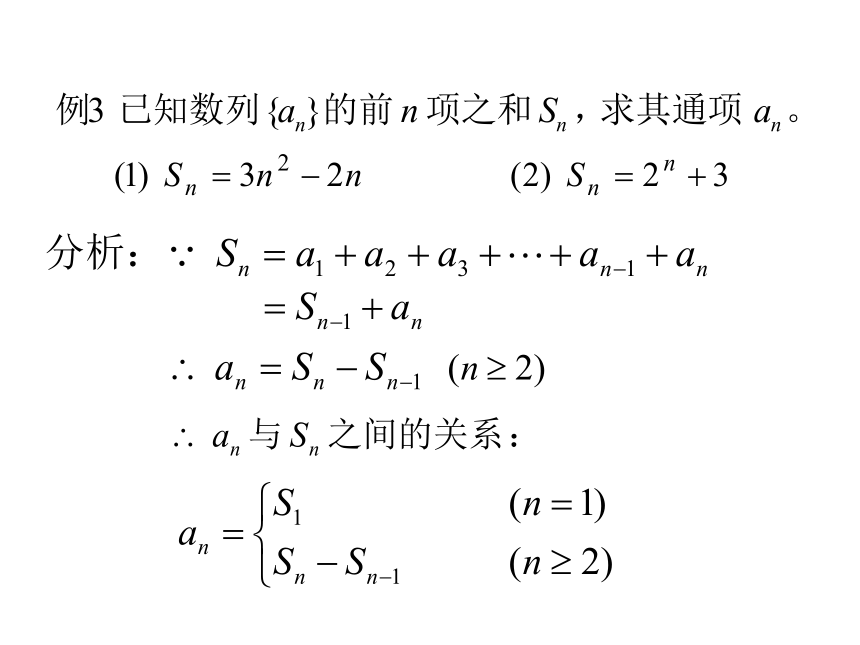
文档简介
课件22张PPT。2.1数列的概念和简单表示法(二)1. 数列定义:按一定的次序排列的一列数叫做数列.数列中的每一个数都叫做这个数列的项.2. 数列表示数列的一般形式是简记作:3. 通项公式 函数观点看:数列可以看作是一个定义域为正整数集N*(或其有限子集)的函数当自变量从小到大依次取值时对应的一列函数值,而数列的通项公式也就是相应函数的解析式.y=f(x)ann函数值自变量 如果数列{ an }的第n项an与n之间的关
系可以用一个公式来表示,则称此公式为
数列的通项公式。(1)按项数有限还是无限分为
有穷数列、无穷数列。4. 数列的分类 (2)按项与项之间的大小关系分为:
递增数列 (an+1 >an )、递减数列 (an+1摆动数列、常数列 . (3)按任何一项绝对值是否都小于某一正数分为:有界数列、无界数列。5. 递推公式 如果已知数列{an}的第1项 (或前几项),且任一项 an 与它的前一项 an-1 (或前几项) 间的关系可用一个公式表达,这个公式叫数列的递推公式。
说明:递推公式也是给出数列的一种方法.例1:已知数列 的首项为1,以后各项由公式 给出,写出该数列前5项解:例2:已知 数列 1,1,2,3,5,8,13,21,34,··· ,
请写出它的一个递推公式 .解:观察数列的前 n 项,有:a1=a2=1a3= 2 =1+1= a1+a2a4= 3 =1+2= a2+a3a5= 5 =2+3= a3+a4···∴ an= an-2+an-1 (n≥3) 为所求递推公式.4例52 .根据下面各数列的前几项的值,写出数列的一个通项公式: P122 练 习:写出下列数列 {an}的前5项:解:6例7 已知数列 是递减数列,
求实数m的取值范围.解:∵ 数列是递减数列,解得课后作业2.教辅课时作业第13页 2.1(二)4.预习教材第36页 ~39页内容3.教辅第23页 ~第25页内容1.教材材第34页 习题2.1 B组 1~3
系可以用一个公式来表示,则称此公式为
数列的通项公式。(1)按项数有限还是无限分为
有穷数列、无穷数列。4. 数列的分类 (2)按项与项之间的大小关系分为:
递增数列 (an+1 >an )、递减数列 (an+1
请写出它的一个递推公式 .解:观察数列的前 n 项,有:a1=a2=1a3= 2 =1+1= a1+a2a4= 3 =1+2= a2+a3a5= 5 =2+3= a3+a4···∴ an= an-2+an-1 (n≥3) 为所求递推公式.4例52 .根据下面各数列的前几项的值,写出数列的一个通项公式: P122 练 习:写出下列数列 {an}的前5项:解:6例7 已知数列 是递减数列,
求实数m的取值范围.解:∵ 数列是递减数列,解得课后作业2.教辅课时作业第13页 2.1(二)4.预习教材第36页 ~39页内容3.教辅第23页 ~第25页内容1.教材材第34页 习题2.1 B组 1~3
