数学高中苏教版必修五第二章《数列》复习课件
文档属性
| 名称 | 数学高中苏教版必修五第二章《数列》复习课件 |  | |
| 格式 | zip | ||
| 文件大小 | 79.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-05 13:04:35 | ||
图片预览

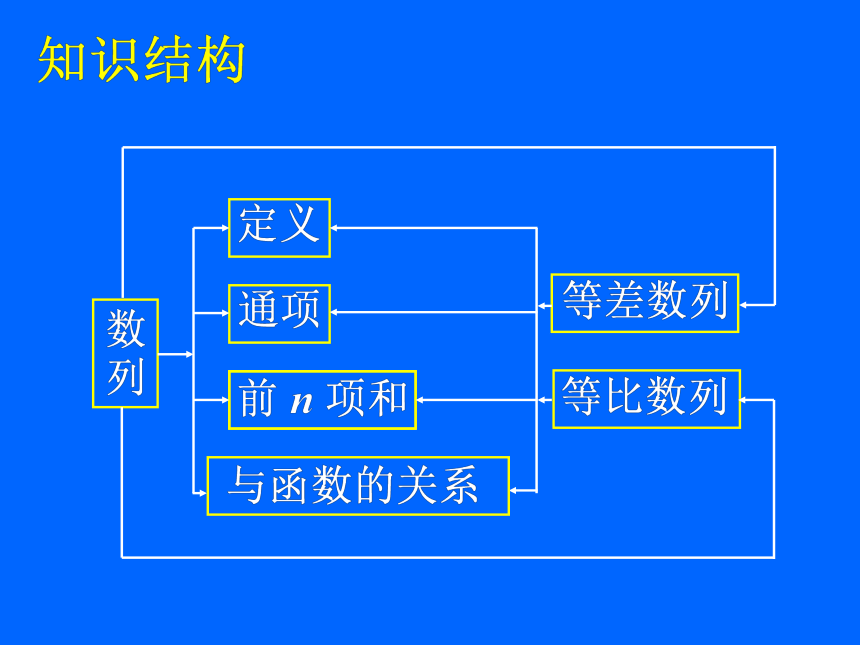







文档简介
课件21张PPT。第二章数列复习知识归纳等差数列定 义通 项前n项和主要性质1.等差数列这单元学习了哪些内容?一、等差数列2. 等差数列的定义、用途及使用时需
注意的问题:n≥2,an -an-1=d (常数)3. 等差数列的通项公式如何?结构有
什么特点?an=a1+(n-1) dan=An+B(d=A∈R)一、等差数列4. 等差数列图象有什么特点?
单调性如何确定?nnanand>0d<0一、等差数列5. 用什么方法推导等差数列前n项和公式
的?公式内容? 使用时需注意的问题? 前n
项和公式结构有什么特点?Sn=An2+Bn (A∈R) 注意: d=2A !一、等差数列6. 你知道等差数列的哪些性质?等差数列{an}中,(m、 n、p、q∈N+):
①an=am+(n-m)d ;
②若 m+n=p+q,则am+an=ap+aq ;
③由项数成等差数列的项组成的数列仍
是等差数列;
④ 每n项和Sn , S2n-Sn , S3n-S2n …
组成的数列仍是等差数列.一、等差数列1. 等比数列的定义2. 等比数列的通项公式3. 等比中项二、等比数列4. 等比数列的判定方法(1) an=an-1·q (n≥2),q是不为零的常数,
an-1≠0 ? {an}是等比数列.
(2) an2=an-1·an+1(n≥2, an-1, an, an+1≠0)
? {an}是等比数列.
(3) an=c·qn (c,q均是不为零的常数)
? {an}是等比数列.二、等比数列5. 等比数列的性质 (1)当q>1,a1>0或0<q<1,a1<0时,
{an}是递增数列;
当q>1,a1<0或0<q<1,a1>0时,
{an}是递减数列;
当q=1时,{an}是常数列;
当q<0时,{an}是摆动数列.二、等比数列5. 等比数列的性质 (2)an=am·qn-m(m、n∈N*).(1)当q>1,a1>0或0<q<1,a1<0时,
{an}是递增数列;
当q>1,a1<0或0<q<1,a1>0时,
{an}是递减数列;
当q=1时,{an}是常数列;
当q<0时,{an}是摆动数列.二、等比数列6. 等比数列的前n项和公式 二、等比数列7. 等比数列前n项和的一般形式二、等比数列8. 等比数列的前n项和的性质二、等比数列(1)在等比数列中,若项数为2n(n∈N*),
则(2)Sn,S2n-Sn,S3n-S2n成等比数列.8. 等比数列的前n项和的性质(1)在等比数列中,若项数为2n(n∈N*),
则二、等比数列1. 已知: x>0,y>0, x,a,b,y成等差数
列,x,c,d,y成等比数列,则的最小值是 ( ) A. 0 B. 1 C. 2 D. 4练习2. 数列{an}的前n项和记作Sn,满足
Sn=2an+3n-12(n∈N*).
(1)证明数列{an-3}为等比数列;
并求出数列{an}的通项公式.
(2)记bn=nan ,数列{bn}的前n项
和为Tn ,求Tn.练习3.已知实数列{an}是等比数列,其中
a7=1,且a4,a5+1,a6成等差数列.
(1)求数列{an}的通项公式;
(2)数列{an}的前n项和记为Sn,
证明:Sn<128(n=1,2,3,…).练习4.设数列{an}的前n项和为Sn=2n2,{bn}
为等比数列,且a1=b1,b2(a2-a1)=b1,
(1)求数列{an}和{bn}的通项公式;
(2)设 ,求数列{cn}的前n项和Tn .练习
注意的问题:n≥2,an -an-1=d (常数)3. 等差数列的通项公式如何?结构有
什么特点?an=a1+(n-1) dan=An+B(d=A∈R)一、等差数列4. 等差数列图象有什么特点?
单调性如何确定?nnanand>0d<0一、等差数列5. 用什么方法推导等差数列前n项和公式
的?公式内容? 使用时需注意的问题? 前n
项和公式结构有什么特点?Sn=An2+Bn (A∈R) 注意: d=2A !一、等差数列6. 你知道等差数列的哪些性质?等差数列{an}中,(m、 n、p、q∈N+):
①an=am+(n-m)d ;
②若 m+n=p+q,则am+an=ap+aq ;
③由项数成等差数列的项组成的数列仍
是等差数列;
④ 每n项和Sn , S2n-Sn , S3n-S2n …
组成的数列仍是等差数列.一、等差数列1. 等比数列的定义2. 等比数列的通项公式3. 等比中项二、等比数列4. 等比数列的判定方法(1) an=an-1·q (n≥2),q是不为零的常数,
an-1≠0 ? {an}是等比数列.
(2) an2=an-1·an+1(n≥2, an-1, an, an+1≠0)
? {an}是等比数列.
(3) an=c·qn (c,q均是不为零的常数)
? {an}是等比数列.二、等比数列5. 等比数列的性质 (1)当q>1,a1>0或0<q<1,a1<0时,
{an}是递增数列;
当q>1,a1<0或0<q<1,a1>0时,
{an}是递减数列;
当q=1时,{an}是常数列;
当q<0时,{an}是摆动数列.二、等比数列5. 等比数列的性质 (2)an=am·qn-m(m、n∈N*).(1)当q>1,a1>0或0<q<1,a1<0时,
{an}是递增数列;
当q>1,a1<0或0<q<1,a1>0时,
{an}是递减数列;
当q=1时,{an}是常数列;
当q<0时,{an}是摆动数列.二、等比数列6. 等比数列的前n项和公式 二、等比数列7. 等比数列前n项和的一般形式二、等比数列8. 等比数列的前n项和的性质二、等比数列(1)在等比数列中,若项数为2n(n∈N*),
则(2)Sn,S2n-Sn,S3n-S2n成等比数列.8. 等比数列的前n项和的性质(1)在等比数列中,若项数为2n(n∈N*),
则二、等比数列1. 已知: x>0,y>0, x,a,b,y成等差数
列,x,c,d,y成等比数列,则的最小值是 ( ) A. 0 B. 1 C. 2 D. 4练习2. 数列{an}的前n项和记作Sn,满足
Sn=2an+3n-12(n∈N*).
(1)证明数列{an-3}为等比数列;
并求出数列{an}的通项公式.
(2)记bn=nan ,数列{bn}的前n项
和为Tn ,求Tn.练习3.已知实数列{an}是等比数列,其中
a7=1,且a4,a5+1,a6成等差数列.
(1)求数列{an}的通项公式;
(2)数列{an}的前n项和记为Sn,
证明:Sn<128(n=1,2,3,…).练习4.设数列{an}的前n项和为Sn=2n2,{bn}
为等比数列,且a1=b1,b2(a2-a1)=b1,
(1)求数列{an}和{bn}的通项公式;
(2)设 ,求数列{cn}的前n项和Tn .练习
