数学高中苏教版必修四1.1《任意角、弧度》课件
文档属性
| 名称 | 数学高中苏教版必修四1.1《任意角、弧度》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 324.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-05 13:17:28 | ||
图片预览







文档简介
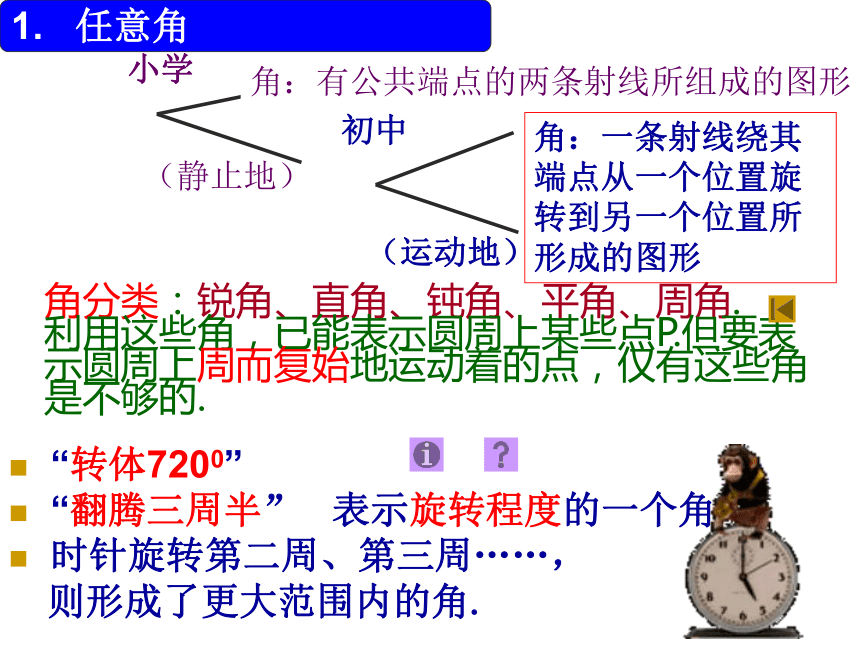
课件28张PPT。1. 任意角角分类:锐角、直角、钝角、平角、周角.
利用这些角,已能表示圆周上某些点P.但要表示圆周上周而复始地运动着的点,仅有这些角是不够的.“转体7200”
“翻腾三周半” 表示旋转程度的一个角
时针旋转第二周、第三周……,
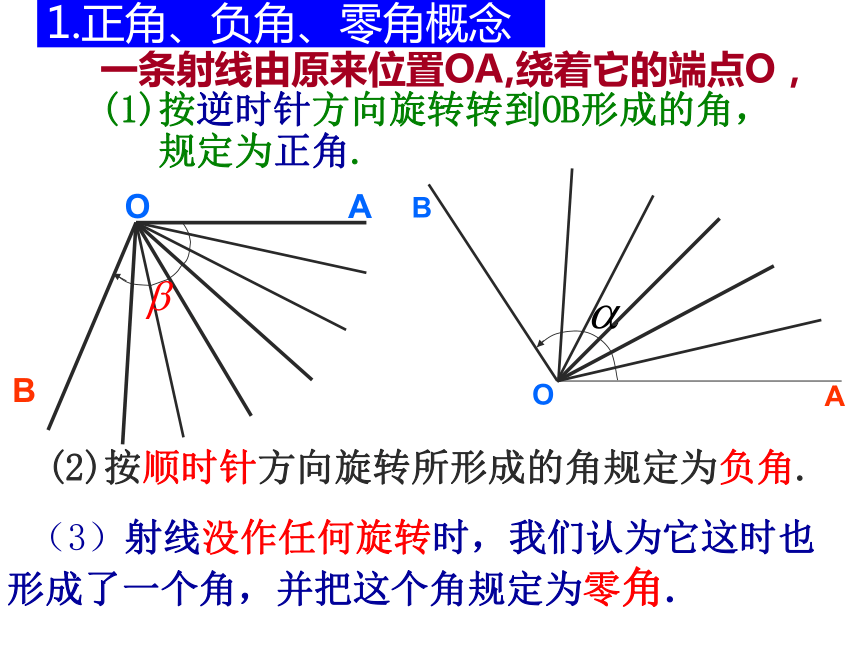
则形成了更大范围内的角.角:有公共端点的两条射线所组成的图形角:一条射线绕其端点从一个位置旋转到另一个位置所形成的图形1.正角、负角、零角概念B一条射线由原来位置OA,绕着它的端点O,(1)按逆时针方向旋转转到OB形成的角, 规定为正角.(2)按顺时针方向旋转所形成的角规定为负角.OAB (3)射线没作任何旋转时,我们认为它这时也形成了一个角,并把这个角规定为零角.为了便于研究,今后我们常以角的顶点为坐标原点,角的始边为x轴正半轴,建立平面直角坐标系.第几象限角:
角的终边(除端点外)落在第几象限,就称这个角是第几象限角.
轴线角:
如果角的终边落在坐标轴上,就说该角不属于任何象限,习惯上称其为轴线角.象限角的表示练习:分别作出下列各角,并指出它们分别是第几象限角?其中哪些角的终边相同?-300o、 -150o、 -60o、 60o、 210o、 300o、 420o二、例题讲解例1:在0o到360o的范围内,找出与下列各角终边相同的角,并分别判断他们是第几象限角:
(1) 650o (2) -150o (3) -990o15 练习:P7,1、2、3 、4 小结4.求与α终边相同的周内角(0o~360o),用草除法,商为k值,余数即为所求, 注意负角商的绝对值要比实际商大1 。 一、角度制 1、用“度”作单位来度量角的单位制称作 “角度制”,规定:圆周1/360的圆心角称作1°角。 2、角度制的单位有:度、分、秒。 1、定义:我们把等于半径长的圆弧所对的圆心角叫做1弧度的角。演示 问题:若弧是一个半圆,则其圆心角的弧度数是多少?若弧是一个整圆呢?二、弧度制定义 2.单位:弧度(或rad) 4、为什么可以用弧长与其半径的比值来度量角的大小呢?即这个比值是否与所取的圆的半径大小无关呢? 二、弧度制定义 角度制与弧度制的互换:(1)把角度换成弧度(2)把弧度换成角度解:∵四、例题讲解 解:四、例题讲解 正角的弧度数是一个正数;
负角的弧度数是一个负数;
零角的弧度数是0.一些特殊角的弧度数 ①、弧度制是以“弧度”为单位度量角的制度,角度制是以“度”为单位度量角的制度; ②、1弧度是等于半径长的圆弧所对的圆心角(或该弧)的大小;③、不论是以“弧度”还是以“度”为单位的角的大小都是一个与半径大小无关的定值.角度制与弧度制的比较例3:计算四、例题讲解 四、例题讲解 弧长公式和扇形面积公式1、弧长公式:2、扇形面积公式:练习:1.在半径不等的两个圆内,1弧度的圆心角( )
A.所对弧长相等 B.所对的弦长相等
C.所对弧长等于各自半径 D.所对的弧长为例4:已知扇形的周长为8cm,圆心角为2弧度,求该扇形的面积.C解:设扇形的半径为r,弧长为l,则有小结我们把等于半径长的圆弧所对的圆心角叫做1弧度的角.求角的大小:
(2)方向:正角的弧度数是一个正数;
负角的弧度数是一个负数;
零角的弧度数是0.练习:求图中公路弯道处弧 的长 。
(精确到 ,图中长度单位: )解:练习2、若三角形的三个内角之比是2:3:4,求其三个内角的弧度数.1.若三角形的三个内角之比是2:3:4,求其三个内角的弧度数.
“翻腾三周半” 表示旋转程度的一个角
时针旋转第二周、第三周……,
则形成了更大范围内的角.角:有公共端点的两条射线所组成的图形角:一条射线绕其端点从一个位置旋转到另一个位置所形成的图形1.正角、负角、零角概念B一条射线由原来位置OA,绕着它的端点O,(1)按逆时针方向旋转转到OB形成的角, 规定为正角.(2)按顺时针方向旋转所形成的角规定为负角.OAB (3)射线没作任何旋转时,我们认为它这时也形成了一个角,并把这个角规定为零角.为了便于研究,今后我们常以角的顶点为坐标原点,角的始边为x轴正半轴,建立平面直角坐标系.第几象限角:
角的终边(除端点外)落在第几象限,就称这个角是第几象限角.
轴线角:
如果角的终边落在坐标轴上,就说该角不属于任何象限,习惯上称其为轴线角.象限角的表示练习:分别作出下列各角,并指出它们分别是第几象限角?其中哪些角的终边相同?-300o、 -150o、 -60o、 60o、 210o、 300o、 420o二、例题讲解例1:在0o到360o的范围内,找出与下列各角终边相同的角,并分别判断他们是第几象限角:
(1) 650o (2) -150o (3) -990o15 练习:P7,1、2、3 、4 小结4.求与α终边相同的周内角(0o~360o),用草除法,商为k值,余数即为所求, 注意负角商的绝对值要比实际商大1 。 一、角度制 1、用“度”作单位来度量角的单位制称作 “角度制”,规定:圆周1/360的圆心角称作1°角。 2、角度制的单位有:度、分、秒。 1、定义:我们把等于半径长的圆弧所对的圆心角叫做1弧度的角。演示 问题:若弧是一个半圆,则其圆心角的弧度数是多少?若弧是一个整圆呢?二、弧度制定义 2.单位:弧度(或rad) 4、为什么可以用弧长与其半径的比值来度量角的大小呢?即这个比值是否与所取的圆的半径大小无关呢? 二、弧度制定义 角度制与弧度制的互换:(1)把角度换成弧度(2)把弧度换成角度解:∵四、例题讲解 解:四、例题讲解 正角的弧度数是一个正数;
负角的弧度数是一个负数;
零角的弧度数是0.一些特殊角的弧度数 ①、弧度制是以“弧度”为单位度量角的制度,角度制是以“度”为单位度量角的制度; ②、1弧度是等于半径长的圆弧所对的圆心角(或该弧)的大小;③、不论是以“弧度”还是以“度”为单位的角的大小都是一个与半径大小无关的定值.角度制与弧度制的比较例3:计算四、例题讲解 四、例题讲解 弧长公式和扇形面积公式1、弧长公式:2、扇形面积公式:练习:1.在半径不等的两个圆内,1弧度的圆心角( )
A.所对弧长相等 B.所对的弦长相等
C.所对弧长等于各自半径 D.所对的弧长为例4:已知扇形的周长为8cm,圆心角为2弧度,求该扇形的面积.C解:设扇形的半径为r,弧长为l,则有小结我们把等于半径长的圆弧所对的圆心角叫做1弧度的角.求角的大小:
(2)方向:正角的弧度数是一个正数;
负角的弧度数是一个负数;
零角的弧度数是0.练习:求图中公路弯道处弧 的长 。
(精确到 ,图中长度单位: )解:练习2、若三角形的三个内角之比是2:3:4,求其三个内角的弧度数.1.若三角形的三个内角之比是2:3:4,求其三个内角的弧度数.
