7.2离散型随机变量及其分布列课件-2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册(共21张PPT)
文档属性
| 名称 | 7.2离散型随机变量及其分布列课件-2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-22 16:22:52 | ||
图片预览








文档简介
(共21张PPT)
7.2 离散型随机变量及其分布列
复习引入
一般地,一个试验如果满足下列条件:
①试验可以在相同的情形下重复进行;
②试验的所有可能结果是明确可知的,并且不只一个;
③每次试验总是恰好出现这些可能结果中的一个,但在一次试验之前却不能肯定这次试验会出现哪一个结果;
这种试验就是一个随机试验,为了方便起见,也简称试验.
1.随机试验的概念
我们把随机试验E的每个可能的基本结果称为样本点,全体样本点的集合称为试验E的样本空间. 我们用Ω表示样本空间,用ω表示样本点.
2.样本点与样本空间的概念
问题1:请为以下随机试验的样本点与实数建立对应关系:
(1) 掷一枚骰子,观察出现的点数;
(2) 掷两枚骰子,观察两个点数之和;
(3) 掷一枚硬币,观察出现正、反面的情况;
(4) 随机抽取一件产品,观察出现“抽到次品”和“抽到正品”的情况.
求随机事件的概率时,我们往往需要为随机试验建立样本空间,并会涉及样本点和随机事件的表示问题.类似函数在数集与数集之间建立对应关系,如果我们在随机试验的样本空间与实数集之间建立某种对应,将不仅可以为一些随机事件的表示带来方便,而且能更好地利用数学工具研究随机试验.
探究新知
有些随机试验的样本点与数值没有直接关系,我们可以根据问题的需要为每个样本点指定一个数值.
例如(3),掷一枚硬币,可将试验结果“正面朝上”用 1 表示,“反面朝上”用 0 表示,定义X=,那么这个试验的样本点与实数就建立了对应关系.
又如(4),随机抽取一件产品,如果“抽到次品”用 1 表示,“抽到正品”用 0 表示,即定义X=,那么这个试验的样本点与实数就建立了对应关系.
探究新知
有些随机试验的样本点与数值有关系,我们可以直接与实数建立对应关系.
例如(1) ,掷一枚骰子,用实数 m (m=1, 2, 3, 4, 5, 6) 表示“掷出的点数为 m”;
又如(2) ,掷两枚骰子,样本空间为 Ω={(x, y) | x, y=1, 2, , 6},用 x+y 表示“两枚骰子的点数之和”,样本点 (x, y) 就与实数 x+y 对应.
对于任何一个随机试验,总可以把它的每个样本点与一个实数对应.即通过引入一个取值依赖于样本点的变量X,来刻画样本点和实数的对应关系,实现样本点的数量化.
因为在随机试验中样本点的出现具有随机性,所以变量X的取值也具有随机性.
探究新知
考察下列随机试验及其引入的变量:
试验1:从 100 个电子元件(至少含 3 个以上次品)中随机抽取三个进行检验,变量 X 表示三个元件中的次品数;
试验2:抛掷一枚硬币直到出现正面为止,变量 Y 表示需要的抛掷次数.
这两个随机试验的样本空间各是什么?各个样本点与变量的值是如何对应的?变量 X,Y 有哪些共同的特征?
探究
探究新知
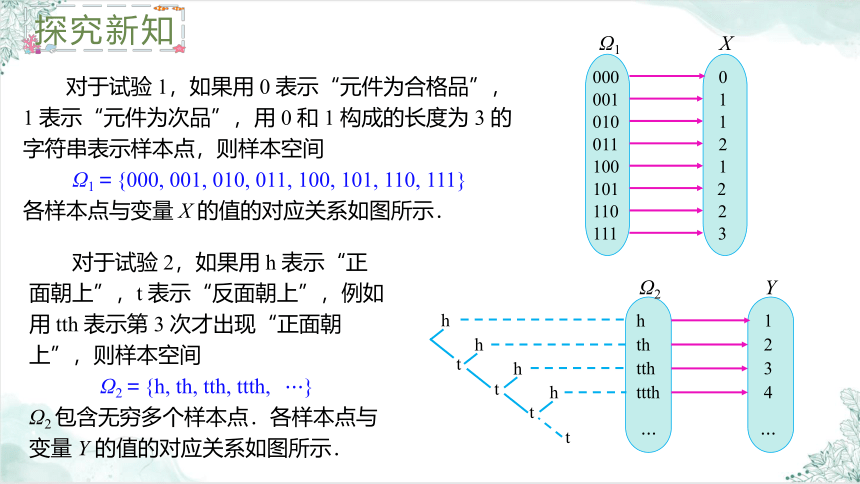
对于试验 2,如果用 h 表示“正面朝上”,t 表示“反面朝上”,例如用 tth 表示第 3 次才出现“正面朝上”,则样本空间
Ω2={h, th, tth, ttth,}
Ω2 包含无穷多个样本点.各样本点与变量 Y 的值的对应关系如图所示.
th
h
tth
ttth
t
h
h
2
1
3
4
t
h
h
Ω2
Y
t
t
探究新知
对于试验 1,如果用 0 表示“元件为合格品”,1 表示“元件为次品”,用 0 和 1 构成的长度为 3 的字符串表示样本点,则样本空间
Ω1={000, 001, 010, 011, 100, 101, 110, 111}
各样本点与变量 X 的值的对应关系如图所示.
001
000
010
011
100
101
110
111
1
0
1
2
1
2
2
3
Ω1
X
在上面两个随机试验中,每个样本点都有唯一的一个实数与之对应.
变量X,Y 有如下共同点:
(1)取值依赖于样本点;
(2)所有可能取值是明确的.
概念形成
随机变量的定义:
一般地,对于随机试验样本空间 Ω 中的每个样本点 ω,都有唯一的实数X(ω)与之对应,我们称 X 为随机变量(random variable).
说明: (1)随机变量的定义与函数的定义类似,这里的样本点 ω 相当于函数定义中的自变量,而样本空间 Ω 相当于函数的定义域.
(2)随机变量的定义与函数的定义的不同之处在于 Ω 不一定是数集.
作用:随机变量将随机事件的结果数量化.
像这样,可能取值为有限个或可以一一列举的随机变量,我们称为离散型随机变量(discrete random variable).
通常用大写英文字母表示随机变量,例如 X, Y, Z;用小写英文字母表示随机变量的取值,例如 x, y, z.
探究新知
试验 1 中随机变量X 的可能取值为 0, 1, 2, 3,共有 4 个值;
试验 2 中随机变量 Y 的可能取值为 1, 2, 3,,有无限个取值,但可以一一列举出来.
离散型随机变量的定义:
现实生活中,离散型随机变量的例子有很多.例如,某射击运动员射击一次可能命中的环数 X,它的可能取值为 0,1,2,,10;某网页在 24 h 内被浏览的次数 Y,它的可能取值为 0,1,2,;等等.
探究新知
现实生活中还有大量不是离散型随机变量的例子.例如,种子含水量的测量误差 X1;某品牌电视机的使用寿命 X2;测量某一个零件的长度产生的测量误差 X3.这些都是可能取值充满了某个区间、不能一一列举的随机变量.本节我们只研究取有限个值的离散型随机变量.
你能再举出一些离散型随机变量和不是离散型的随机变量的例子吗?
?
1.写出下列各随机变量可能的取值,并说明随机变量所取值所表示的随机试验的结果:
(1)从10张已编号的卡片(从1号到10号)中任取1张,被取出的卡片的号数X;
(2)一个袋中装有5个白球和5个黑球,从中任取3个,其中所含白球数X;
(3)抛掷两个骰子,所得点数之和X;
(4)接连不断地射击,首次命中目标需要的射击次数X;
(5)某一自动装置无故障运转的时间X;
(6)某林场树木最高达30米,此林场树木的高度X.
X=1, 2, 3, ···, n, ···
X=2, 3, 4, ···, 12
X取(0, +∞)内的一切值
X取(0, 30]内的一切值
X =1, 2, 3, ···, 10
X=0, 1, 2, 3
离散型
连续型
小试牛刀
根据问题引入合适的随机变量,有利于我们简洁地表示所关心的随机事件,并利用数学工具研究随机试验中的概率问题.
例如,掷一枚质地均匀的骰子,X 表示掷出的点数,则事件“掷出 m 点”可以表示为 {X=m} (m=1, 2, 3, 4, 5, 6),事件“掷出的点数不大于 2”可以表示为 {X≤2},事件“掷出偶数点”可以表示为 {X=2}∪{X=4}∪{X=6},等等.
由掷出各种点数的等可能性,可得
P(X=m)=,m= 1, 2, 3, 4, 5, 6 .
这一规律可以用下表来表示,也可以用下图来表示.
探究新知
2
1
3
4
5
6
X
P
P
X
1
0
2
3
4
5
6
一般地,设离散型随机变量 X 的可能取值为 x1, x2,, xn,我们称 X 取每一个值 xi 的概率
P(X=xi)=pi,i=1, 2,, n
为 X 的概率分布列(list of probability distribution),简称分布列.
探究新知
分布列的定义:
1.分布列的构成
(1)列出了随机变量X的所有取值xi;
(2)求出了的每一个取值xi的概率pi .
2.分布列的性质:
(1) pi≥0,i=1,2,,n;
(2) p1+p2+ +pn=1.
注意:
由于函数可以用解析式、表格、图象表示,所以离散型随机变量的分布列也可以用解析式、表格、图象表示.
分布列的表示:
探究新知
P(X=xi)=pi,i=1, 2,, n
1.解析式法
x2
x1
xn
X
P
p2
p1
pn
2.表格法
3.图象法
P
X
x1
0
x2
x3
xn
p3
p1
pn
p2
利用分布列和概率的性质,可以计算由离散型随机变量表示的事件的概率.
例如,在掷骰子试验中,由概率的加法公式,得事件“掷出的点数不大于2”的概率为
P(X≤2)=P(X=1)+P(X=2)=+=.
类似地,事件“掷出偶数点”的概率为
P({X=2}∪{X=4}∪{X=6})=P(X=2)+P(X=4)+P(X=6)=++=.
探究新知
例1 一批产品中次品率为 5%,随机抽取 1 件,定义
X =,
求 X 的分布列.
典例分析
解:根据 X 的定义,{X=1}=“抽到次品”,{X=0}=“抽到正品”,
X 的分布列为
P(X=0)=0.95,P(X=1)=0.05.
1
0
X
P
0.05
0.95
用表格表示 X 的分布列,如下表所示.
对于只有两个可能结果的随机试验,用 A 表示“成功”, 表示“失败”,定义 X= . 如果 P(A)=p,则 P()=1-p,那么 X 的分布列如下表所示.
1
0
X
P
p
1-p
我们称 X 服从两点分布(two-point distribution)或 0-1分布.
探究新知
两点分布的定义:
X 2 3
P 0.3 0.7
思考:随机变量X的分布列由下表给出, 它服从两点分布吗
注: 只取两个不同值的随机变量并不一定服从两点分布
不服从两点分布, 因为X的取值不是0或1
例2 某学校高二年级有 200 名学生,他们的体育综合测试成绩分 5 个等级,每个等级对应的分数和人数如下表所示.
从这200名学生中任意选取1人,求所选同学分数X的分布列,以及 P(X≥4).
2
1
3
4
5
不及格
等级
分数
50
20
60
40
30
人数
及格
中等
良
优
典例分析
解:由题意知,X 是一个离散型随机变量,其可能取值为 1, 2, 3, 4, 5,且{X=1}=“不及格”,{X=2}=“及格”,{X=3}=“中等”,{X=4}=“良”,{X=5}=“优”.根据古典概型的知识,可得 X 的分布列,如下表所示.
2
1
3
4
5
X
P
P(X≥4)=P(X=4)+P(X=5)=+=.
解:设挑选的 2 台电脑中 A 品牌的台数为 X,则 X 的可能取值为 0, 1, 2.
根据古典概型的知识,可得 X 的分布列为
P(X=0)==,P(X=1)==,P(X=2)==.
用表格表示 X 的分布列,如下表所示.
1
0
2
X
P
典例分析
例3 一批笔记本电脑共有 10 台,其中 A 品牌 3 台,B 品牌 7 台.如果从中随机挑选 2 台,求这 2 台电脑中 A 品牌台数的分布列.
1.篮球比赛中每次罚球命中得 1 分,不中得 0 分.已知某运动员罚球命中的概率为 0.7,求他一次罚球得分的分布列.
1
0
X
P
0.7
0.3
2.抛掷一枚质地均匀的硬币 2 次,写出正面向上次数 X 的分布列.
1
0
2
X
P
巩固练习
离散型随机变量及其分布
两点分布或0—1 分布
随机变量
离散型随机变量
分布列
课堂小结
7.2 离散型随机变量及其分布列
复习引入
一般地,一个试验如果满足下列条件:
①试验可以在相同的情形下重复进行;
②试验的所有可能结果是明确可知的,并且不只一个;
③每次试验总是恰好出现这些可能结果中的一个,但在一次试验之前却不能肯定这次试验会出现哪一个结果;
这种试验就是一个随机试验,为了方便起见,也简称试验.
1.随机试验的概念
我们把随机试验E的每个可能的基本结果称为样本点,全体样本点的集合称为试验E的样本空间. 我们用Ω表示样本空间,用ω表示样本点.
2.样本点与样本空间的概念
问题1:请为以下随机试验的样本点与实数建立对应关系:
(1) 掷一枚骰子,观察出现的点数;
(2) 掷两枚骰子,观察两个点数之和;
(3) 掷一枚硬币,观察出现正、反面的情况;
(4) 随机抽取一件产品,观察出现“抽到次品”和“抽到正品”的情况.
求随机事件的概率时,我们往往需要为随机试验建立样本空间,并会涉及样本点和随机事件的表示问题.类似函数在数集与数集之间建立对应关系,如果我们在随机试验的样本空间与实数集之间建立某种对应,将不仅可以为一些随机事件的表示带来方便,而且能更好地利用数学工具研究随机试验.
探究新知
有些随机试验的样本点与数值没有直接关系,我们可以根据问题的需要为每个样本点指定一个数值.
例如(3),掷一枚硬币,可将试验结果“正面朝上”用 1 表示,“反面朝上”用 0 表示,定义X=,那么这个试验的样本点与实数就建立了对应关系.
又如(4),随机抽取一件产品,如果“抽到次品”用 1 表示,“抽到正品”用 0 表示,即定义X=,那么这个试验的样本点与实数就建立了对应关系.
探究新知
有些随机试验的样本点与数值有关系,我们可以直接与实数建立对应关系.
例如(1) ,掷一枚骰子,用实数 m (m=1, 2, 3, 4, 5, 6) 表示“掷出的点数为 m”;
又如(2) ,掷两枚骰子,样本空间为 Ω={(x, y) | x, y=1, 2, , 6},用 x+y 表示“两枚骰子的点数之和”,样本点 (x, y) 就与实数 x+y 对应.
对于任何一个随机试验,总可以把它的每个样本点与一个实数对应.即通过引入一个取值依赖于样本点的变量X,来刻画样本点和实数的对应关系,实现样本点的数量化.
因为在随机试验中样本点的出现具有随机性,所以变量X的取值也具有随机性.
探究新知
考察下列随机试验及其引入的变量:
试验1:从 100 个电子元件(至少含 3 个以上次品)中随机抽取三个进行检验,变量 X 表示三个元件中的次品数;
试验2:抛掷一枚硬币直到出现正面为止,变量 Y 表示需要的抛掷次数.
这两个随机试验的样本空间各是什么?各个样本点与变量的值是如何对应的?变量 X,Y 有哪些共同的特征?
探究
探究新知
对于试验 2,如果用 h 表示“正面朝上”,t 表示“反面朝上”,例如用 tth 表示第 3 次才出现“正面朝上”,则样本空间
Ω2={h, th, tth, ttth,}
Ω2 包含无穷多个样本点.各样本点与变量 Y 的值的对应关系如图所示.
th
h
tth
ttth
t
h
h
2
1
3
4
t
h
h
Ω2
Y
t
t
探究新知
对于试验 1,如果用 0 表示“元件为合格品”,1 表示“元件为次品”,用 0 和 1 构成的长度为 3 的字符串表示样本点,则样本空间
Ω1={000, 001, 010, 011, 100, 101, 110, 111}
各样本点与变量 X 的值的对应关系如图所示.
001
000
010
011
100
101
110
111
1
0
1
2
1
2
2
3
Ω1
X
在上面两个随机试验中,每个样本点都有唯一的一个实数与之对应.
变量X,Y 有如下共同点:
(1)取值依赖于样本点;
(2)所有可能取值是明确的.
概念形成
随机变量的定义:
一般地,对于随机试验样本空间 Ω 中的每个样本点 ω,都有唯一的实数X(ω)与之对应,我们称 X 为随机变量(random variable).
说明: (1)随机变量的定义与函数的定义类似,这里的样本点 ω 相当于函数定义中的自变量,而样本空间 Ω 相当于函数的定义域.
(2)随机变量的定义与函数的定义的不同之处在于 Ω 不一定是数集.
作用:随机变量将随机事件的结果数量化.
像这样,可能取值为有限个或可以一一列举的随机变量,我们称为离散型随机变量(discrete random variable).
通常用大写英文字母表示随机变量,例如 X, Y, Z;用小写英文字母表示随机变量的取值,例如 x, y, z.
探究新知
试验 1 中随机变量X 的可能取值为 0, 1, 2, 3,共有 4 个值;
试验 2 中随机变量 Y 的可能取值为 1, 2, 3,,有无限个取值,但可以一一列举出来.
离散型随机变量的定义:
现实生活中,离散型随机变量的例子有很多.例如,某射击运动员射击一次可能命中的环数 X,它的可能取值为 0,1,2,,10;某网页在 24 h 内被浏览的次数 Y,它的可能取值为 0,1,2,;等等.
探究新知
现实生活中还有大量不是离散型随机变量的例子.例如,种子含水量的测量误差 X1;某品牌电视机的使用寿命 X2;测量某一个零件的长度产生的测量误差 X3.这些都是可能取值充满了某个区间、不能一一列举的随机变量.本节我们只研究取有限个值的离散型随机变量.
你能再举出一些离散型随机变量和不是离散型的随机变量的例子吗?
?
1.写出下列各随机变量可能的取值,并说明随机变量所取值所表示的随机试验的结果:
(1)从10张已编号的卡片(从1号到10号)中任取1张,被取出的卡片的号数X;
(2)一个袋中装有5个白球和5个黑球,从中任取3个,其中所含白球数X;
(3)抛掷两个骰子,所得点数之和X;
(4)接连不断地射击,首次命中目标需要的射击次数X;
(5)某一自动装置无故障运转的时间X;
(6)某林场树木最高达30米,此林场树木的高度X.
X=1, 2, 3, ···, n, ···
X=2, 3, 4, ···, 12
X取(0, +∞)内的一切值
X取(0, 30]内的一切值
X =1, 2, 3, ···, 10
X=0, 1, 2, 3
离散型
连续型
小试牛刀
根据问题引入合适的随机变量,有利于我们简洁地表示所关心的随机事件,并利用数学工具研究随机试验中的概率问题.
例如,掷一枚质地均匀的骰子,X 表示掷出的点数,则事件“掷出 m 点”可以表示为 {X=m} (m=1, 2, 3, 4, 5, 6),事件“掷出的点数不大于 2”可以表示为 {X≤2},事件“掷出偶数点”可以表示为 {X=2}∪{X=4}∪{X=6},等等.
由掷出各种点数的等可能性,可得
P(X=m)=,m= 1, 2, 3, 4, 5, 6 .
这一规律可以用下表来表示,也可以用下图来表示.
探究新知
2
1
3
4
5
6
X
P
P
X
1
0
2
3
4
5
6
一般地,设离散型随机变量 X 的可能取值为 x1, x2,, xn,我们称 X 取每一个值 xi 的概率
P(X=xi)=pi,i=1, 2,, n
为 X 的概率分布列(list of probability distribution),简称分布列.
探究新知
分布列的定义:
1.分布列的构成
(1)列出了随机变量X的所有取值xi;
(2)求出了的每一个取值xi的概率pi .
2.分布列的性质:
(1) pi≥0,i=1,2,,n;
(2) p1+p2+ +pn=1.
注意:
由于函数可以用解析式、表格、图象表示,所以离散型随机变量的分布列也可以用解析式、表格、图象表示.
分布列的表示:
探究新知
P(X=xi)=pi,i=1, 2,, n
1.解析式法
x2
x1
xn
X
P
p2
p1
pn
2.表格法
3.图象法
P
X
x1
0
x2
x3
xn
p3
p1
pn
p2
利用分布列和概率的性质,可以计算由离散型随机变量表示的事件的概率.
例如,在掷骰子试验中,由概率的加法公式,得事件“掷出的点数不大于2”的概率为
P(X≤2)=P(X=1)+P(X=2)=+=.
类似地,事件“掷出偶数点”的概率为
P({X=2}∪{X=4}∪{X=6})=P(X=2)+P(X=4)+P(X=6)=++=.
探究新知
例1 一批产品中次品率为 5%,随机抽取 1 件,定义
X =,
求 X 的分布列.
典例分析
解:根据 X 的定义,{X=1}=“抽到次品”,{X=0}=“抽到正品”,
X 的分布列为
P(X=0)=0.95,P(X=1)=0.05.
1
0
X
P
0.05
0.95
用表格表示 X 的分布列,如下表所示.
对于只有两个可能结果的随机试验,用 A 表示“成功”, 表示“失败”,定义 X= . 如果 P(A)=p,则 P()=1-p,那么 X 的分布列如下表所示.
1
0
X
P
p
1-p
我们称 X 服从两点分布(two-point distribution)或 0-1分布.
探究新知
两点分布的定义:
X 2 3
P 0.3 0.7
思考:随机变量X的分布列由下表给出, 它服从两点分布吗
注: 只取两个不同值的随机变量并不一定服从两点分布
不服从两点分布, 因为X的取值不是0或1
例2 某学校高二年级有 200 名学生,他们的体育综合测试成绩分 5 个等级,每个等级对应的分数和人数如下表所示.
从这200名学生中任意选取1人,求所选同学分数X的分布列,以及 P(X≥4).
2
1
3
4
5
不及格
等级
分数
50
20
60
40
30
人数
及格
中等
良
优
典例分析
解:由题意知,X 是一个离散型随机变量,其可能取值为 1, 2, 3, 4, 5,且{X=1}=“不及格”,{X=2}=“及格”,{X=3}=“中等”,{X=4}=“良”,{X=5}=“优”.根据古典概型的知识,可得 X 的分布列,如下表所示.
2
1
3
4
5
X
P
P(X≥4)=P(X=4)+P(X=5)=+=.
解:设挑选的 2 台电脑中 A 品牌的台数为 X,则 X 的可能取值为 0, 1, 2.
根据古典概型的知识,可得 X 的分布列为
P(X=0)==,P(X=1)==,P(X=2)==.
用表格表示 X 的分布列,如下表所示.
1
0
2
X
P
典例分析
例3 一批笔记本电脑共有 10 台,其中 A 品牌 3 台,B 品牌 7 台.如果从中随机挑选 2 台,求这 2 台电脑中 A 品牌台数的分布列.
1.篮球比赛中每次罚球命中得 1 分,不中得 0 分.已知某运动员罚球命中的概率为 0.7,求他一次罚球得分的分布列.
1
0
X
P
0.7
0.3
2.抛掷一枚质地均匀的硬币 2 次,写出正面向上次数 X 的分布列.
1
0
2
X
P
巩固练习
离散型随机变量及其分布
两点分布或0—1 分布
随机变量
离散型随机变量
分布列
课堂小结
