江苏省涟水金城外国语学校2013届高三下学期期初检测数学试题
文档属性
| 名称 | 江苏省涟水金城外国语学校2013届高三下学期期初检测数学试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 622.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-05 00:00:00 | ||
图片预览


文档简介
一、填空题
1.原点到直线的距离等于
2.已知实数满足,则的最大值为21,则 _____
3.已知点在直线上,则的最小值为 .
4.两个整数490和910的最大公约数是 ▲ .
5.已知向量,满足·=0,││=1,││=2,则│2-│=_________。
6.若的内角满足,则_______
7.设满足条件若函数的最大值为8,则的最小值为
8.已知不等式组的整数解只有1,则实数的取值范围是 .
9.已知
10.如图,已知是圆的直径,,为圆上任意一点,过点做圆的切线分别与过两点的切线交于点,则________________.
11.不等式的解集是
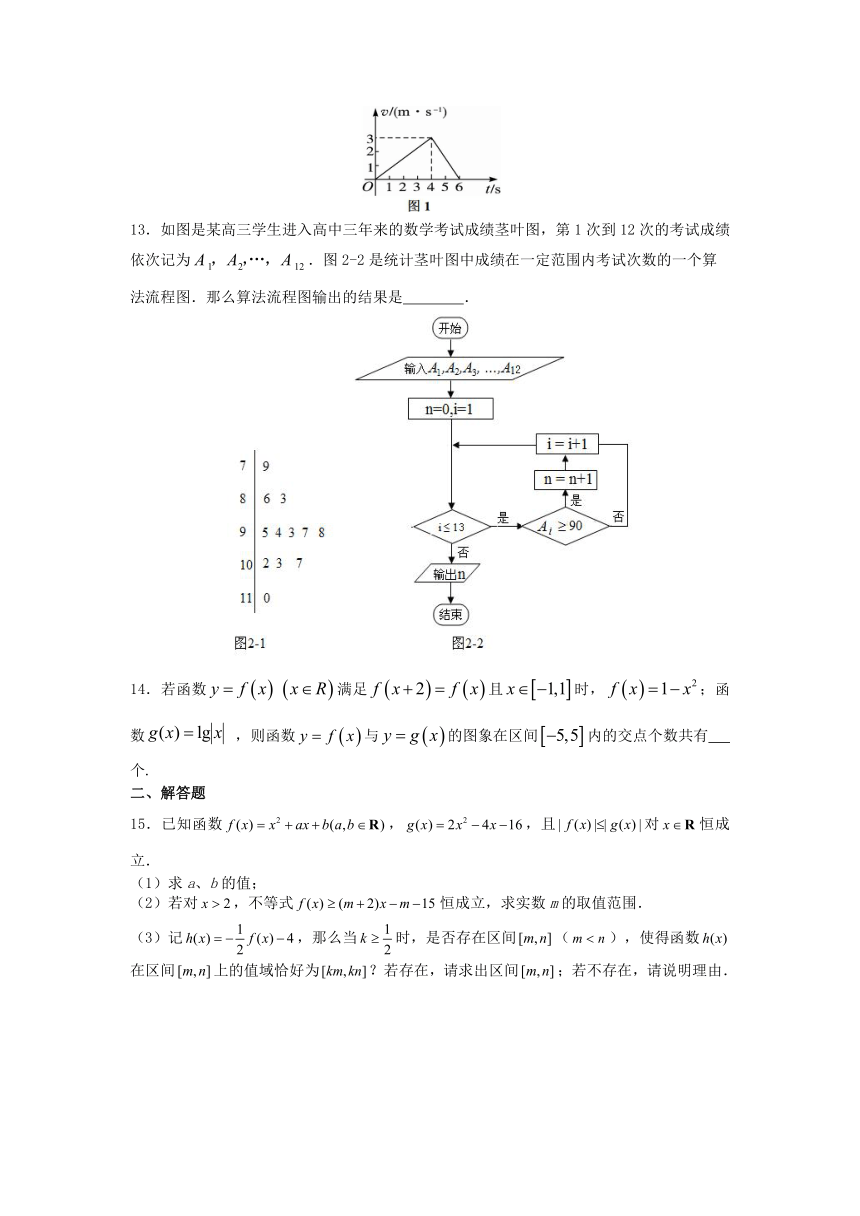
12.如图是一个质点做直线运动的图象,则质点在前内的位移为 m
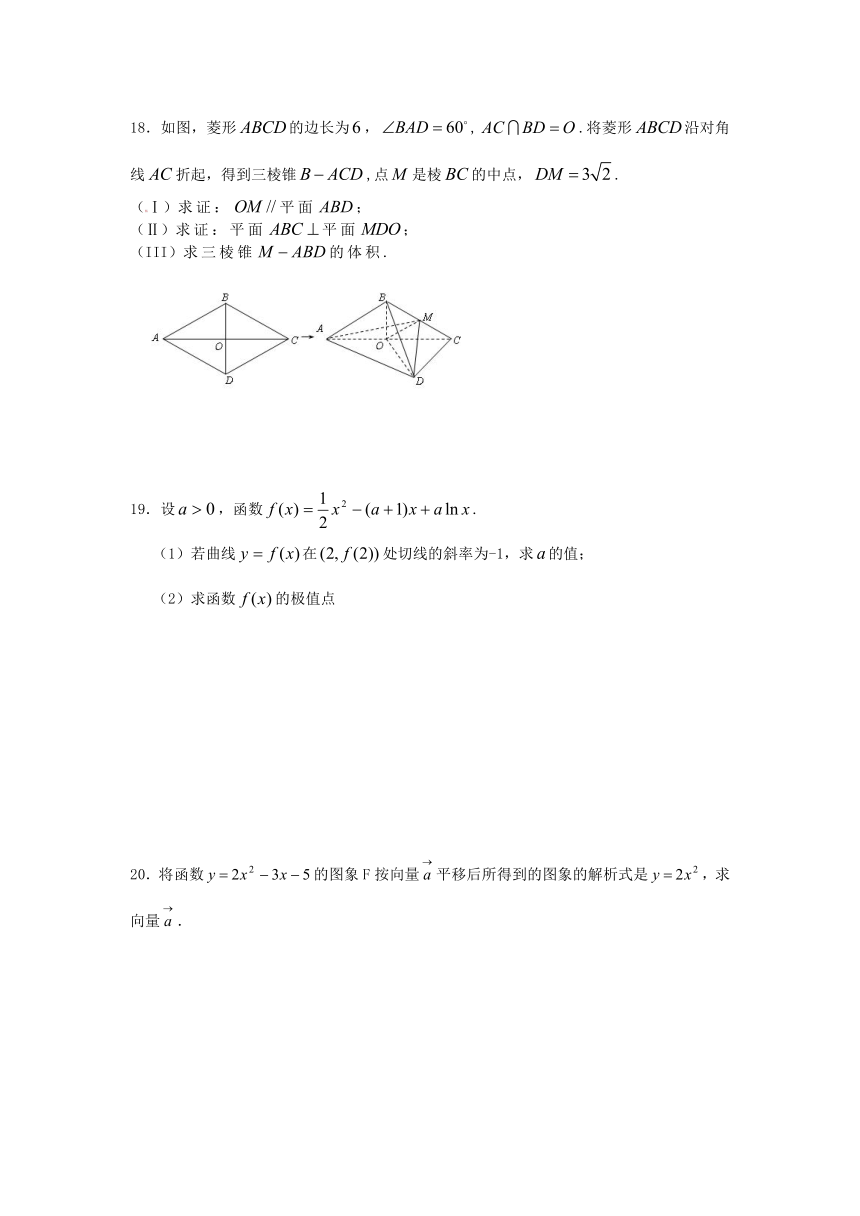
13.如图是某高三学生进入高中三年来的数学考试成绩茎叶图,第1次到12次的考试成绩依次记为.图2-2是统计茎叶图中成绩在一定范围内考试次数的一个算
法流程图.那么算法流程图输出的结果是 .
14.若函数满足且时,;函数 ,则函数与的图象在区间内的交点个数共有
个.
二、解答题
15.已知函数,,且对恒成立.
(1)求a、b的值;
(2)若对,不等式恒成立,求实数m的取值范围.
(3)记,那么当时,是否存在区间(),使得函数在区间上的值域恰好为?若存在,请求出区间;若不存在,请说明理由.
16.某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上每隔1小时抽一包产品,称其重量(单位:克)是否合格,分别记录了6个抽查数据,获得重量数据的茎叶图如图4.
根据样品数据,计算甲、乙两个车间产品重量的均值与方差,并说明哪个车间的产品的重量相对较稳定;
若从乙车间6件样品中随机抽取两件,求所抽取的两件样品的重量之差不超过2克的概率.
17. 求在上,由轴及正弦曲线围成的图形的面积.
18.如图,菱形的边长为,,.将菱形沿对角线折起,得到三棱锥,点是棱的中点,.
(Ⅰ)求证:平面;
(Ⅱ)求证:平面平面;
(III)求三棱锥的体积.
19.设,函数.
(1)若曲线在处切线的斜率为-1,求的值;
(2)求函数的极值点
20.将函数的图象F按向量平移后所得到的图象的解析式是,求向量.
参考答案
1.
2.或
3.4
4.70
5.
6.
7.4
8.
9.
10.
11.
12.9
13.9
14.8
15.解.令,则对有解.
记,则或解得.
解析:( 1)由得或.于是,当或时,得
∴∴此时,,对恒成立,满足条件.故.
(2)∵对恒成立,∴对恒成立.
记.∵,∴,∴由对勾函数在上的图象知当,即时,,∴.
(3)∵,∴,∴,又∵,∴,∴,∴在上是单调增函数,∴即即∵,且,故:当时,;当时,;当时,不存在.
16.(1)甲车间的产品的重量相对较稳定. (2) .
(1)先计算平均数,平均数差距不大的情况下,再计算方差,方差越小,发挥越稳定.
(2)本不题属于古典概型.先列出乙车间6件样品中随机抽取两件共有15种基本结果,然后再把事件“所抽取的两件样品的重量之差不超过2克”包含的基本结果列出来,再根据古典概型概率计算公式求解即可
(1) , …… 1分
, …… 2分
=21,
,4分
∵, , …… 5分
∴甲车间的产品的重量相对较稳定. …… 6分
(2) 从乙车间6件样品中随机抽取两件,共有15种不同的取法:
… 8分
设表示随机事件“所抽取的两件样品的重量之差不超过2克”,则的基本事件有4种:,. …… 10分
故所求概率为.
17.4
因为在上,,其图象在轴上方;在上,其图象在轴下方,此时定积分为图形面积的相反数,应加绝对值才表示面积.作出在上的图象如下图所示, 与轴交于0、、,,所求
18.证明:(Ⅰ)因为点是菱形的对角线的交点,所以是的中点.又点是棱的中点,所以是的中位线,. ………………………… 2分
因为平面,平面,所以平面. …………………4分
(Ⅱ)由题意,,
因为,所以,. …………………………….6分
又因为菱形,所以.
因为,所以平面,
因为平面,所以平面平面.
……………………………………………………………….9分
(Ⅲ)三棱锥的体积等于三棱锥的体积.
由(Ⅱ)知,平面,所以为三棱锥的高,且.
的面积为.
所求体积等于. ………………………………………………12分
19.(Ⅰ) (Ⅱ)当时,是的极大值点,是的极小值点;当时,没有极值点;当时,是的极大值点,是的极小值点
(1)由已知 2分
4分
曲线在处切线的斜率为-1,所以 5分
即,所以 6分
(2) 8分
①当时,
当时,,函数单调递增;
当时,,函数单调递减;
当时,,函数单调递增。
此时是的极大值点,是的极小值点 10分
②当时,
当时,>0,
当时,,
当时,
所以函数在定义域内单调递增,此时没有极值点 11分
③当时,[来源:]
当时,,函数单调递增;
当时,,函数单调递减;
当时,,函数单调递增
此时是的极大值点,
是的极小值点 13分
综上,当时,是的极大值点,是的极小值点;
当时,没有极值点;
当时,是的极大值点,是的极小值点
20.向量
设向量,将F按向量平移所得到的图象F,的解析式是
,
化简整理得,
依题意,这一函数即为,
∴解得
故所求的向量.
同课章节目录
