4.1功 课件 物理教科版必修2 (25张PPT)
文档属性
| 名称 | 4.1功 课件 物理教科版必修2 (25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-21 15:52:21 | ||
图片预览




文档简介
(共25张PPT)
第四章 机械能和能源
4.1 功
举起杠铃
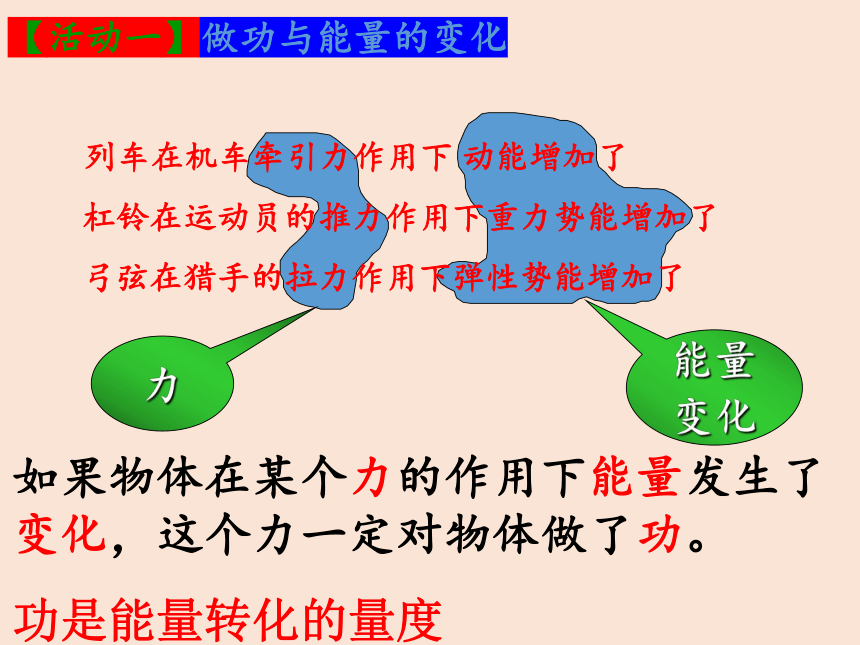
【活动一】做功与能量的变化
弯
弓
射
箭
列
车
启
动
问题1:能量的转化通过什么实现?能量的变化用什么来量度?两者之间有什么联系?
能量变化
力
如果物体在某个力的作用下能量发生了变化,这个力一定对物体做了功。
功是能量转化的量度
列车在机车牵引力作用下 动能增加了
杠铃在运动员的推力作用下重力势能增加了
弓弦在猎手的拉力作用下弹性势能增加了
【活动一】做功与能量的变化
小球在桌面上滚动时,重力和桌面对小球的支持力对小球做功吗?
力对物体做功的因素是什么?
议一议
问题2:做功的两个必要因素?
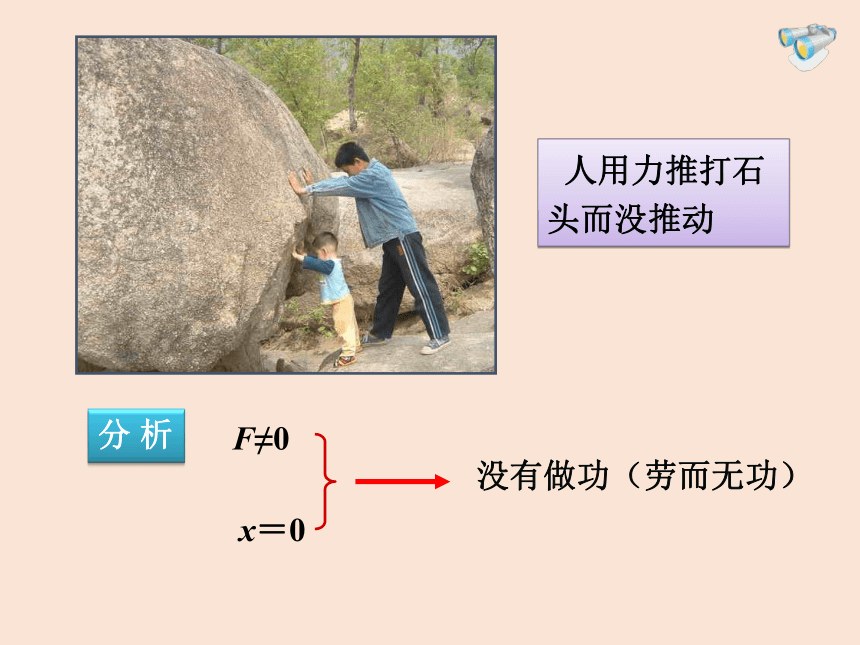
没有做功(劳而无功)
人用力推打石头而没推动
x=0
F≠0
分 析
没有做功(不劳无功)
分 析
x ≠ 0
F = 0
冰壶在平滑(平而光滑)的冰面上滑行
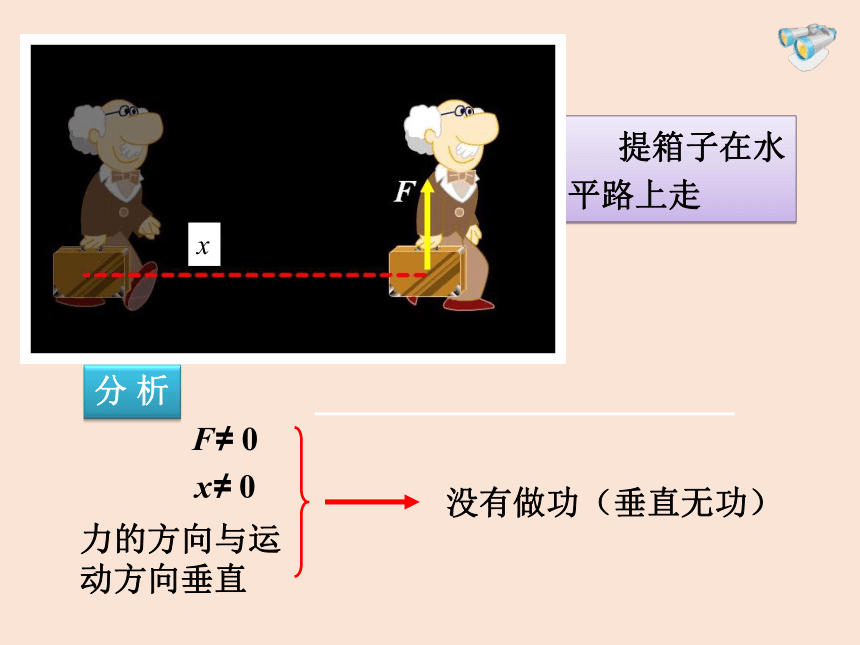
没有做功(垂直无功)
提箱子在水平路上走
分 析
F≠ 0
x≠ 0
力的方向与运动方向垂直
x
x
F
F
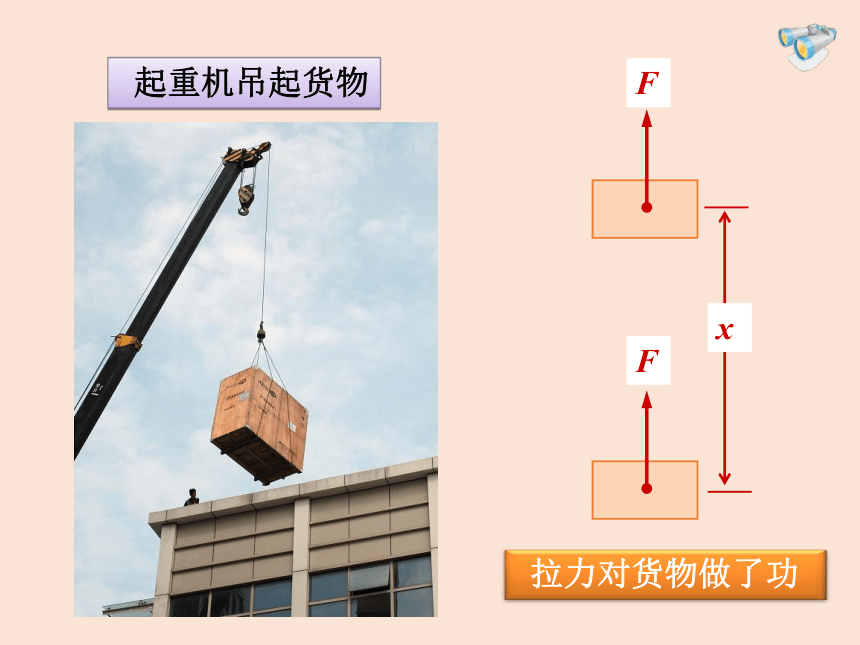
起重机吊起货物
拉力对货物做了功
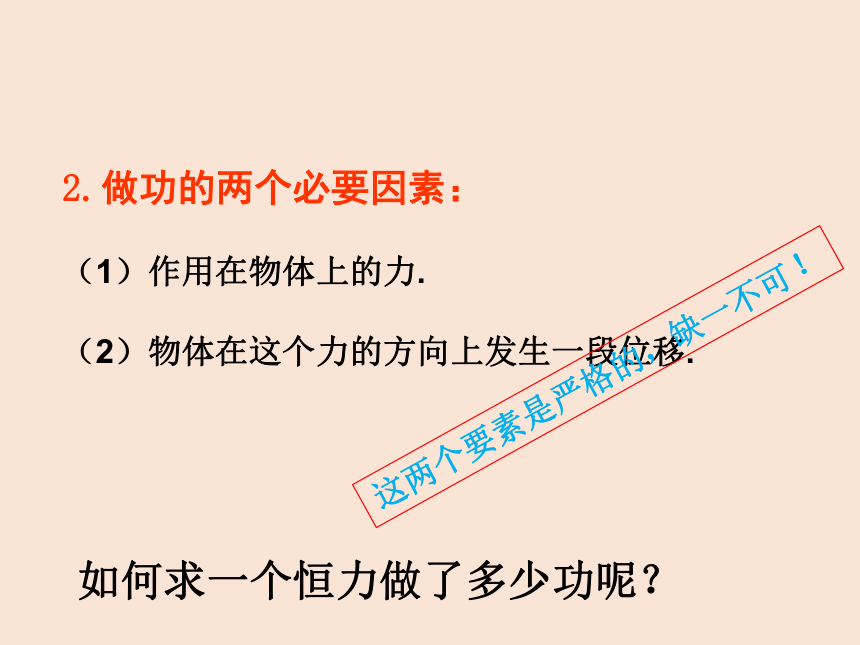
2.做功的两个必要因素:
(1)作用在物体上的力.
(2)物体在这个力的方向上发生一段位移.
这两个要素是严格的,缺一不可 !
如何求一个恒力做了多少功呢?
【活动二】功的计算
【情景】如图,一个箱子在水平恒定推力F作用下沿水平面运动了距离L。
问题3:结合初中所学功的知识,计算箱子受到的推力、重力、支持力对箱子各做了多少功?
问题4:如图所示,如果将水平恒定推力改成斜向
上与水平面成 角的拉力,又该如何计算拉力对
箱子做的功呢?
F
结论:
l
F
F⊥
F∥
F
其中 为力的方向与位移的方向之间的夹角
方案1:分解力
结论:
F
l
l⊥
l ∥
F
其中 为力的方向与位移的方向之间的夹角
方案2:分解位移
问题5:归纳功的计算公式及分析应用时注意点?
(1)力对物体做的功,等于力的“大小” ,位移的“大小” 、“力与位移夹角余弦” 这三者的乘积。
(2)单位:焦耳,符号——J。
(5)功是“标量” (没有方向)。
(4)功是“过程量”(是力对位移积累的过程)。
(3)公式适用条件:一般只适用于计算“恒力” 做功。
【活动二】功的计算
【例题1】如图,物体在力F的作用下在水平面上发生了一段位移L,分别计算这三种情形下力F对物体做的功。设这三种情形下力和位移的大小都相同F=10N,L=2m。θ的大小如图所示。
解题规范提醒:去伪存真。
【活动三】功的正负
问题6:用公式 计算功,结果肯定会出现负值,负功有没有意义
【讨论——如何判断力对物体做正功还是做负功】
【特别提醒】
某力对物体“做多少负功”
也可以说成:物体“克服” 这个力做多少“正功” (取绝对值)。
③当 时,力对物体不做功。
②当 时,力对物体做负功。
①当 时,力对物体做正功。
解题规范提醒:看清楚题目是否问“克服某个力做功”。
对功的“正负” 的理解:
(1)不表示功的方向。
功是标量,没有方向。
(2)不表示功的大小。
某力在某过程中对物体做正功,表示该力是动力。
某力在某过程中对物体做负功,表示该力是阻力。
(4)功的正、负反映了能量转化的方向。
正功
通过该力做功 将其它形式的能转化为动能。
负功
通过该力做功 将动能转化为其它形式的能。
(3)功的正、负反映了做功的力的作用效果。
【例题2】用起重机把重为2×104N的货物匀速提升5m,钢绳的拉力做功 J,重力做功 J,钢绳克服重力做功 J。
【例题3】一个人从4m深的水井中匀速提取50N的水桶至地面,又提着水桶在水平道路上行走12m,再匀速走下4m深的地下室,则此人提水桶的力所做的功为 。
【活动三】功的正负
1×105
-1×105
1×105
0
你如何得出整个过程中拉力做的功?
功是标量,一个力在不同过程做的功可直接相加“求代数和” 。
1.分别求出每个力所做的功,然后求出所有功的代数和.
即:W总=W1+W2+……+Wn
2.先求出物体所受的合力,然后再求出合力的功.
即:W总=F合xcosα
【活动四】合力的功(总功)
功的累积性
提醒:方法2仅适用于几个力同时作用于物体的情况,因为只有当这几个力同时作用于物体上时,才能求出它们的合力;方法1则不管几个力同时作用,还是作用时间有先后均适用.
例题4:质量为m=3kg的物体放在水平面上,在与水平方向成370角的拉力F=20N作用下匀加速运动,通过位移 S=2m的过程中,物体所受摩擦力大小为6N。(cos370=0.8)求:
WG=0J
WN=0J
Wf =-f S=-12J
W总=WG+WN +Wf +WF=20J
(1)重力对物体做的功
(2)支持力对物体做的功
(3)摩擦力对物体做的功
(4)拉力对物体做的功
(5)合力对物体做的功
W总=F合S=20J
方法一
方法二
WF=FScos370=32J
W总=20J
F
N
G
f
α
【活动四】合力的功
【活动五】变力的功
问题7:恒力做功可以利用公式计算,那么怎样处理变力做功的问题
【微元法】
【例题5】如图所示,一物体在力F的作用下,沿半径为R的圆周绕行一周,若力F的大小保持不变,方向始终沿圆周的切线方向,则力F做了多少功
将物理过程分割成许多个微小的单元,从而达到“化曲为直、化变为恒”的效果,方便分析求解。
将圆周分成很多小段,每一小段小到能将弧线视作直线,力F视作恒力,则在某一微元上,力F所做的功可表示为: , ,·······
因为:
所以:
化曲为直
化变为恒
【图像法】
问题8:如图所示,物块在F=10N水平恒定推力作用下运动了L=10m,力F对物块做的功除了利用公式计算,还有其他方法吗
类比v—t图像的“面积” 可以计算变加速运动的位移。
面积大小表示力F做的功大小(体现了力对位移的累积思想)。
【思考题】如图(a),一质量为m=1kg的滑块(可视为质点)以初速度v0沿水平方向从A滑到B,已知滑块与水平面间的动摩擦因数μ和滑块到A点的距离x的关系如图(b),求摩擦力做的功。
计算面积
(a)
(b)
1.如果物体在某个力的作用下能量发生了变化,这个力一定对物体做了功。功是能量转化的量度
2.做功的两个必要因素:
(1)作用在物体上的力.
(2)物体在这个力的方向上发生一段位移.
3.对公式的理解
W总=W1+W2+……+Wn
作业:练习册
谢 谢
第四章 机械能和能源
4.1 功
举起杠铃
【活动一】做功与能量的变化
弯
弓
射
箭
列
车
启
动
问题1:能量的转化通过什么实现?能量的变化用什么来量度?两者之间有什么联系?
能量变化
力
如果物体在某个力的作用下能量发生了变化,这个力一定对物体做了功。
功是能量转化的量度
列车在机车牵引力作用下 动能增加了
杠铃在运动员的推力作用下重力势能增加了
弓弦在猎手的拉力作用下弹性势能增加了
【活动一】做功与能量的变化
小球在桌面上滚动时,重力和桌面对小球的支持力对小球做功吗?
力对物体做功的因素是什么?
议一议
问题2:做功的两个必要因素?
没有做功(劳而无功)
人用力推打石头而没推动
x=0
F≠0
分 析
没有做功(不劳无功)
分 析
x ≠ 0
F = 0
冰壶在平滑(平而光滑)的冰面上滑行
没有做功(垂直无功)
提箱子在水平路上走
分 析
F≠ 0
x≠ 0
力的方向与运动方向垂直
x
x
F
F
起重机吊起货物
拉力对货物做了功
2.做功的两个必要因素:
(1)作用在物体上的力.
(2)物体在这个力的方向上发生一段位移.
这两个要素是严格的,缺一不可 !
如何求一个恒力做了多少功呢?
【活动二】功的计算
【情景】如图,一个箱子在水平恒定推力F作用下沿水平面运动了距离L。
问题3:结合初中所学功的知识,计算箱子受到的推力、重力、支持力对箱子各做了多少功?
问题4:如图所示,如果将水平恒定推力改成斜向
上与水平面成 角的拉力,又该如何计算拉力对
箱子做的功呢?
F
结论:
l
F
F⊥
F∥
F
其中 为力的方向与位移的方向之间的夹角
方案1:分解力
结论:
F
l
l⊥
l ∥
F
其中 为力的方向与位移的方向之间的夹角
方案2:分解位移
问题5:归纳功的计算公式及分析应用时注意点?
(1)力对物体做的功,等于力的“大小” ,位移的“大小” 、“力与位移夹角余弦” 这三者的乘积。
(2)单位:焦耳,符号——J。
(5)功是“标量” (没有方向)。
(4)功是“过程量”(是力对位移积累的过程)。
(3)公式适用条件:一般只适用于计算“恒力” 做功。
【活动二】功的计算
【例题1】如图,物体在力F的作用下在水平面上发生了一段位移L,分别计算这三种情形下力F对物体做的功。设这三种情形下力和位移的大小都相同F=10N,L=2m。θ的大小如图所示。
解题规范提醒:去伪存真。
【活动三】功的正负
问题6:用公式 计算功,结果肯定会出现负值,负功有没有意义
【讨论——如何判断力对物体做正功还是做负功】
【特别提醒】
某力对物体“做多少负功”
也可以说成:物体“克服” 这个力做多少“正功” (取绝对值)。
③当 时,力对物体不做功。
②当 时,力对物体做负功。
①当 时,力对物体做正功。
解题规范提醒:看清楚题目是否问“克服某个力做功”。
对功的“正负” 的理解:
(1)不表示功的方向。
功是标量,没有方向。
(2)不表示功的大小。
某力在某过程中对物体做正功,表示该力是动力。
某力在某过程中对物体做负功,表示该力是阻力。
(4)功的正、负反映了能量转化的方向。
正功
通过该力做功 将其它形式的能转化为动能。
负功
通过该力做功 将动能转化为其它形式的能。
(3)功的正、负反映了做功的力的作用效果。
【例题2】用起重机把重为2×104N的货物匀速提升5m,钢绳的拉力做功 J,重力做功 J,钢绳克服重力做功 J。
【例题3】一个人从4m深的水井中匀速提取50N的水桶至地面,又提着水桶在水平道路上行走12m,再匀速走下4m深的地下室,则此人提水桶的力所做的功为 。
【活动三】功的正负
1×105
-1×105
1×105
0
你如何得出整个过程中拉力做的功?
功是标量,一个力在不同过程做的功可直接相加“求代数和” 。
1.分别求出每个力所做的功,然后求出所有功的代数和.
即:W总=W1+W2+……+Wn
2.先求出物体所受的合力,然后再求出合力的功.
即:W总=F合xcosα
【活动四】合力的功(总功)
功的累积性
提醒:方法2仅适用于几个力同时作用于物体的情况,因为只有当这几个力同时作用于物体上时,才能求出它们的合力;方法1则不管几个力同时作用,还是作用时间有先后均适用.
例题4:质量为m=3kg的物体放在水平面上,在与水平方向成370角的拉力F=20N作用下匀加速运动,通过位移 S=2m的过程中,物体所受摩擦力大小为6N。(cos370=0.8)求:
WG=0J
WN=0J
Wf =-f S=-12J
W总=WG+WN +Wf +WF=20J
(1)重力对物体做的功
(2)支持力对物体做的功
(3)摩擦力对物体做的功
(4)拉力对物体做的功
(5)合力对物体做的功
W总=F合S=20J
方法一
方法二
WF=FScos370=32J
W总=20J
F
N
G
f
α
【活动四】合力的功
【活动五】变力的功
问题7:恒力做功可以利用公式计算,那么怎样处理变力做功的问题
【微元法】
【例题5】如图所示,一物体在力F的作用下,沿半径为R的圆周绕行一周,若力F的大小保持不变,方向始终沿圆周的切线方向,则力F做了多少功
将物理过程分割成许多个微小的单元,从而达到“化曲为直、化变为恒”的效果,方便分析求解。
将圆周分成很多小段,每一小段小到能将弧线视作直线,力F视作恒力,则在某一微元上,力F所做的功可表示为: , ,·······
因为:
所以:
化曲为直
化变为恒
【图像法】
问题8:如图所示,物块在F=10N水平恒定推力作用下运动了L=10m,力F对物块做的功除了利用公式计算,还有其他方法吗
类比v—t图像的“面积” 可以计算变加速运动的位移。
面积大小表示力F做的功大小(体现了力对位移的累积思想)。
【思考题】如图(a),一质量为m=1kg的滑块(可视为质点)以初速度v0沿水平方向从A滑到B,已知滑块与水平面间的动摩擦因数μ和滑块到A点的距离x的关系如图(b),求摩擦力做的功。
计算面积
(a)
(b)
1.如果物体在某个力的作用下能量发生了变化,这个力一定对物体做了功。功是能量转化的量度
2.做功的两个必要因素:
(1)作用在物体上的力.
(2)物体在这个力的方向上发生一段位移.
3.对公式的理解
W总=W1+W2+……+Wn
作业:练习册
谢 谢
同课章节目录
- 第一章 抛体运动
- 1 认识曲线运动
- 2 运动的合成与分解
- 3 探究平抛运动的特点
- 4 研究平抛运动的规律
- 5 斜抛运动(选学)
- 第二章 匀速圆周运动
- 1 圆周运动
- 2 匀速圆周运动的向心力和向心加速度
- 3 圆周运动的实例分析
- 4 圆周运动与人类文明(选学)
- 第三章 万有引力定律
- 1 天体运动
- 2 万有引力定律
- 3 预言未知星体 计算天体质量
- 4 人造卫星宇宙
- 5 太空探索(选学)
- 第四章 机械能及其守恒定律
- 1 功
- 2 功率
- 3 动能 动能定理
- 4 势能
- 5 机械能守恒定律
- 6 实验:验证机械能守恒定律
- 第五章 经典力学的局限性与相对论初步
- 1 经典力学的成就与局限性
- 2 相对论时空观简介
- 3 宇宙的起源和演化
