沪科版数学七年级下册 9.3 分式方程(第一课时) 课件(共17张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 9.3 分式方程(第一课时) 课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 392.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-22 14:46:13 | ||
图片预览






文档简介
(共18张PPT)
9.3 分式方程
第9章 分 式
导入新课
讲授新课
当堂练习
课堂小结
第1课时 分式方程及其解法
1.理解分式方程的概念;
2.掌握分式方程的解法;(重点)
3.理解分式方程产生增根的原因,掌握分式方程验根的方法.
(难点)
学习目标
1. 什么叫做一元一次方程
只含有一个未知数,未知数的次数都为1,且等式的两边都是整式的方程叫一元一次方程.
导入新课
回顾与思考
3. 解一元一次方程的步骤:
去分母,去括号,移项,合并同类项,未知数系数化为1.
2. 解一元一次方程
解:
思考:若是分母含有未知数的方程改怎样解呢?
七年级甲、乙两班师生前往郊区参加义务植树活动,已知甲班每天比乙班多种10棵树,如果分配给甲、乙两班的植树任务分别是150棵和120棵,问两个班每天各植树多少棵,才能同时完成任务?
分析:
讲授新课
分式方程的概念
一
设甲班每天植树x棵,那么乙班每天植树 棵,
甲班完成任务需要 天,
乙班完成任务需要 天。
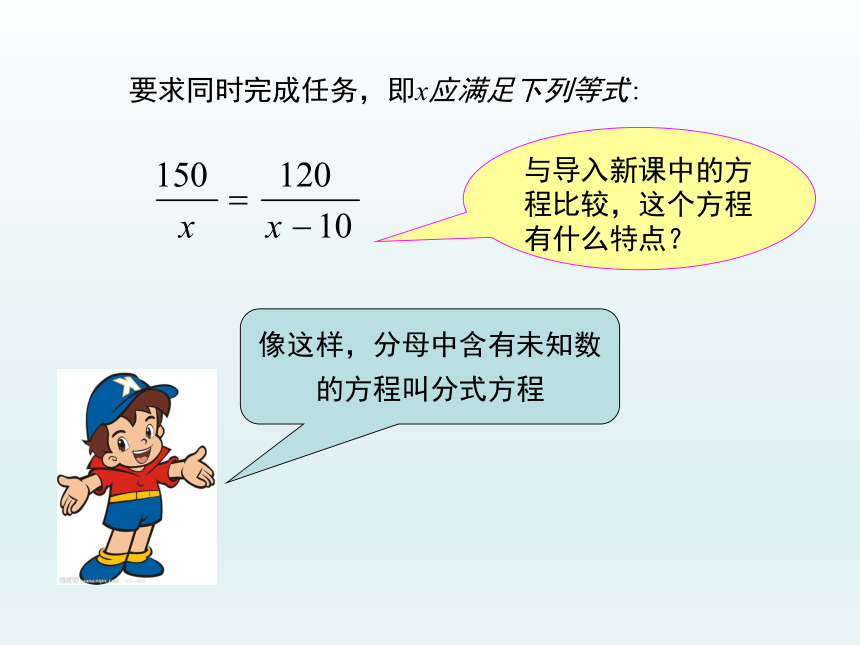
要求同时完成任务,即x应满足下列等式:
与导入新课中的方程比较,这个方程有什么特点?
像这样,分母中含有未知数的方程叫分式方程
例1 下列方程中,哪些是分式方程?哪些整式方程?
解:(2)、(3)是分式方程,(1)、(4)、(5)是整式方程,(6)不是方程.
注意:判断一个方程是不是分式方程,关键是看分母中有没有未知数.(4)中π是一确定的数不是未知数.
典例精析
下面我们一起探究下怎么样来解分式方程:
怎样确定最简公分母?
取各分母的所有因式的最高次幂的积作为公分母.
(类比)
分式方程的解法及增根
二
分式方程的解也叫作分式方程的根.
解得
解:方程两边同乘以 x(x-10) ,得
化归的数学思想:分式方程化为整式方程.
将x=50代入分式方程,左边=3=右边,所以x=50是原分式方程的解.
150(x-10)=120x
150x-1500=120x
150x-120x=1500
30x=1500
x=50
①去分母,等号左右同乘最简公分母
②去括号
③移项
④合并同类项
⑤未知数系数化为一
例2 解方程:
解 :方程两边都乘最简公分母x(x-2),得
解这个一元一次方程,得 x = -3.
把 x=-3 代入原方程的左边和右边,得
因此 x = -3 是原方程的解.
解:两边都乘以最简公分母x-3,得2-x=-1-2(x-3).
解这个方程,得x=3.
检验:把x=3代入原方程,两边分母为0,分式无意义.
因此x=3不是原分式方程的解,从而原方程无解.
在去分母,将分式方程转化为整式方程解的过程中出现使最简公分母(或分母)为零的根是增根.
因此,在解分式方程时必须进行检验.
产生增根的原因:分式方程两边同乘以一个零因式后,所得的根是整式方程的根,而不是分式方程的根.
验根的方法:解分式方程进行检验的关键是看所求得的整式方程的根是否使原分式方程中的分式的分母为零.有时为了简便起见,也可将它代入所乘的整式(即最简公分母),看它的值是否为零.如果为零,即为增根.
总结归纳
解分式方程的一般步骤:
(1)在方程的两边都乘以最简公分母,约去分母化成整式方程;
(2)解这个整式方程;
(3)把方程的根代入原方程,检验是否符合题意.
分
式
方
程
整
式
方
程
x=c
x=c
是否使
最简公
分母的
值为0
两边都乘以最简公分母
解方程
检验
否
原方程
的解
是
增根
1.解方程:
解:方程两边同乘以x-4,
检验:把x=5代入 x-4,得x-4≠0 .
∴x=5是原方程的解.
得x-4+x-5=1,
∴x=5,
当堂练习
(1)
解:方程两边同乘以
检验:把x=2代入(x+2)(x-2) ,得(x+2)(x-2) =0.
∴x=2是增根,从而原方程无解.
2.若关于x的方程 有增根,求m的值.
解:方程两边同乘以x-2,
得2-x+m=2x-4,
合并同类项,得3x=6+m,
∴m=3x-6.
∵该分式方程有增根,
∴x=2,
∴m=0.
(3)把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解,必须舍去;
1.解分式方程的思路:
分式方程
整式方程
去分母
2.解分式方程的一般步骤:
一化二解三检验四写根
(4)写出原方程的根.
(1)方程的两边都乘以最简公分母,约去分母,化成整式方程;
(2)解这个整式方程;
课堂小结
课后作业
课本 第109页
习题9.3 3
9.3 分式方程
第9章 分 式
导入新课
讲授新课
当堂练习
课堂小结
第1课时 分式方程及其解法
1.理解分式方程的概念;
2.掌握分式方程的解法;(重点)
3.理解分式方程产生增根的原因,掌握分式方程验根的方法.
(难点)
学习目标
1. 什么叫做一元一次方程
只含有一个未知数,未知数的次数都为1,且等式的两边都是整式的方程叫一元一次方程.
导入新课
回顾与思考
3. 解一元一次方程的步骤:
去分母,去括号,移项,合并同类项,未知数系数化为1.
2. 解一元一次方程
解:
思考:若是分母含有未知数的方程改怎样解呢?
七年级甲、乙两班师生前往郊区参加义务植树活动,已知甲班每天比乙班多种10棵树,如果分配给甲、乙两班的植树任务分别是150棵和120棵,问两个班每天各植树多少棵,才能同时完成任务?
分析:
讲授新课
分式方程的概念
一
设甲班每天植树x棵,那么乙班每天植树 棵,
甲班完成任务需要 天,
乙班完成任务需要 天。
要求同时完成任务,即x应满足下列等式:
与导入新课中的方程比较,这个方程有什么特点?
像这样,分母中含有未知数的方程叫分式方程
例1 下列方程中,哪些是分式方程?哪些整式方程?
解:(2)、(3)是分式方程,(1)、(4)、(5)是整式方程,(6)不是方程.
注意:判断一个方程是不是分式方程,关键是看分母中有没有未知数.(4)中π是一确定的数不是未知数.
典例精析
下面我们一起探究下怎么样来解分式方程:
怎样确定最简公分母?
取各分母的所有因式的最高次幂的积作为公分母.
(类比)
分式方程的解法及增根
二
分式方程的解也叫作分式方程的根.
解得
解:方程两边同乘以 x(x-10) ,得
化归的数学思想:分式方程化为整式方程.
将x=50代入分式方程,左边=3=右边,所以x=50是原分式方程的解.
150(x-10)=120x
150x-1500=120x
150x-120x=1500
30x=1500
x=50
①去分母,等号左右同乘最简公分母
②去括号
③移项
④合并同类项
⑤未知数系数化为一
例2 解方程:
解 :方程两边都乘最简公分母x(x-2),得
解这个一元一次方程,得 x = -3.
把 x=-3 代入原方程的左边和右边,得
因此 x = -3 是原方程的解.
解:两边都乘以最简公分母x-3,得2-x=-1-2(x-3).
解这个方程,得x=3.
检验:把x=3代入原方程,两边分母为0,分式无意义.
因此x=3不是原分式方程的解,从而原方程无解.
在去分母,将分式方程转化为整式方程解的过程中出现使最简公分母(或分母)为零的根是增根.
因此,在解分式方程时必须进行检验.
产生增根的原因:分式方程两边同乘以一个零因式后,所得的根是整式方程的根,而不是分式方程的根.
验根的方法:解分式方程进行检验的关键是看所求得的整式方程的根是否使原分式方程中的分式的分母为零.有时为了简便起见,也可将它代入所乘的整式(即最简公分母),看它的值是否为零.如果为零,即为增根.
总结归纳
解分式方程的一般步骤:
(1)在方程的两边都乘以最简公分母,约去分母化成整式方程;
(2)解这个整式方程;
(3)把方程的根代入原方程,检验是否符合题意.
分
式
方
程
整
式
方
程
x=c
x=c
是否使
最简公
分母的
值为0
两边都乘以最简公分母
解方程
检验
否
原方程
的解
是
增根
1.解方程:
解:方程两边同乘以x-4,
检验:把x=5代入 x-4,得x-4≠0 .
∴x=5是原方程的解.
得x-4+x-5=1,
∴x=5,
当堂练习
(1)
解:方程两边同乘以
检验:把x=2代入(x+2)(x-2) ,得(x+2)(x-2) =0.
∴x=2是增根,从而原方程无解.
2.若关于x的方程 有增根,求m的值.
解:方程两边同乘以x-2,
得2-x+m=2x-4,
合并同类项,得3x=6+m,
∴m=3x-6.
∵该分式方程有增根,
∴x=2,
∴m=0.
(3)把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解,必须舍去;
1.解分式方程的思路:
分式方程
整式方程
去分母
2.解分式方程的一般步骤:
一化二解三检验四写根
(4)写出原方程的根.
(1)方程的两边都乘以最简公分母,约去分母,化成整式方程;
(2)解这个整式方程;
课堂小结
课后作业
课本 第109页
习题9.3 3
