5.2 导数的运算 课件(73张PPT)
文档属性
| 名称 | 5.2 导数的运算 课件(73张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 15.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-21 22:59:19 | ||
图片预览




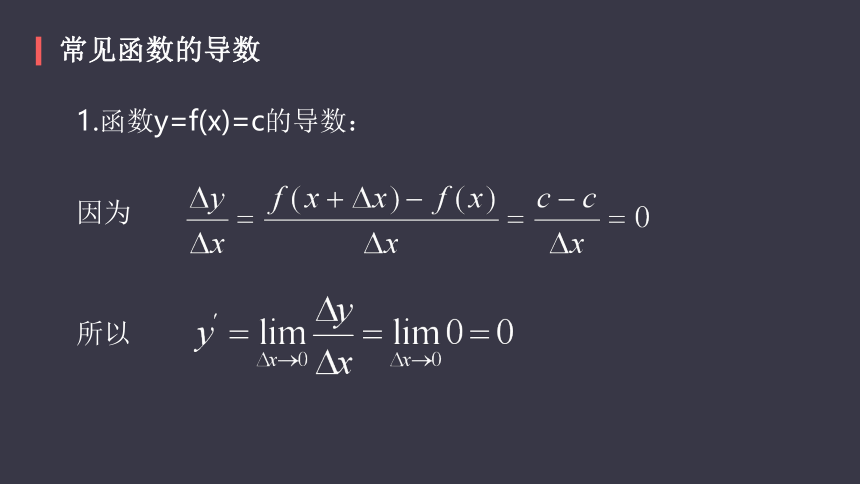





文档简介
(共73张PPT)
导数的运算
教学目标
根据导数定义求基本函数的导数;
掌握基本初等函数的导数公式;
会运用导数的四则运算法则及简单复合函数的复合过程。
教学重点
教学难点
理解并熟练记忆基本初等函数的导数公式表;掌握函数积与商的导数公式;掌握复合函数的求导方法。
我们知道,导数的几何意义是曲线在某点处的切线的斜率,物理意义是运动物体在某一时刻的瞬时速度。那么,对于函数y=f(x),如何求它的导数呢?
引入
(3)求极限
常见函数的导数
1.函数y=f(x)=c的导数:
因为
所以
常见函数的导数
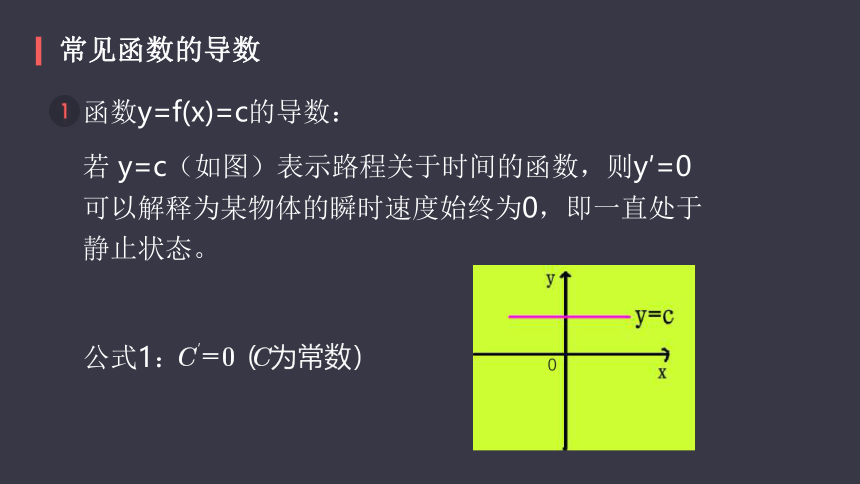
函数y=f(x)=c的导数:
若 y=c(如图)表示路程关于时间的函数,则y′=0可以解释为某物体的瞬时速度始终为0,即一直处于静止状态。
公式1:
常见函数的导数
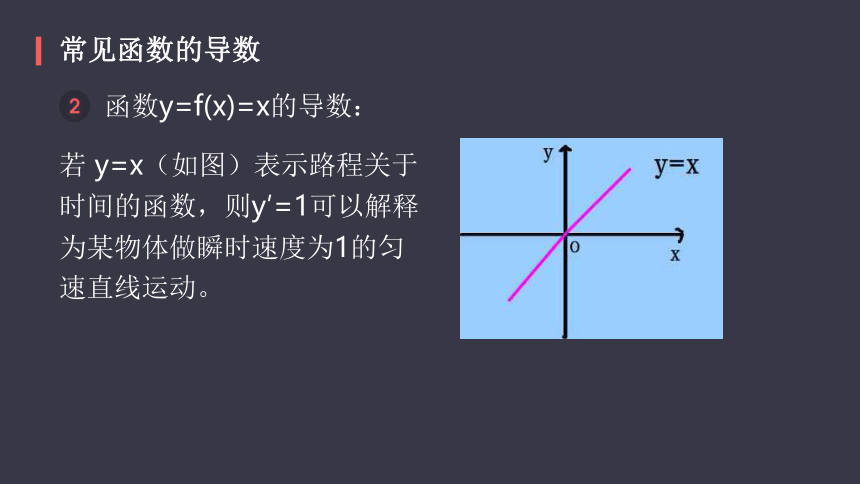
函数y=f(x)=x的导数:
因为
所以
常见函数的导数
函数y=f(x)=x的导数:
若 y=x(如图)表示路程关于时间的函数,则y′=1可以解释为某物体做瞬时速度为1的匀速直线运动。
常见函数的导数
函数y=f(x)=x2的导数:
因为
所以
常见函数的导数
函数y=f(x)=x2的导数
若 表示路程关于时间的函数,则 可以解释为某物体做变速速度,它在时刻x的瞬时速度为2x。
常见函数的导数
函数y=f(x)=x3的导数
因为
所以
常见函数的导数
函数y=f(x)= 的导数
观察导函数,你能否把它和原函数进行对应?
表示函数 的图象(图5.24)上点(x,y)处切线的斜率为 ,这说明随着x的变化,切线的斜率也在变化,且恒为非负数.
常见函数的导数
因为
所以
常见函数的导数
思考:以上2~5出现的函数有什么共同点?
比较它们本身的形式和导函数的形式,你能否发现更加普适的规律?
因为
所以
常见函数的导数
注意:根据我们所掌握的知识,只能就n是整数的情况加以证明。这个公式称为幂函数的导数公式。事实上n可以是任意实数。
公式2:
前面我们根据导数的定义求出了一些常用函数的导数,一般地,有下面的基本初等函数的导数公式表(表5.2-1),这些公式可以直接使用.
常见函数的导数
基本初等函数的导数公式
例题
例1:求下列函数的导数:
(1)
解:
(2)
例题
例2:假设某地在20年间的年均通货膨胀率为5%,物价p(单位:元)与时间(单位:年)有如下函数关系
,
其中 为t=0时的物价、假定某种商品的 =1,那么在第10个年头,这种商品的价格上涨的速度大约是多少(精确到0.01元/年)
解:根据基本初等函数的导数公式表,有
所以
所以,在第10个年头,这种商品的价格约以0.08元/年的速度上涨.
练习1
求下列函数的导数:
解:
练习2
求下列函数在给定点的导数:
解:(1)405
(2)
(3)1
(4)1
练习3
解:
y'=-sinx
练习4
解:
和(或差)的导数
设 ,g(x)=x,计算[f(x)+g(x)]'与[f(x)-g(x)],它们与f(x)和g'(x)有什么关系?再取几组函数试试,上述关系仍然成立吗?由此你能想到什么
若f(x),g(x)在x处可导,则
[f(x)+g(x)]'=f'(x)+g'(x)
例
所以
而
[f(x)+g(x)]'=f'(x)+g'(x)
[f(x)-g(x)]'=f'(x)-g'(x)
同样的,对于上述函数,
和(或差)的导数
若f(x),g(x)在x处可导,则
例题
例3:求下列函数的导数
解:
积的导数
设 ,g(x)=x,计算[f(x)g(x)]与f(x)g'(x),它们是否相等?f(x)与g(x)商的导数是否等于它们导数的商呢?
通过计算可知, , f'(x)g'(x)=2x·1=2x,
因此[f(x)g(x)]'≠f'(x)g'(x) .同样的,
积(或商)的导数
解:由导数的基本公式得:
积(或商)的导数
积(或商)的导数
该公式同时也可以视为导数积公式的推论。
例题
例:求下列函数的导数:
解:
(1)
(2)
例题
例:日常生活中的饮用水通常是经过净化的。随着水的纯净度的提高,所需净化费用不断增加。已知将1t水净化到纯净度为x%时所需费用(单位:元)为
求净化到下列纯净度时,所需净化费用的瞬时变化率:
(1)90%;(2)98%
解:
净化费用的瞬时变化率就是净化费用函数的导数
例题
(1)因为 ,所以,净化到纯净度为
(2)因为 ,所以,净化到纯净度为
90%时,净化费用的瞬时变化率是52.84元/吨.
98%时,净化费用的时变化率是1321元/吨.
练习
运用基本初等函数的导数公式与导数运算法则,重新求解5.1节例2.你是否感觉到运算法则给解题带来的方便简捷?
解:
y'=2x-7
x=2,y'=-3
x=6,y'=5
练习
求下列函数的导数
解:
解:
练习
练习
解:
当x=1时,y'=-1
所以切线方程为y-4=-(x-1)
即y=-x+5
掌握导数四则运算的公式和方法
导函数的直接计算
简单复合函数的导数
思考:如何求函数y=㏑(2x-1)的函数呢?
我们无法用现有的方法求函数y=㏑(2x-1)的导数。下面,我们先分析这个函数的结构特点。
简单复合函数的导数
一般地,对于两个函数y=f(u)和u=g(x),如果通过变量u,y可以表示成x的函数,那么称这个函数为函数y=f(u)和u=g(x)的复合函数。记做y=f(g(x))。
简单复合函数的导数
如何求复合函数的导数呢?我们先来研究y=sin2x的导数。
一个合理的猜想是,函数y=sin2x的导数一定与函数y=sinu,u=2x的导数有关。下面我们就来研究这种关系。
简单复合函数的导数
复合函数y=f(g(x))的导数和函数y=f(u),u=g(x)的导数间的关系为
即y对x的导数等于y对u的导数与u对x的导数的乘积。
例题
求下列函数的导数:
解:
例题
解:
例题
解:(3)函数y=ln(2x-1)可以看作函数y=lnu和u=2x-1的复合函数。根据复合函数的求导法则,有
例题
某个弹簧振子在振动过程中的位移y(单位:mm)关于时间t(单位:s)的函数满足关系式 。求函数y在t=3s时的导数,并解释它的实际意义.
解:
它表示当t=3s时,弹簧振子振动的瞬时速度为0mm/s
练习
求下列函数的导数:
解:
练习
解:
练习
解:
练习
解:
练习
解:
练习
解:
练习
求下列函数在给定点的导数
解:
练习
解:
练习
解:
掌握复合函数的导数求法
复合函数的导数
习题
求下列函数的导数
解:
习题
求下列函数的导数:
解:
习题
解:
习题
解:
习题
解:
习题
求下列函数的导数:
解:
习题
解:
习题
解:
习题
解:
小结
分层
选择中间变量,写出构成它的内、外层函数
分别求导
分别求各层函数对相应变量的导数
相乘
把上述求导的结果相乘
变量回代
把中间变量回代
求复合函数的导数的步骤
习题
求下列函数的导数:
解:
习题
解:
习题
解:
习题
解:
习题
解:
习题
解:
总结
导数的运算
常见函数的导数计算
导数的四则运算
复合函数的导数计算
导数的运算
教学目标
根据导数定义求基本函数的导数;
掌握基本初等函数的导数公式;
会运用导数的四则运算法则及简单复合函数的复合过程。
教学重点
教学难点
理解并熟练记忆基本初等函数的导数公式表;掌握函数积与商的导数公式;掌握复合函数的求导方法。
我们知道,导数的几何意义是曲线在某点处的切线的斜率,物理意义是运动物体在某一时刻的瞬时速度。那么,对于函数y=f(x),如何求它的导数呢?
引入
(3)求极限
常见函数的导数
1.函数y=f(x)=c的导数:
因为
所以
常见函数的导数
函数y=f(x)=c的导数:
若 y=c(如图)表示路程关于时间的函数,则y′=0可以解释为某物体的瞬时速度始终为0,即一直处于静止状态。
公式1:
常见函数的导数
函数y=f(x)=x的导数:
因为
所以
常见函数的导数
函数y=f(x)=x的导数:
若 y=x(如图)表示路程关于时间的函数,则y′=1可以解释为某物体做瞬时速度为1的匀速直线运动。
常见函数的导数
函数y=f(x)=x2的导数:
因为
所以
常见函数的导数
函数y=f(x)=x2的导数
若 表示路程关于时间的函数,则 可以解释为某物体做变速速度,它在时刻x的瞬时速度为2x。
常见函数的导数
函数y=f(x)=x3的导数
因为
所以
常见函数的导数
函数y=f(x)= 的导数
观察导函数,你能否把它和原函数进行对应?
表示函数 的图象(图5.24)上点(x,y)处切线的斜率为 ,这说明随着x的变化,切线的斜率也在变化,且恒为非负数.
常见函数的导数
因为
所以
常见函数的导数
思考:以上2~5出现的函数有什么共同点?
比较它们本身的形式和导函数的形式,你能否发现更加普适的规律?
因为
所以
常见函数的导数
注意:根据我们所掌握的知识,只能就n是整数的情况加以证明。这个公式称为幂函数的导数公式。事实上n可以是任意实数。
公式2:
前面我们根据导数的定义求出了一些常用函数的导数,一般地,有下面的基本初等函数的导数公式表(表5.2-1),这些公式可以直接使用.
常见函数的导数
基本初等函数的导数公式
例题
例1:求下列函数的导数:
(1)
解:
(2)
例题
例2:假设某地在20年间的年均通货膨胀率为5%,物价p(单位:元)与时间(单位:年)有如下函数关系
,
其中 为t=0时的物价、假定某种商品的 =1,那么在第10个年头,这种商品的价格上涨的速度大约是多少(精确到0.01元/年)
解:根据基本初等函数的导数公式表,有
所以
所以,在第10个年头,这种商品的价格约以0.08元/年的速度上涨.
练习1
求下列函数的导数:
解:
练习2
求下列函数在给定点的导数:
解:(1)405
(2)
(3)1
(4)1
练习3
解:
y'=-sinx
练习4
解:
和(或差)的导数
设 ,g(x)=x,计算[f(x)+g(x)]'与[f(x)-g(x)],它们与f(x)和g'(x)有什么关系?再取几组函数试试,上述关系仍然成立吗?由此你能想到什么
若f(x),g(x)在x处可导,则
[f(x)+g(x)]'=f'(x)+g'(x)
例
所以
而
[f(x)+g(x)]'=f'(x)+g'(x)
[f(x)-g(x)]'=f'(x)-g'(x)
同样的,对于上述函数,
和(或差)的导数
若f(x),g(x)在x处可导,则
例题
例3:求下列函数的导数
解:
积的导数
设 ,g(x)=x,计算[f(x)g(x)]与f(x)g'(x),它们是否相等?f(x)与g(x)商的导数是否等于它们导数的商呢?
通过计算可知, , f'(x)g'(x)=2x·1=2x,
因此[f(x)g(x)]'≠f'(x)g'(x) .同样的,
积(或商)的导数
解:由导数的基本公式得:
积(或商)的导数
积(或商)的导数
该公式同时也可以视为导数积公式的推论。
例题
例:求下列函数的导数:
解:
(1)
(2)
例题
例:日常生活中的饮用水通常是经过净化的。随着水的纯净度的提高,所需净化费用不断增加。已知将1t水净化到纯净度为x%时所需费用(单位:元)为
求净化到下列纯净度时,所需净化费用的瞬时变化率:
(1)90%;(2)98%
解:
净化费用的瞬时变化率就是净化费用函数的导数
例题
(1)因为 ,所以,净化到纯净度为
(2)因为 ,所以,净化到纯净度为
90%时,净化费用的瞬时变化率是52.84元/吨.
98%时,净化费用的时变化率是1321元/吨.
练习
运用基本初等函数的导数公式与导数运算法则,重新求解5.1节例2.你是否感觉到运算法则给解题带来的方便简捷?
解:
y'=2x-7
x=2,y'=-3
x=6,y'=5
练习
求下列函数的导数
解:
解:
练习
练习
解:
当x=1时,y'=-1
所以切线方程为y-4=-(x-1)
即y=-x+5
掌握导数四则运算的公式和方法
导函数的直接计算
简单复合函数的导数
思考:如何求函数y=㏑(2x-1)的函数呢?
我们无法用现有的方法求函数y=㏑(2x-1)的导数。下面,我们先分析这个函数的结构特点。
简单复合函数的导数
一般地,对于两个函数y=f(u)和u=g(x),如果通过变量u,y可以表示成x的函数,那么称这个函数为函数y=f(u)和u=g(x)的复合函数。记做y=f(g(x))。
简单复合函数的导数
如何求复合函数的导数呢?我们先来研究y=sin2x的导数。
一个合理的猜想是,函数y=sin2x的导数一定与函数y=sinu,u=2x的导数有关。下面我们就来研究这种关系。
简单复合函数的导数
复合函数y=f(g(x))的导数和函数y=f(u),u=g(x)的导数间的关系为
即y对x的导数等于y对u的导数与u对x的导数的乘积。
例题
求下列函数的导数:
解:
例题
解:
例题
解:(3)函数y=ln(2x-1)可以看作函数y=lnu和u=2x-1的复合函数。根据复合函数的求导法则,有
例题
某个弹簧振子在振动过程中的位移y(单位:mm)关于时间t(单位:s)的函数满足关系式 。求函数y在t=3s时的导数,并解释它的实际意义.
解:
它表示当t=3s时,弹簧振子振动的瞬时速度为0mm/s
练习
求下列函数的导数:
解:
练习
解:
练习
解:
练习
解:
练习
解:
练习
解:
练习
求下列函数在给定点的导数
解:
练习
解:
练习
解:
掌握复合函数的导数求法
复合函数的导数
习题
求下列函数的导数
解:
习题
求下列函数的导数:
解:
习题
解:
习题
解:
习题
解:
习题
求下列函数的导数:
解:
习题
解:
习题
解:
习题
解:
小结
分层
选择中间变量,写出构成它的内、外层函数
分别求导
分别求各层函数对相应变量的导数
相乘
把上述求导的结果相乘
变量回代
把中间变量回代
求复合函数的导数的步骤
习题
求下列函数的导数:
解:
习题
解:
习题
解:
习题
解:
习题
解:
习题
解:
总结
导数的运算
常见函数的导数计算
导数的四则运算
复合函数的导数计算
