5.3 导数在研究函数中的应用 课件(85张PPT)
文档属性
| 名称 | 5.3 导数在研究函数中的应用 课件(85张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 15.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-21 23:01:13 | ||
图片预览










文档简介
(共85张PPT)
导数在研究函数中的应用
教学目标
从函数的几何图形上观察、探究最大(小)值与极值、两个端点处的函数值之间的关系,总结出一般规律,并用来求一些简单(连续)函数的最大(小)值。
应用导数探索函数的单调性,解决实际问题;
理解函数的极大值、极小值、极值点的意义,掌握函数极值的判别方法;
教学重点
利用导数研究函数的单调性;会求不超过三次的多项式函数的单调区间。
教学难点
函数在某点能取到极值的必要条件和充分条件。
函数的单调性与导数
函数的单调性与导数
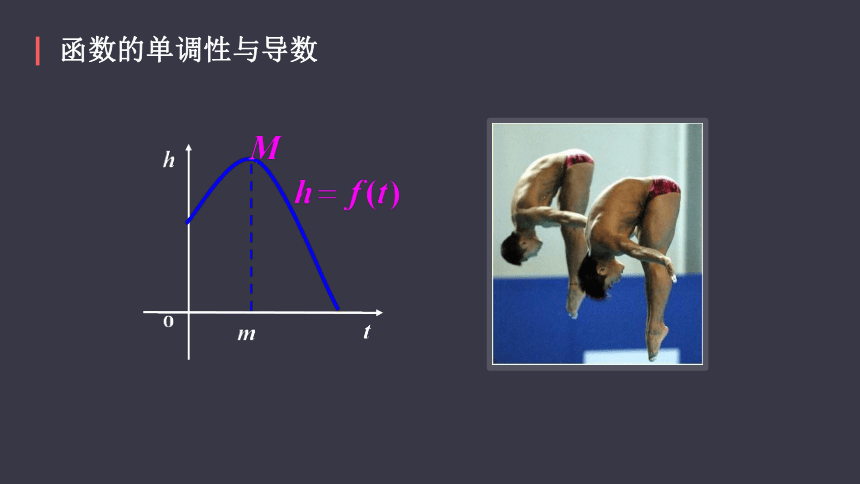
左边表示高台跳水运动员的高度h随时间t变化的函数的图像。
运动员从起跳到最高点,以及从最高点到入水这两段时间内,随着时间的变化,运动员离水面的高度发生什么变化?
函数的单调性与导数
这种情况是否具有一般性呢
函数的单调性与导数
函数的单调性与导数
如果在某个区间内恒有f ’(x)=0,那么函数f(x)有什么特性?
在该区间内函数值不变,图像为水平直线。
函数的单调性与导数
x
f '(x)
f (x)
+
单调递增
-1
0
(-1,2)
-
单调递减
2
0
+
单调递增
函数的单调性与导数
第1步,确定函数的定义域;
函数的单调性与导数
函数的单调性与导数
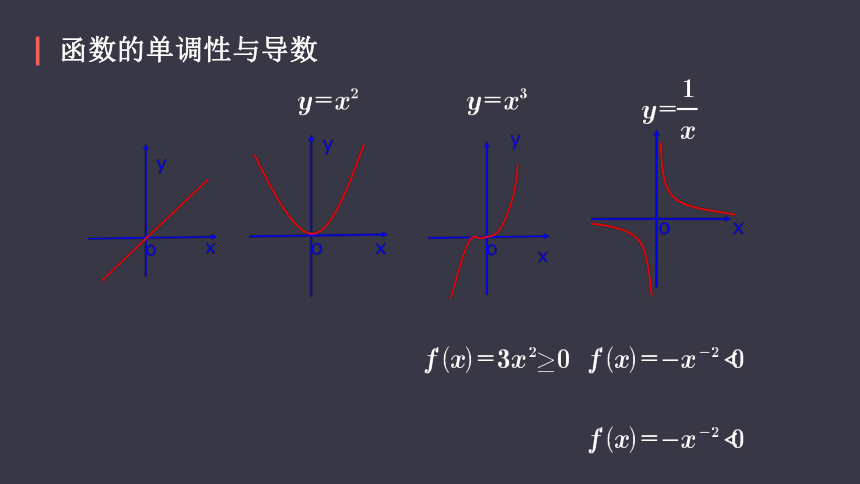
一般地,如果一个函数在某一范围内导数的绝对值较大,那么函数在这个范围内变化得较快,这时函数的图象就比较“陡峭”(向上或向下);反之,函数在这个范围内变化得较慢,函数的图象就比较“平缓”
x
f '(x)
f (x)
单调递减
-1
0
(-1,1)
单调递增
0
单调递减
-
-2
+
1
2
-
x
f '(x)
f (x)
单调递增
0
单调递减
0
单调递增
1
+
-
-1
+
理解导数正负和单调性的关系,通过导数判断函数的单调性,并写出单调区间
利用导数判断函数的单调性
(-3,1)
D
函数的极值与最大(小)值
函数的极值与最大(小)值
观察上图,可以发现t=a时,高台跳水运动员距水面的高度最大,那么函数在此点的导数是多少?此点附近的图像有什么特点?相应的,导数的符号有什么变化规律?
函数的极值与最大(小)值
函数的极值与最大(小)值
函数的极值与最大(小)值
函数的极值与最大(小)值
x
f '(x)
f (x)
+
单调递增
-2
0
(-2,2)
-
单调递减
2
0
+
单调递增
1.同一函数,极大值一定大于极小值吗?
函数的极值与最大(小)值
函数的极值与最大(小)值
掌握导数极值的判断方法
函数的极值
D
D
函数的极值与最大(小)值
极值反映的是函数在某一点附近的局部性质,而不是函数在整个定义域的性质。但是,在解决实际问题或在研究函数性质时,往往更关心函数在某个区间上哪个值最大,哪个值最小?
函数的极值与最大(小)值
观察一个定义在区间[a,b]上的函数y=f(x)的图象。
在上图中,观察[a,b]上的函数y=f(x)的图像,它们在[a,b]上是否有最大值﹑最小值?如果有,分别是多少?
函数的极值与最大(小)值
函数的极值与最大(小)值
函数的极值与最大(小)值
函数的极值与最大(小)值
x
s '(x)
s (x)
单调递增
0
单调递减
-
1
0
+
函数的极值与最大(小)值
x
f '(x)
f (x)
单调递增
0
单调递减
-
1
0
+
x
f '(x)
f (x)
+
单调递增
-2
0
+
单调递减
函数的极值与最大(小)值
函数的极值与最大(小)值
A
恒成立问题的转化
常见恒成立问题
拓展:恒成立与存在性问题
拓展:恒成立与存在性问题
(7,+∞)
拓展:函数的零点问题
拓展:恒成立与存在性问题
提示:关键是把题目中的不等式转化为求最值问题
拓展:恒成立与存在性问题
常见存在性问题
拓展:恒成立与存在性问题
拓展:恒成立与存在性问题
拓展:恒成立与存在性问题
B
拓展:构造新函数解不等式
拓展:构造新函数解不等式
A
拓展:构造新函数解不等式
D
拓展:构造新函数解不等式
D
拓展:构造新函数解不等式
B
拓展:函数的零点问题
零点问题的转换
(1)f(x)的零点 f(x)=0的根 ______与_______的交点;
(2)F(x)=f(x)-a的零点 f(x)-a=0的根 ______与_______的交点;
(3)F(x)=f(x)-g(x)的零点 f(x)-g(x)=0的根 ______与_______的交点。
f(x)
x轴
f(x)
y=a
f(x)
g(x)
拓展:函数的零点问题
D
拓展:函数的零点问题
拓展:函数的零点问题
总结
导数在研究函数中的应用
1.利用导数判断函数的单调性
2.利用导数求函数的极值
3.参考极其求函数的最值
4*.导数的恒成立与存在性问题
5*.构造新函数求导技巧
6*.函数的零点问题
导数在研究函数中的应用
教学目标
从函数的几何图形上观察、探究最大(小)值与极值、两个端点处的函数值之间的关系,总结出一般规律,并用来求一些简单(连续)函数的最大(小)值。
应用导数探索函数的单调性,解决实际问题;
理解函数的极大值、极小值、极值点的意义,掌握函数极值的判别方法;
教学重点
利用导数研究函数的单调性;会求不超过三次的多项式函数的单调区间。
教学难点
函数在某点能取到极值的必要条件和充分条件。
函数的单调性与导数
函数的单调性与导数
左边表示高台跳水运动员的高度h随时间t变化的函数的图像。
运动员从起跳到最高点,以及从最高点到入水这两段时间内,随着时间的变化,运动员离水面的高度发生什么变化?
函数的单调性与导数
这种情况是否具有一般性呢
函数的单调性与导数
函数的单调性与导数
如果在某个区间内恒有f ’(x)=0,那么函数f(x)有什么特性?
在该区间内函数值不变,图像为水平直线。
函数的单调性与导数
x
f '(x)
f (x)
+
单调递增
-1
0
(-1,2)
-
单调递减
2
0
+
单调递增
函数的单调性与导数
第1步,确定函数的定义域;
函数的单调性与导数
函数的单调性与导数
一般地,如果一个函数在某一范围内导数的绝对值较大,那么函数在这个范围内变化得较快,这时函数的图象就比较“陡峭”(向上或向下);反之,函数在这个范围内变化得较慢,函数的图象就比较“平缓”
x
f '(x)
f (x)
单调递减
-1
0
(-1,1)
单调递增
0
单调递减
-
-2
+
1
2
-
x
f '(x)
f (x)
单调递增
0
单调递减
0
单调递增
1
+
-
-1
+
理解导数正负和单调性的关系,通过导数判断函数的单调性,并写出单调区间
利用导数判断函数的单调性
(-3,1)
D
函数的极值与最大(小)值
函数的极值与最大(小)值
观察上图,可以发现t=a时,高台跳水运动员距水面的高度最大,那么函数在此点的导数是多少?此点附近的图像有什么特点?相应的,导数的符号有什么变化规律?
函数的极值与最大(小)值
函数的极值与最大(小)值
函数的极值与最大(小)值
函数的极值与最大(小)值
x
f '(x)
f (x)
+
单调递增
-2
0
(-2,2)
-
单调递减
2
0
+
单调递增
1.同一函数,极大值一定大于极小值吗?
函数的极值与最大(小)值
函数的极值与最大(小)值
掌握导数极值的判断方法
函数的极值
D
D
函数的极值与最大(小)值
极值反映的是函数在某一点附近的局部性质,而不是函数在整个定义域的性质。但是,在解决实际问题或在研究函数性质时,往往更关心函数在某个区间上哪个值最大,哪个值最小?
函数的极值与最大(小)值
观察一个定义在区间[a,b]上的函数y=f(x)的图象。
在上图中,观察[a,b]上的函数y=f(x)的图像,它们在[a,b]上是否有最大值﹑最小值?如果有,分别是多少?
函数的极值与最大(小)值
函数的极值与最大(小)值
函数的极值与最大(小)值
函数的极值与最大(小)值
x
s '(x)
s (x)
单调递增
0
单调递减
-
1
0
+
函数的极值与最大(小)值
x
f '(x)
f (x)
单调递增
0
单调递减
-
1
0
+
x
f '(x)
f (x)
+
单调递增
-2
0
+
单调递减
函数的极值与最大(小)值
函数的极值与最大(小)值
A
恒成立问题的转化
常见恒成立问题
拓展:恒成立与存在性问题
拓展:恒成立与存在性问题
(7,+∞)
拓展:函数的零点问题
拓展:恒成立与存在性问题
提示:关键是把题目中的不等式转化为求最值问题
拓展:恒成立与存在性问题
常见存在性问题
拓展:恒成立与存在性问题
拓展:恒成立与存在性问题
拓展:恒成立与存在性问题
B
拓展:构造新函数解不等式
拓展:构造新函数解不等式
A
拓展:构造新函数解不等式
D
拓展:构造新函数解不等式
D
拓展:构造新函数解不等式
B
拓展:函数的零点问题
零点问题的转换
(1)f(x)的零点 f(x)=0的根 ______与_______的交点;
(2)F(x)=f(x)-a的零点 f(x)-a=0的根 ______与_______的交点;
(3)F(x)=f(x)-g(x)的零点 f(x)-g(x)=0的根 ______与_______的交点。
f(x)
x轴
f(x)
y=a
f(x)
g(x)
拓展:函数的零点问题
D
拓展:函数的零点问题
拓展:函数的零点问题
总结
导数在研究函数中的应用
1.利用导数判断函数的单调性
2.利用导数求函数的极值
3.参考极其求函数的最值
4*.导数的恒成立与存在性问题
5*.构造新函数求导技巧
6*.函数的零点问题
