2.1 直线的倾斜角与斜率 课件(49张PPT)
文档属性
| 名称 | 2.1 直线的倾斜角与斜率 课件(49张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 11.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-21 00:00:00 | ||
图片预览







文档简介
(共49张PPT)
直线的倾斜角与斜率
理解直线倾斜角、斜率的概念
教学目标
理解并掌握直线斜率的求法
能够根据两条直线的斜率相等判断两条直线平行
能够根据两条直线的斜率之积等于-1,判断两条直线垂直
教学重点
直线斜率的求法
斜率判断两条直线的位置关系
教学难点
斜率判断两条直线的位置关系
问题1:如何确定一条直线在直角坐标系的位置呢?
两点或一点和方向
问题2:如果已知一点还需附加什么条件,才能确定直线?
一点和方向
问题3:如何表示方向?
用角
倾斜角与斜率
直线的倾斜角的定义
当直线l与x轴相交时,我们取x轴作为基准,x轴
正向与直线l向上方向之间所成的角α叫做直线的倾斜角。
α
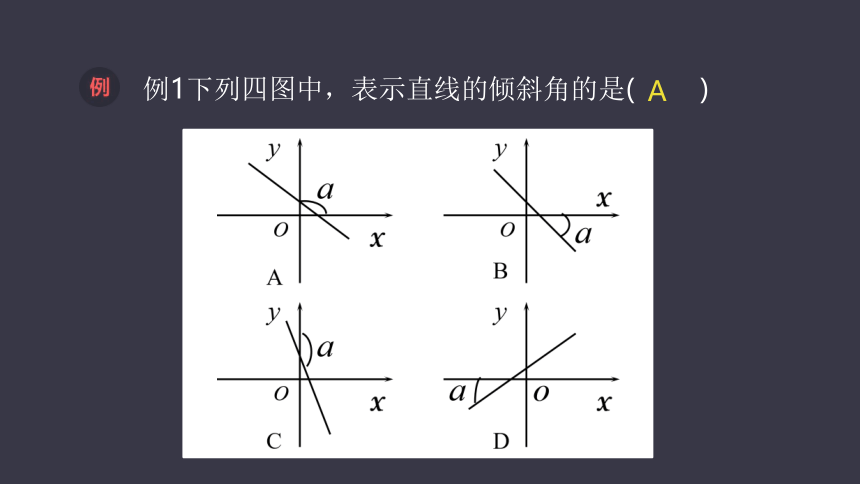
例1下列四图中,表示直线的倾斜角的是( )
A
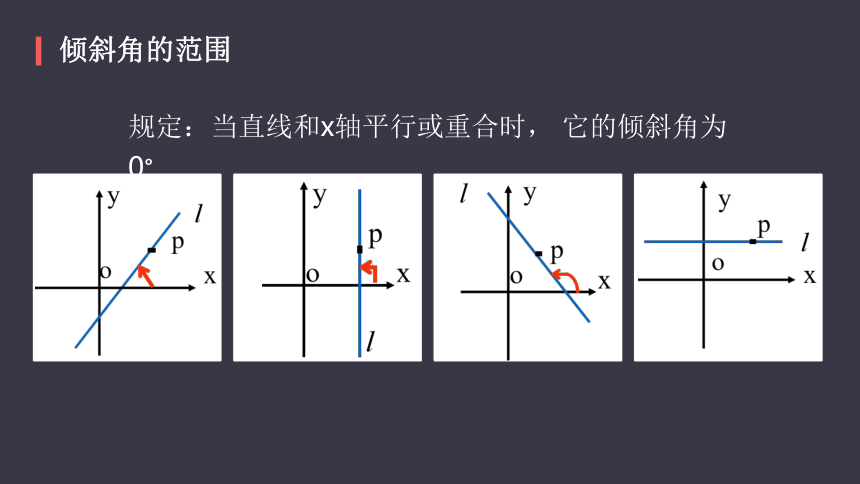
倾斜角的范围
规定:当直线和x轴平行或重合时, 它的倾斜角为0°
直线的斜率
定义:我们把一条直线的倾斜角α的正切值叫做这条直线的斜率.
用小写字母 k 表示,即:
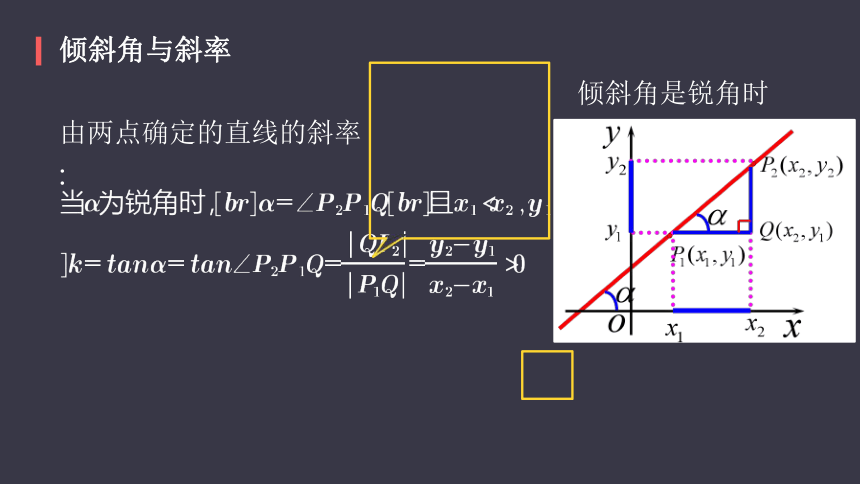
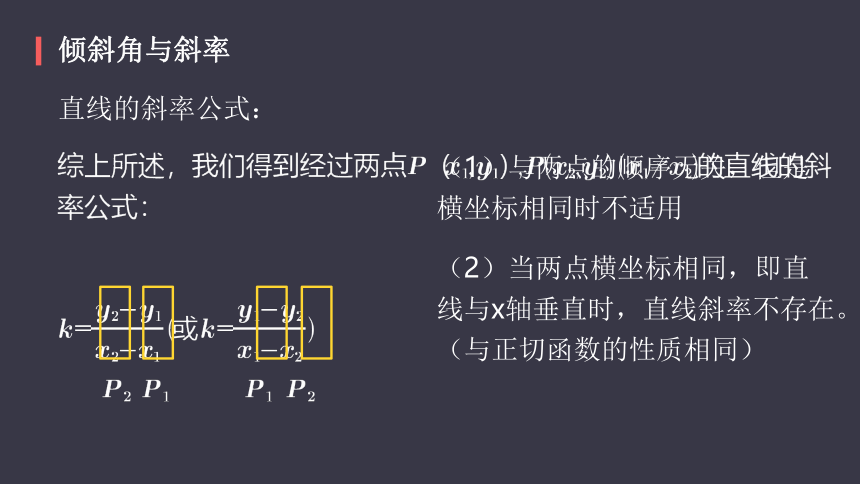
由两点确定的直线的斜率:
倾斜角与斜率
倾斜角是锐角时
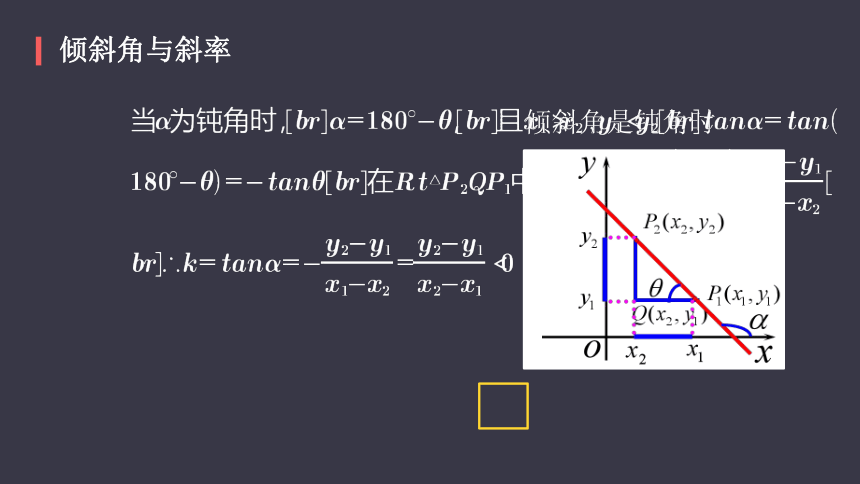
倾斜角与斜率
倾斜角是钝角时
直线的斜率公式:
倾斜角与斜率
(1)与两点的顺序无关,但是横坐标相同时不适用
(2)当两点横坐标相同,即直线与x轴垂直时,直线斜率不存在。(与正切函数的性质相同)
2.如图2.1-6, 已知A(3, 2), B(-4, 1), C(0,-1),求直线AB,BC, CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
3.(1)若直线的倾斜角为60°,则直线的斜率为( )
(2)已知过A(3,1),B(m,-2)的直线的斜率为1,则m的值为____.
A
0
4.如果三点A(2,1),B(-2,m),C(6,8)在同一条直线上,求实数m的值.
1.已知下列直线的倾斜角,求直线的斜率:
3.求经过下列两点的直线的斜率,并判断其倾斜角是锐角还是钝角 (1) C(18, 8),D(4, -4); (2) P(0, 0), Q(-1, 3).
4.已知a, b, c是两两不等的实数,求经过下列两点的直线的倾斜角:
(1) A(a, c), B(b,c) (2) C(a, b), D(a, c) (3) P(b, b+c), Q(a. c+a).
5.经过A(0, 2),B(-1, 0)两点的直线的方向向量为(1, k),求k的值.
理解并掌握倾斜角的概念
理解并掌握倾斜角和斜率的关系
能跟据两点坐标求出直线斜率
直线的斜率和倾斜角
两条直线平行判定
斜率存在时两直线平行.
两条直线平行的判定
此结论常用来证明三点共线
注意:上面的等价是在两直线斜率存在的前提下才
成立的,缺少这个前提,结论并不成立.
特殊情况下的两直线平行:两直线的斜率都不存在时,互相平行.
5 .已知A(2, 3), B(-4, 0),P(-3,1),Q(-1, 2),试判断直线AB与PQ的位置关系,并证明你的结论.
6.已知四边形 ABCD的四个顶点分别为A(O,0), B(2,1-1), C(4, 2), D(2, 3),试判断四边形ABCD的形状,并给出证明
理解并掌握两条直线平行的条件
能够熟练掌握直线平行条件的应用
直线的平行关系2
两条直线垂直的判定
斜率存在时两直线垂直
两条直线垂直的判定
注意:上面的等价是在两直线斜率存在的前提下才成立的,
缺少这个前提,结论并不成立.
特殊情况下的两直线垂直.
当两条直线中有一条直线斜率不存在,另一条
直线的斜率为0时,两直线垂直。
7.已知A(-6, 0),B(3, 6),P(0, 3), Q(6, -6),试判断直线AB与PQ的位置关系.
8.已知A(5, -1),B(1, 1), C(2, 3)三点,试判断△ABC的形状.
9.已知长方形ABCD的三个顶点的坐标分别为A(0,1),B(1,0),C(3,2),求第四个顶点D的坐标.
2.试确定m的值,使过A(m, 1),B(-1,m)两点的直线与过P(1,2),Q(-5, 0)两点的直线:
(1)平行; (2)垂直.
理解并掌握两条直线垂直的条件
能够熟练掌握直线垂直条件的应用
直线的垂直关系2
1.已知直线斜率的绝对值等于1,求直线的倾斜角.
直线斜率的绝对值等于1,可得直线的倾斜角为: 45° 或135°
2.已知四边形ABCD的四个顶点是A(2, 3), B(1, -1),C(-1,一2),D(一-2, 2), 求四边形ABCD的四条边所在直线的斜率.
3. m为何值时,(1)经过A(-m, 6),B(1, 3m)两点的直线的斜率是12
(2)经过A(m,2), B(-m,-2m-1)两点的直线的倾斜角是60°
4. 已知A(1, 2), B(-1. 0), C(3, 4) 三点,这三点是否在同一条直线上 为什么
8. 经过点P(0,-1)作直线1,若直线l与连接A(1, -2)。B(2,1)两点的线段总有公共点,求直线l的倾斜角a与斜率k的取值范围,并说明理由.
根据题意,如图:直线l经过点P(0,-1),与连接A(1,-2),B(2,1)的线段总有公共点,则直线l的斜率必定存在,设直线l的斜率为k,则直线l的方程为y= kx-1,即kx- y-1=0 ;
9.已知点M(2, 2)和N(5, -2),点P在x轴上,且∠MPN为直角,求点P的坐标
倾斜角的定义
(1)当直线l与x轴相交时,取x轴作为基准,x轴_____与直线l向上方向之间所成的角α叫做直线l的倾斜角.
(2)当直线l与x轴平行或重合时,规定它的倾斜角为0°.直线的倾斜角α的取值范围为 ____________.
正向
直线的斜率
把一条直线的倾斜角α的_______叫做这条直线的斜率,斜率常用小写字母k表示,即k=_______.
正切值
tanα
总结
斜率公式
过两点P1(x1,y1),P2(x2,y2)(x1≠x2)的直线的斜率公式为
k=_______.
平行的判定
类型
前提条件
对应关系
图示
斜率存在
斜率不存在
总结
图示
对应关系
直线的倾斜角与斜率
理解直线倾斜角、斜率的概念
教学目标
理解并掌握直线斜率的求法
能够根据两条直线的斜率相等判断两条直线平行
能够根据两条直线的斜率之积等于-1,判断两条直线垂直
教学重点
直线斜率的求法
斜率判断两条直线的位置关系
教学难点
斜率判断两条直线的位置关系
问题1:如何确定一条直线在直角坐标系的位置呢?
两点或一点和方向
问题2:如果已知一点还需附加什么条件,才能确定直线?
一点和方向
问题3:如何表示方向?
用角
倾斜角与斜率
直线的倾斜角的定义
当直线l与x轴相交时,我们取x轴作为基准,x轴
正向与直线l向上方向之间所成的角α叫做直线的倾斜角。
α
例1下列四图中,表示直线的倾斜角的是( )
A
倾斜角的范围
规定:当直线和x轴平行或重合时, 它的倾斜角为0°
直线的斜率
定义:我们把一条直线的倾斜角α的正切值叫做这条直线的斜率.
用小写字母 k 表示,即:
由两点确定的直线的斜率:
倾斜角与斜率
倾斜角是锐角时
倾斜角与斜率
倾斜角是钝角时
直线的斜率公式:
倾斜角与斜率
(1)与两点的顺序无关,但是横坐标相同时不适用
(2)当两点横坐标相同,即直线与x轴垂直时,直线斜率不存在。(与正切函数的性质相同)
2.如图2.1-6, 已知A(3, 2), B(-4, 1), C(0,-1),求直线AB,BC, CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
3.(1)若直线的倾斜角为60°,则直线的斜率为( )
(2)已知过A(3,1),B(m,-2)的直线的斜率为1,则m的值为____.
A
0
4.如果三点A(2,1),B(-2,m),C(6,8)在同一条直线上,求实数m的值.
1.已知下列直线的倾斜角,求直线的斜率:
3.求经过下列两点的直线的斜率,并判断其倾斜角是锐角还是钝角 (1) C(18, 8),D(4, -4); (2) P(0, 0), Q(-1, 3).
4.已知a, b, c是两两不等的实数,求经过下列两点的直线的倾斜角:
(1) A(a, c), B(b,c) (2) C(a, b), D(a, c) (3) P(b, b+c), Q(a. c+a).
5.经过A(0, 2),B(-1, 0)两点的直线的方向向量为(1, k),求k的值.
理解并掌握倾斜角的概念
理解并掌握倾斜角和斜率的关系
能跟据两点坐标求出直线斜率
直线的斜率和倾斜角
两条直线平行判定
斜率存在时两直线平行.
两条直线平行的判定
此结论常用来证明三点共线
注意:上面的等价是在两直线斜率存在的前提下才
成立的,缺少这个前提,结论并不成立.
特殊情况下的两直线平行:两直线的斜率都不存在时,互相平行.
5 .已知A(2, 3), B(-4, 0),P(-3,1),Q(-1, 2),试判断直线AB与PQ的位置关系,并证明你的结论.
6.已知四边形 ABCD的四个顶点分别为A(O,0), B(2,1-1), C(4, 2), D(2, 3),试判断四边形ABCD的形状,并给出证明
理解并掌握两条直线平行的条件
能够熟练掌握直线平行条件的应用
直线的平行关系2
两条直线垂直的判定
斜率存在时两直线垂直
两条直线垂直的判定
注意:上面的等价是在两直线斜率存在的前提下才成立的,
缺少这个前提,结论并不成立.
特殊情况下的两直线垂直.
当两条直线中有一条直线斜率不存在,另一条
直线的斜率为0时,两直线垂直。
7.已知A(-6, 0),B(3, 6),P(0, 3), Q(6, -6),试判断直线AB与PQ的位置关系.
8.已知A(5, -1),B(1, 1), C(2, 3)三点,试判断△ABC的形状.
9.已知长方形ABCD的三个顶点的坐标分别为A(0,1),B(1,0),C(3,2),求第四个顶点D的坐标.
2.试确定m的值,使过A(m, 1),B(-1,m)两点的直线与过P(1,2),Q(-5, 0)两点的直线:
(1)平行; (2)垂直.
理解并掌握两条直线垂直的条件
能够熟练掌握直线垂直条件的应用
直线的垂直关系2
1.已知直线斜率的绝对值等于1,求直线的倾斜角.
直线斜率的绝对值等于1,可得直线的倾斜角为: 45° 或135°
2.已知四边形ABCD的四个顶点是A(2, 3), B(1, -1),C(-1,一2),D(一-2, 2), 求四边形ABCD的四条边所在直线的斜率.
3. m为何值时,(1)经过A(-m, 6),B(1, 3m)两点的直线的斜率是12
(2)经过A(m,2), B(-m,-2m-1)两点的直线的倾斜角是60°
4. 已知A(1, 2), B(-1. 0), C(3, 4) 三点,这三点是否在同一条直线上 为什么
8. 经过点P(0,-1)作直线1,若直线l与连接A(1, -2)。B(2,1)两点的线段总有公共点,求直线l的倾斜角a与斜率k的取值范围,并说明理由.
根据题意,如图:直线l经过点P(0,-1),与连接A(1,-2),B(2,1)的线段总有公共点,则直线l的斜率必定存在,设直线l的斜率为k,则直线l的方程为y= kx-1,即kx- y-1=0 ;
9.已知点M(2, 2)和N(5, -2),点P在x轴上,且∠MPN为直角,求点P的坐标
倾斜角的定义
(1)当直线l与x轴相交时,取x轴作为基准,x轴_____与直线l向上方向之间所成的角α叫做直线l的倾斜角.
(2)当直线l与x轴平行或重合时,规定它的倾斜角为0°.直线的倾斜角α的取值范围为 ____________.
正向
直线的斜率
把一条直线的倾斜角α的_______叫做这条直线的斜率,斜率常用小写字母k表示,即k=_______.
正切值
tanα
总结
斜率公式
过两点P1(x1,y1),P2(x2,y2)(x1≠x2)的直线的斜率公式为
k=_______.
平行的判定
类型
前提条件
对应关系
图示
斜率存在
斜率不存在
总结
图示
对应关系
