2.2 直线的方程 课件(53张PPT)
文档属性
| 名称 | 2.2 直线的方程 课件(53张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 9.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-21 23:34:03 | ||
图片预览









文档简介
(共53张PPT)
直线方程
教学目标
掌握点斜式、斜截式方程的推导过程的应用条件
理解并掌握两点式、截距式方程的公式和应用
掌握直线一般式方程
理解并掌握直线五种方程间的关系和相互转化
掌握直线方程的应用
教学重点
教学难点
掌握点斜式、斜截式方程的推导过程的应用条件
理解并掌握两点式、截距式方程的公式和应用
理解并掌握直线五种方程间的关系和相互转化
直线方程的应用
掌握点斜式、斜截式方程的推导过程的应用条件
直线方程的应用
复习
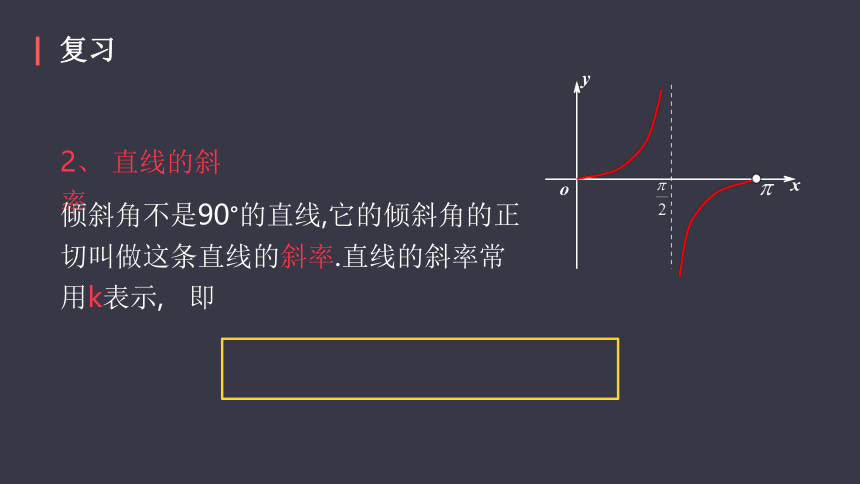
2、 直线的斜率
倾斜角不是90°的直线,它的倾斜角的正切叫做这条直线的斜率.直线的斜率常用k表示, 即
3、经过两点的斜率公式
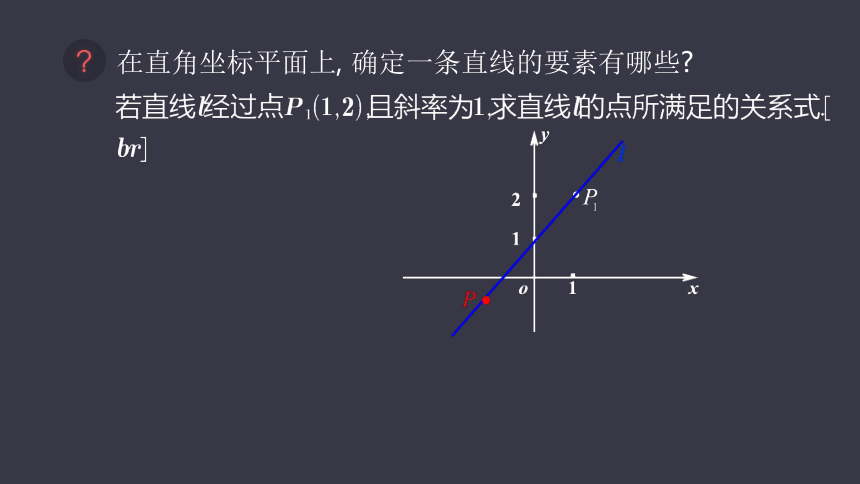
在直角坐标平面上, 确定一条直线的要素有哪些
直线方程:
一般地, 如果一条直线l上任一点的坐标(x, y)都满足一个方程, 反之, 满足该方程的每一个数对 (x, y)所确定的点都在直线l上. 我们就把这个方程称为直线l的方程.
点斜式方程:
则l的方程为:
①点斜式方程是由直线上一点和斜率确定的;
直线的点斜式方程
1.点斜式的局限性:
只能表示斜率存在的直线
2.经过点 的直线有无数条,可分两类:
即不能表示与x轴垂直的直线
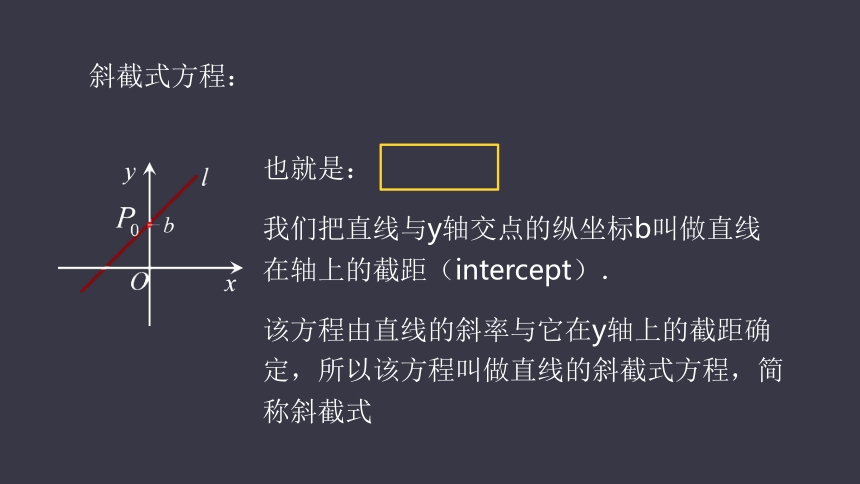
斜截式方程:
也就是:
我们把直线与y轴交点的纵坐标b叫做直线在轴上的截距(intercept).
该方程由直线的斜率与它在y轴上的截距确定,所以该方程叫做直线的斜截式方程,简称斜截式
观察方程y=kx+b,它的形式具有什么特点?
我们发现,左端y的系数恒为1,右端x的系数k和常数项b均有明显的几何意义:
k是直线的斜率,b是直线在y轴上的截距.
斜截式是点斜式的特例。只适用于斜率存在的情形。
直线在坐标轴上的横、纵截距及求法:
截距的值是实数,它是坐标值,不是距离
y=kx+b与我们学过的一次函数的表达式类似.我们知道,一次函数的图象是一条直线.你如何从直线方程的角度认识一次函数y=kx+b?一次函数中k和b的几何意义是什么?
你能说出一次函数y=2x-1,y=3x及y=-x+3图象的特点吗?
1
两点式方程
注:两点式适用于与两坐标轴不垂直的直线。
即
此结果为直线的另外一种方程
名称
截距式
已知条件
在x,y轴上的截距分别为a,b且a≠0,b≠0
示意图
方程
使用范围
斜率存在且不为0,不过原点
截距式方程
将上述四种直线方程变换一下,能否写成如下统一形式?
上述四式都可以写成直线方程的一般形式:
Ax+By+C=0, A、B不同时为0。
直线的一般式方程
一般式方程
直线的一般式与点斜式、斜截式、两点式、截距式的关系
C=0
直线l过原点:____________
直线l过点(1,1):______________
直线l平行于 轴:___________________
直线l平行于轴:____________________
A+B+C=0
A=0,B≠0,C≠0
5.设直线的方程为Ax+By+c=0(A,B不同时为零)根据下列各位置特征, 写出A,B,C应满足的关系
7.把直线l的一般式方程x-2y+6=0化为斜截式:求出直线l的斜率以及它在x轴与y轴上的截距,并画出图形.
(2)斜率为4,在y轴上的截距为-2;
解 由斜截式,得直线方程为y=4x-2,
即 4x-y-2=0.
(3)经过点A(-1,5),B(2,-1)两点;
(4)在x轴,y轴上的截距分别为-3,-1;
(5)经过点B(4,2),且平行于x轴.
解 y-2=0.
掌握直线方程的五种形式
理解并掌握直线方程的每一种形式的使用条件
直线方程的五种形式
2.判断A(1,3),B(5,7),C(10,12)三点是否共线,并说明理由.
3.已知两点A(7,-4),B(-5,6),求线段AB的垂直平分线的方程
4.已知△ABC的三个顶点A(8,5),B(4,-2),C(-6,3),求经过两边AB和AC的中点的直线方程.
5.一根弹簧,挂4N的物体时,长20cm.在弹性限度内,所挂物体的重量每增加1N,弹簧就伸长1.5cm.试写出弹簧的长度l(单位:cm)与所挂物体重量G(单位:N)之间关系的方程.
6.菱形的两条对角线分别位于x轴和y轴上,其长度分别为8和6,求菱形各边所在直线的方程
7.求经过点P(2,3),并且在两坐标轴上的截距相等的直线的方程
8.求满足下列条件的直线的方程:
(1)经过点A(3,2),且与直线4x+y-2=0平行;
(2)经过点C(2,-3)且平行于过M(1,2)和N(-1,-5)两点的直线;
(3)经过点B(3,0),且与直线2x+y-5=0垂直.
(1)由于直线4x+y-2=0的斜率为-4,则由平行的条件可得,所求直线的斜率为-4,则所求直线的方程为y-2=-4(x-3),即为4x+y-14=0;
综上所述:答案为4x+y-14=0
9.△ABC的三个顶点是A(4,0),B(6,7),C(0,3),求:
(1)边BC上的中线所在直线的方程;
(2)边BC上的高所在直线的方程;
(3)边BC的垂直平分线的方程.
10.求直线Ax+By+C=0(A,B不同时为0)的系数A,B,C分别满足什么关系时,这条直线有以下性质
(1)与两条坐标轴都相交; (2)只与x轴相交;
(3)只与y轴相交; (4)是x轴所在的直线;
(5)是y轴所在的直线
12.若直线l沿x轴向左平移3个单位长度,再沿y轴向上平移1个单位长度后,回到原来的位置,试求直线l的斜率。
13.一条光线从点P(6,4)射出,与x轴相交于点Q(2,0),经x轴反射,求入射光线和反射光线所在直线的方程.
总结
形式
斜截式
点斜式
两点式
截距式
一般式
方程
y=kx+ b
Ax+ By+C=0
已知条件
k. b
a, b
均可
限制条件
不包括k不存在时
不包括k不存在时
a≠0,b≠0
直线方程的五种形式
直线方程
教学目标
掌握点斜式、斜截式方程的推导过程的应用条件
理解并掌握两点式、截距式方程的公式和应用
掌握直线一般式方程
理解并掌握直线五种方程间的关系和相互转化
掌握直线方程的应用
教学重点
教学难点
掌握点斜式、斜截式方程的推导过程的应用条件
理解并掌握两点式、截距式方程的公式和应用
理解并掌握直线五种方程间的关系和相互转化
直线方程的应用
掌握点斜式、斜截式方程的推导过程的应用条件
直线方程的应用
复习
2、 直线的斜率
倾斜角不是90°的直线,它的倾斜角的正切叫做这条直线的斜率.直线的斜率常用k表示, 即
3、经过两点的斜率公式
在直角坐标平面上, 确定一条直线的要素有哪些
直线方程:
一般地, 如果一条直线l上任一点的坐标(x, y)都满足一个方程, 反之, 满足该方程的每一个数对 (x, y)所确定的点都在直线l上. 我们就把这个方程称为直线l的方程.
点斜式方程:
则l的方程为:
①点斜式方程是由直线上一点和斜率确定的;
直线的点斜式方程
1.点斜式的局限性:
只能表示斜率存在的直线
2.经过点 的直线有无数条,可分两类:
即不能表示与x轴垂直的直线
斜截式方程:
也就是:
我们把直线与y轴交点的纵坐标b叫做直线在轴上的截距(intercept).
该方程由直线的斜率与它在y轴上的截距确定,所以该方程叫做直线的斜截式方程,简称斜截式
观察方程y=kx+b,它的形式具有什么特点?
我们发现,左端y的系数恒为1,右端x的系数k和常数项b均有明显的几何意义:
k是直线的斜率,b是直线在y轴上的截距.
斜截式是点斜式的特例。只适用于斜率存在的情形。
直线在坐标轴上的横、纵截距及求法:
截距的值是实数,它是坐标值,不是距离
y=kx+b与我们学过的一次函数的表达式类似.我们知道,一次函数的图象是一条直线.你如何从直线方程的角度认识一次函数y=kx+b?一次函数中k和b的几何意义是什么?
你能说出一次函数y=2x-1,y=3x及y=-x+3图象的特点吗?
1
两点式方程
注:两点式适用于与两坐标轴不垂直的直线。
即
此结果为直线的另外一种方程
名称
截距式
已知条件
在x,y轴上的截距分别为a,b且a≠0,b≠0
示意图
方程
使用范围
斜率存在且不为0,不过原点
截距式方程
将上述四种直线方程变换一下,能否写成如下统一形式?
上述四式都可以写成直线方程的一般形式:
Ax+By+C=0, A、B不同时为0。
直线的一般式方程
一般式方程
直线的一般式与点斜式、斜截式、两点式、截距式的关系
C=0
直线l过原点:____________
直线l过点(1,1):______________
直线l平行于 轴:___________________
直线l平行于轴:____________________
A+B+C=0
A=0,B≠0,C≠0
5.设直线的方程为Ax+By+c=0(A,B不同时为零)根据下列各位置特征, 写出A,B,C应满足的关系
7.把直线l的一般式方程x-2y+6=0化为斜截式:求出直线l的斜率以及它在x轴与y轴上的截距,并画出图形.
(2)斜率为4,在y轴上的截距为-2;
解 由斜截式,得直线方程为y=4x-2,
即 4x-y-2=0.
(3)经过点A(-1,5),B(2,-1)两点;
(4)在x轴,y轴上的截距分别为-3,-1;
(5)经过点B(4,2),且平行于x轴.
解 y-2=0.
掌握直线方程的五种形式
理解并掌握直线方程的每一种形式的使用条件
直线方程的五种形式
2.判断A(1,3),B(5,7),C(10,12)三点是否共线,并说明理由.
3.已知两点A(7,-4),B(-5,6),求线段AB的垂直平分线的方程
4.已知△ABC的三个顶点A(8,5),B(4,-2),C(-6,3),求经过两边AB和AC的中点的直线方程.
5.一根弹簧,挂4N的物体时,长20cm.在弹性限度内,所挂物体的重量每增加1N,弹簧就伸长1.5cm.试写出弹簧的长度l(单位:cm)与所挂物体重量G(单位:N)之间关系的方程.
6.菱形的两条对角线分别位于x轴和y轴上,其长度分别为8和6,求菱形各边所在直线的方程
7.求经过点P(2,3),并且在两坐标轴上的截距相等的直线的方程
8.求满足下列条件的直线的方程:
(1)经过点A(3,2),且与直线4x+y-2=0平行;
(2)经过点C(2,-3)且平行于过M(1,2)和N(-1,-5)两点的直线;
(3)经过点B(3,0),且与直线2x+y-5=0垂直.
(1)由于直线4x+y-2=0的斜率为-4,则由平行的条件可得,所求直线的斜率为-4,则所求直线的方程为y-2=-4(x-3),即为4x+y-14=0;
综上所述:答案为4x+y-14=0
9.△ABC的三个顶点是A(4,0),B(6,7),C(0,3),求:
(1)边BC上的中线所在直线的方程;
(2)边BC上的高所在直线的方程;
(3)边BC的垂直平分线的方程.
10.求直线Ax+By+C=0(A,B不同时为0)的系数A,B,C分别满足什么关系时,这条直线有以下性质
(1)与两条坐标轴都相交; (2)只与x轴相交;
(3)只与y轴相交; (4)是x轴所在的直线;
(5)是y轴所在的直线
12.若直线l沿x轴向左平移3个单位长度,再沿y轴向上平移1个单位长度后,回到原来的位置,试求直线l的斜率。
13.一条光线从点P(6,4)射出,与x轴相交于点Q(2,0),经x轴反射,求入射光线和反射光线所在直线的方程.
总结
形式
斜截式
点斜式
两点式
截距式
一般式
方程
y=kx+ b
Ax+ By+C=0
已知条件
k. b
a, b
均可
限制条件
不包括k不存在时
不包括k不存在时
a≠0,b≠0
直线方程的五种形式
