2.5 直线与圆、圆与圆的位置 课件(76张PPT)
文档属性
| 名称 | 2.5 直线与圆、圆与圆的位置 课件(76张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 33.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-21 23:17:57 | ||
图片预览








文档简介
(共76张PPT)
直线与圆、圆与圆的位置关系
教学目标
掌握直线与圆的三种位置关系:相交、相切、相离.
会用代数法和几何法来判定直线与圆的三种位置关系.
会用直线与圆的位置关系解决一些实际问题.
理解圆与圆的位置关系的种类.
掌握圆与圆的位置关系的代数判断方法与几何判断方法,能够利用上述方法判断两圆的位置关系.
体会根据圆的对称性灵活处理问题的方法和它的优越性.
教学重点
教学难点
会用直线与圆的位置关系解决一些实际问题.
掌握圆与圆的位置关系的代数判断方法与几何判断方法,能够利用上述方法判断两圆的位置关系.
会用代数法和几何法来判定直线与圆的三种位置关系.
会用直线与圆的位置关系解决一些实际问题.
掌握圆与圆的位置关系的代数判断方法与几何判断方法,能够利用上述方法判断两圆的位置关系.
体会根据圆的对称性灵活处理问题的方法和它的优越性.
问题1:“海上生明月,天涯共此时”是唐代诗人张九龄的诗句,书写了对远方亲人的一片情深.全是情景交融,细腻入微,情真意永,感人至深.
如果我们把明月看成一个圆,海平面看成一条直线,直线与圆的位置关系由几种?
相交
相切
相离
图形
公共点个数
d与r的关系
直线的名称
2
1
0
割线
切线
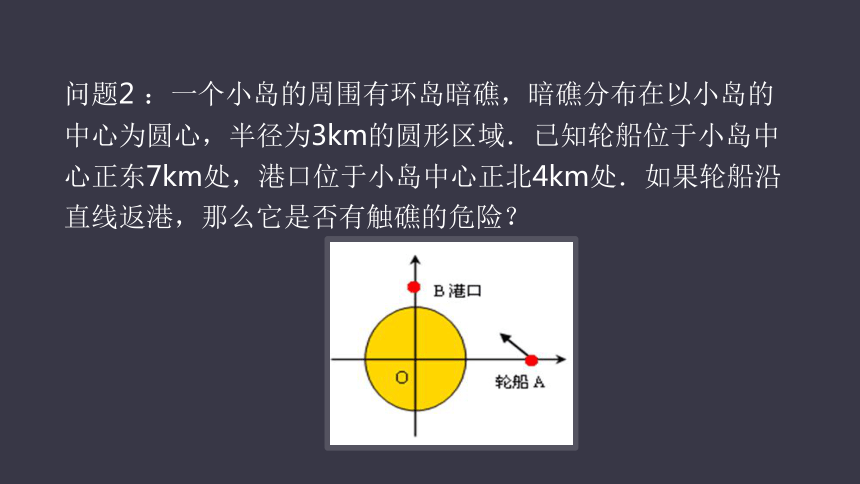
问题2 :一个小岛的周围有环岛暗礁,暗礁分布在以小岛的中心为圆心,半径为3km的圆形区域.已知轮船位于小岛中心正东7km处,港口位于小岛中心正北4km处.如果轮船沿直线返港,那么它是否有触礁的危险?
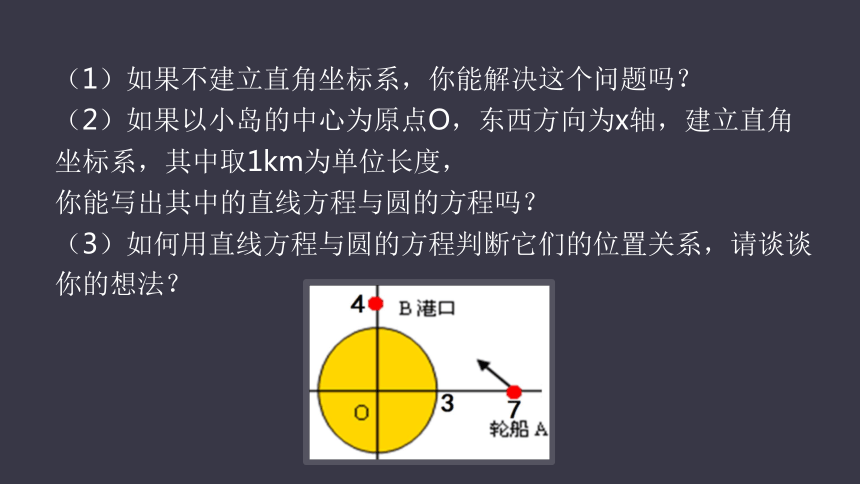
(1)如果不建立直角坐标系,你能解决这个问题吗?
(2)如果以小岛的中心为原点O,东西方向为x轴,建立直角坐标系,其中取1km为单位长度,
你能写出其中的直线方程与圆的方程吗?
(3)如何用直线方程与圆的方程判断它们的位置关系,请谈谈你的想法?
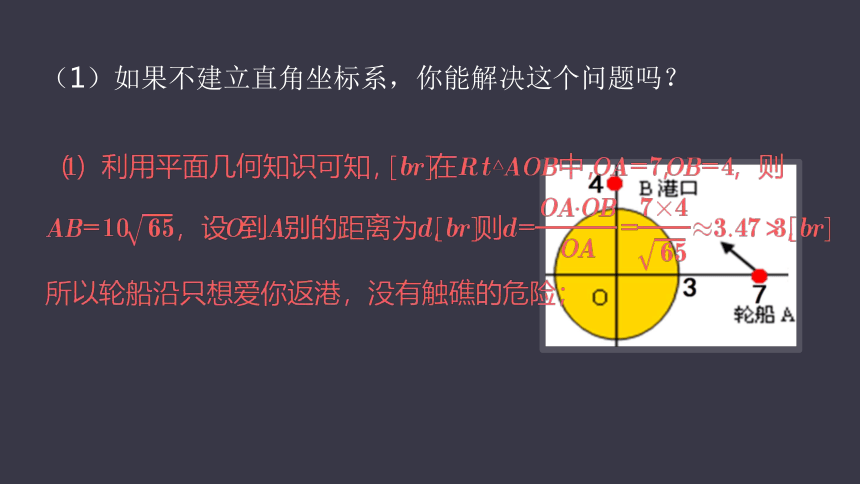
(1)如果不建立直角坐标系,你能解决这个问题吗?
(2)如果以小岛的中心为原点O,东西方向为x轴,建立直角坐标系,其中取1km为单位长度,你能写出其中的直线方程与圆的方程吗?
直线方程:
圆的方程:
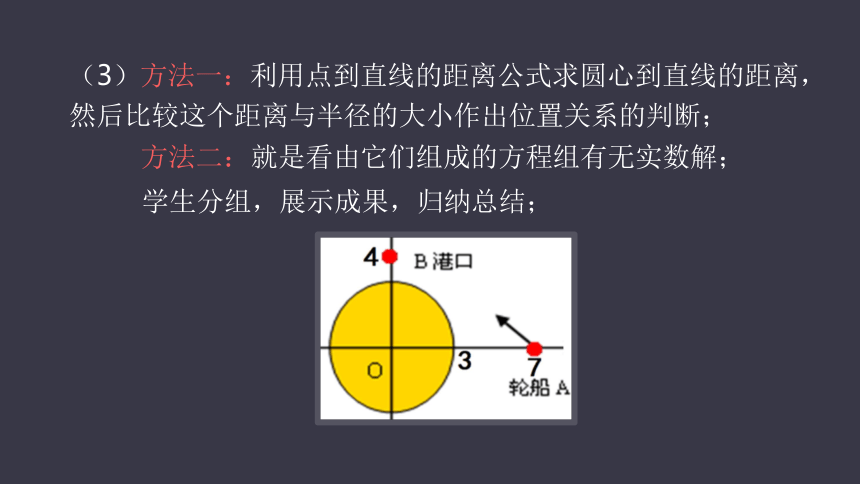
(3)方法一:利用点到直线的距离公式求圆心到直线的距离,然后比较这个距离与半径的大小作出位置关系的判断;
方法二:就是看由它们组成的方程组有无实数解;
学生分组,展示成果,归纳总结;
直线与圆的位置的关系
判断直线与圆的位置关系的方法:
方法一:判断直线l与圆的位置关系,就是看由它们的方程组成的方程组有无实数解(代数法)
代数法
位置关系
相交
相切
相离
公共点个数
0个
1个
直线与圆的位置的关系
方法二:可以依据圆心到直线的距离与半径长的关系,判断直线与圆的位置关系(几何法)
几何法
位置关系
相交
相切
相离
公共点个数
0个
1个
例题
例题
理解并掌握直线与圆的三种位置关系
理解并掌握直线与圆的位置关系的判定方法
能够运用方法判断圆与直线的位置关系
直线和圆的位置关系
弦长
(1)求直线与圆相交时的弦长有三种方法
弦长
例题
例题
例题
例题
例题
例题
熟练掌握圆中弦长的求法
圆中的弦问题
直线与圆位置关系
圆的切线求法
直线与圆位置关系
(若斜率不存在或斜率为0,则可以直接判定过定点的直线是否与圆相切,进而确定 k的取值.)
例题
例题
例题
例题
例题
例题
练习
练习
练习
例题
例题
例题
例题
练习
练习
练习
理解并掌握过圆上一点的切线方程
理解并掌握过圆外一点的切点弦方程
切线方程和切点弦方程
圆与圆的位置关系
两圆无公共点
两圆仅有一公共点
两圆有两公共点
外离
内含
内切
外切
相交
圆与圆的位置关系
方法一
将两个圆方程联立,相减,消去其中的一个未知数y或x,得关于x或y的一元二次方程.
若该方程中△>0,则两圆相交;
若方程中△=0,则两圆相切;
若方程中△<0, 两圆外离或内含.
圆与圆的位置关系转化为直线与圆位置关系
圆与圆的位置关系
圆与圆的位置关系的判定方法二:
确定圆心坐标和半径:计算圆心距
计算两圆半径和与差:比较大小解释几何位置关系
圆与圆的位置关系转化为圆心距d与R+r、|R-r|关系
方法二:
圆与圆的位置关系
圆与圆的位置关系:
例题
例题
例题
例题
例题
圆与圆的位置关系
例题
习题
习题
理解并掌握圆和圆的位置关系
理解并掌握圆和圆的位置关系的判断方法
圆和圆的位置关系
习题
习题
习题
习题
习题
习题
习题
习题
习题
习题
习题
习题
习题
习题
习题
习题
总结
位置关系
公共点个数
判断方法
几何法:设圆心到直线的距离为d=
相交
相切
相离
2
1
0
___个
___个
___个
总结
位置关系
外离
外切
相交
内切
内含
图示
总结
方程组解的个数
两圆的公共点个数
两圆的位置关系
2组
1组
0组
2个
1个
0个
相交
内切或外切
内离或外含
直线与圆、圆与圆的位置关系
教学目标
掌握直线与圆的三种位置关系:相交、相切、相离.
会用代数法和几何法来判定直线与圆的三种位置关系.
会用直线与圆的位置关系解决一些实际问题.
理解圆与圆的位置关系的种类.
掌握圆与圆的位置关系的代数判断方法与几何判断方法,能够利用上述方法判断两圆的位置关系.
体会根据圆的对称性灵活处理问题的方法和它的优越性.
教学重点
教学难点
会用直线与圆的位置关系解决一些实际问题.
掌握圆与圆的位置关系的代数判断方法与几何判断方法,能够利用上述方法判断两圆的位置关系.
会用代数法和几何法来判定直线与圆的三种位置关系.
会用直线与圆的位置关系解决一些实际问题.
掌握圆与圆的位置关系的代数判断方法与几何判断方法,能够利用上述方法判断两圆的位置关系.
体会根据圆的对称性灵活处理问题的方法和它的优越性.
问题1:“海上生明月,天涯共此时”是唐代诗人张九龄的诗句,书写了对远方亲人的一片情深.全是情景交融,细腻入微,情真意永,感人至深.
如果我们把明月看成一个圆,海平面看成一条直线,直线与圆的位置关系由几种?
相交
相切
相离
图形
公共点个数
d与r的关系
直线的名称
2
1
0
割线
切线
问题2 :一个小岛的周围有环岛暗礁,暗礁分布在以小岛的中心为圆心,半径为3km的圆形区域.已知轮船位于小岛中心正东7km处,港口位于小岛中心正北4km处.如果轮船沿直线返港,那么它是否有触礁的危险?
(1)如果不建立直角坐标系,你能解决这个问题吗?
(2)如果以小岛的中心为原点O,东西方向为x轴,建立直角坐标系,其中取1km为单位长度,
你能写出其中的直线方程与圆的方程吗?
(3)如何用直线方程与圆的方程判断它们的位置关系,请谈谈你的想法?
(1)如果不建立直角坐标系,你能解决这个问题吗?
(2)如果以小岛的中心为原点O,东西方向为x轴,建立直角坐标系,其中取1km为单位长度,你能写出其中的直线方程与圆的方程吗?
直线方程:
圆的方程:
(3)方法一:利用点到直线的距离公式求圆心到直线的距离,然后比较这个距离与半径的大小作出位置关系的判断;
方法二:就是看由它们组成的方程组有无实数解;
学生分组,展示成果,归纳总结;
直线与圆的位置的关系
判断直线与圆的位置关系的方法:
方法一:判断直线l与圆的位置关系,就是看由它们的方程组成的方程组有无实数解(代数法)
代数法
位置关系
相交
相切
相离
公共点个数
0个
1个
直线与圆的位置的关系
方法二:可以依据圆心到直线的距离与半径长的关系,判断直线与圆的位置关系(几何法)
几何法
位置关系
相交
相切
相离
公共点个数
0个
1个
例题
例题
理解并掌握直线与圆的三种位置关系
理解并掌握直线与圆的位置关系的判定方法
能够运用方法判断圆与直线的位置关系
直线和圆的位置关系
弦长
(1)求直线与圆相交时的弦长有三种方法
弦长
例题
例题
例题
例题
例题
例题
熟练掌握圆中弦长的求法
圆中的弦问题
直线与圆位置关系
圆的切线求法
直线与圆位置关系
(若斜率不存在或斜率为0,则可以直接判定过定点的直线是否与圆相切,进而确定 k的取值.)
例题
例题
例题
例题
例题
例题
练习
练习
练习
例题
例题
例题
例题
练习
练习
练习
理解并掌握过圆上一点的切线方程
理解并掌握过圆外一点的切点弦方程
切线方程和切点弦方程
圆与圆的位置关系
两圆无公共点
两圆仅有一公共点
两圆有两公共点
外离
内含
内切
外切
相交
圆与圆的位置关系
方法一
将两个圆方程联立,相减,消去其中的一个未知数y或x,得关于x或y的一元二次方程.
若该方程中△>0,则两圆相交;
若方程中△=0,则两圆相切;
若方程中△<0, 两圆外离或内含.
圆与圆的位置关系转化为直线与圆位置关系
圆与圆的位置关系
圆与圆的位置关系的判定方法二:
确定圆心坐标和半径:计算圆心距
计算两圆半径和与差:比较大小解释几何位置关系
圆与圆的位置关系转化为圆心距d与R+r、|R-r|关系
方法二:
圆与圆的位置关系
圆与圆的位置关系:
例题
例题
例题
例题
例题
圆与圆的位置关系
例题
习题
习题
理解并掌握圆和圆的位置关系
理解并掌握圆和圆的位置关系的判断方法
圆和圆的位置关系
习题
习题
习题
习题
习题
习题
习题
习题
习题
习题
习题
习题
习题
习题
习题
习题
总结
位置关系
公共点个数
判断方法
几何法:设圆心到直线的距离为d=
相交
相切
相离
2
1
0
___个
___个
___个
总结
位置关系
外离
外切
相交
内切
内含
图示
总结
方程组解的个数
两圆的公共点个数
两圆的位置关系
2组
1组
0组
2个
1个
0个
相交
内切或外切
内离或外含
