3.1 椭圆 课件(75张PPT)
文档属性
| 名称 | 3.1 椭圆 课件(75张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 13.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-21 23:19:21 | ||
图片预览










文档简介
(共75张PPT)
椭圆
掌握椭圆的定义和标准方程;
明确焦点、焦距的概念,理解椭圆标准方程的推导;
掌握椭圆的基本几何性质;
熟悉求曲线方程的一般步骤。
教学目标
掌握椭圆的标准方程,理解坐标法的基本思想
椭圆标准方程的推导和化简,坐标法的应用
教学重点
教学难点
取一条定长的细绳,把细绳的两端绑在两个图钉上,让图钉固定在两点处(有一定距离),套上笔,拉紧绳子,移动笔尖,画出的轨迹是什么曲线?
定义:平面内与两个定点 、 的距离的和等于常数(大于 | | )的点的轨迹
叫做椭圆,这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距。
定义要满足三个条件:
①平面内(这是大前提);
②任意一点到两个定点的距离的和等于常数;
③常数大于 | | .
椭圆的定义
知道了它的基本几何特征,这只是一种“定性”的描述,但是对于这种曲线还具有哪些性质,尚需进一步研究. 根据解析几何的基本思想方法,我们需要利用坐标法先建立椭圆的方程“定量”的描述,然后通过对椭圆的方程的讨论,来研究其几何性质.
1. 求曲线方程的一般步骤是什么?
2.怎样建立坐标系,才能使求出的椭圆方程最为简单?
椭圆的标准方程
1、建系
2 、设点
设M(x,y)是椭圆上的任一点
则M与| |的距离为2a
4 、让学生化简,得到
3、列出方程:
两边同除:
得
椭圆的标准方程
思考:观察图形在图中找出一些能表示a、c、
线段吗
先简化
令
,则方程变为
联想到直线截距式方程,两边同时除以
教师指出方程
在x轴上,焦点是
这里
椭圆的标准方程
叫做椭圆的标准方程.
此时椭圆的焦点
问题: 如果焦点 、 在 y 轴上,并且点O与线段 的中点重合,a、b、c 的意义同上,椭圆的方程形式又如何呢?
学生相互讨论、交流,合情猜想,动手验证可得:
指出:方程
叫做椭圆的标准方程.
在y轴上,焦点是
这里
椭圆的标准方程
此时椭圆的焦点
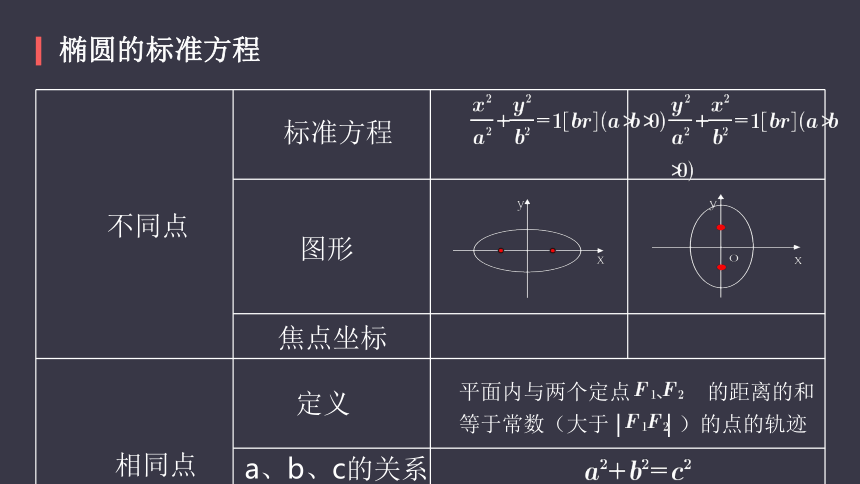
椭圆的标准方程
不同点
相同点
图形
定义
a、b、c的关系
焦点位置的判定
平面内与两个定点 的距离的和
等于常数(大于 | | )的点的轨迹
在 下面,则焦点在 x 轴上;
在 下面,则焦点在 y 轴上
标准方程
焦点坐标
已知椭圆的两个焦点坐标分别是(-2,0),(2,0),并且经过点
求它的标准方程.
解:由于椭圆的两个焦点在 x 轴上,所以设它的标准方程为
由椭圆的定义知c=2,
所以
所以
所以
,所求椭圆的标准方程为
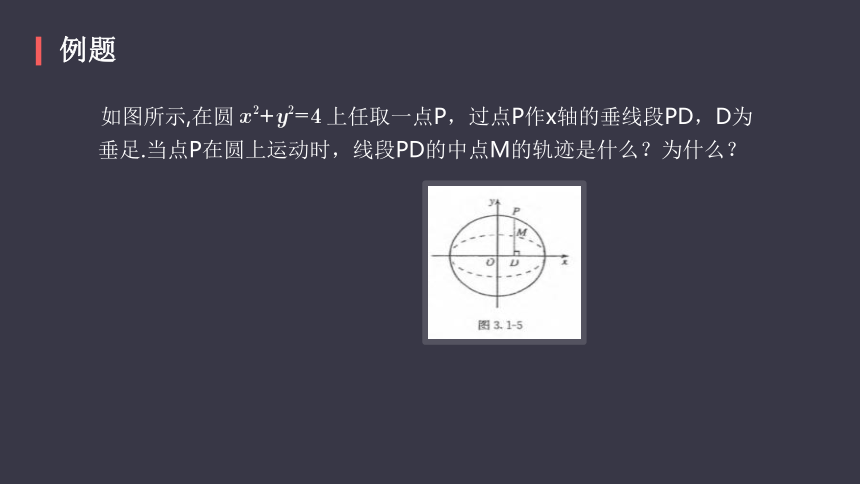
例题
如图所示,在圆
上任取一点P,过点P作x轴的垂线段PD,D为
垂足.当点P在圆上运动时,线段PD的中点M的轨迹是什么?为什么?
例题
解:设点M 的坐标为(x,y),点P 的坐标为
则点D 的坐标为
由点M是线段PD的中点,得
因为点P 在圆 上,所以
把 带入方程①,得
①
即
所以点M 的轨迹是椭圆
例题
解:设点M 的坐标为(x,y),点P 的坐标为
则点D 的坐标为
由点M是线段PD的中点,得
因为点P 在圆 上,所以
把 带入方程①,得
①
即
所以点M 的轨迹是椭圆
例题
你能从中发现圆和椭圆之间的关系吗?
“当且仅当a=b 时,c=0,这时两个焦点
重合,图形变为圆,它的方程为 ”
如图,设A,B 两点的坐标分别为(-5,0)(5,0).
直线AM,BM 相交于点M,且它们的斜率之积是
求点M的轨迹方程.
分析:设点M 的坐标为(x,y),那么直线AM,BM 的斜率就可用含 x,y 的关系式分别表示,由直线AM,BM 的斜率之积是
,可得出x,y 之间的关系式,进而得到点
M 的轨迹方程.
例题
解:设点M的坐标为(x,y),因为点A的坐标是(-5,0),
所以直线AM 的斜率
同理,直线BM 的斜率
由已知,有
化简,得点M 的轨迹方程为
点M 的轨迹是除去(-5,0),(5,0)两点的椭圆.
例题
1.如果椭圆
上一点P与焦点
的距离等于6,那么点P与
另一个焦点
的距离是
练习
2.求适合下列条件的椭圆的标准方程:
(1)a=4,b=1,焦点在x轴上;
(2)a=4, , 焦点在y轴上;
(3)a+b=10,c=
或
练习
3.经过椭圆
的右焦点 作垂直于x 轴的直线AB,
A,B 两点,
是椭圆的左焦点.
的周长
(2)如果AB 不垂直于x轴,
的周长
有变化吗?为什么?
解:由已知,a=5,b=4,所以
练习
交椭圆于
4.已知A,B 两点的坐标分别是(-1,0),(1,0),直线AM,BM 相交
于点M,且直线AM 的斜率与直线BM 的斜率的商是2,点M 的轨迹是什么?
为什么?
解:设点M 的坐标为(x,y),由已知,得
直线AM 的斜率
直线BM的斜率
由题意,得
所以,
化简,得
因此,点M 的轨迹是直线 x =-3,并去掉点(-3,0)
练习
我们知道,解析几何研究的主要问题是:
(1)根据已知条件,求曲线的方程;
(2)通过曲线的方程,研究曲线的性质.
下面,我们通过椭圆的标准方程来研究椭圆的性质:
椭圆的几何性质
1.范围
-a≤x≤a -b≤y≤b
(1)由图知:
(2)由方程:
椭圆的几何性质
2.对称性
(1)由图知:关于x 、y轴成轴对称,关于原点成中心对称。
(2)由方程:
以-x代x
y不变
以-y代y
x不变
以-x代x
-y代y
代入方程
仍成立
关于y轴对称
关于x轴对称
关于原点对称
椭圆的几何性质
3.顶点
(1)椭圆的顶点:椭圆与坐标轴的四个交点。
顶点的坐标为: (-a,0) (a,0) (0,-b) (0,b)
(2)长轴:线段 短轴:线段
长轴长:2a;长半轴长:a
短轴长:2b;短半轴长:b
(3)短轴端点、中心、焦点构成一直角Δ,且三边长为a,b,c。
椭圆的几何性质
4.离心率
(1)定义:椭圆的焦距与长轴长的比,即
叫做椭圆的离心率。
(2)范围:因为a>c>0,所以
e 越接近1,椭圆越扁;e 越接近0,椭圆越圆。
离心率反映了椭圆的扁平程度。
特别地,当a=b时,c=0,这时两个焦点重合,图形变为圆。
椭圆的几何性质
方程
图形
范围
对称性
顶点
离心率
关于x 、y轴成轴对称,关于原点成中心对称
椭圆的几何性质
求椭圆 的长轴和短轴的长、离心率、焦点和顶点的坐标.
解:把原方程化为标准方程,得
于是a=5,b=4,
因此,椭圆的长轴和短轴的长分别是2a=10和2b=8,离心率
两个焦点坐标分别是 和
四个顶点坐标分别是
和
例题
1.你能用圆规作出图中椭圆焦点的位置吗?你的依据是什么?
练习
1.你能用圆规作出图中椭圆焦点的位置吗?你的依据是什么?
以点 (或点 )为圆心,以线段 (或 )为半径画圆,
圆与x轴的两个交点分别为
点 就是椭圆的两个焦点
这是因为,在 中,
所以,
同样有
练习
2.求下列椭圆的焦点坐标
(1)焦点坐标为(-8,0),(8,0)
(2)焦点坐标为(0,2),(0,-2)
练习
3.求适合下列条件的椭圆的标准方程
(1)焦点在 x 轴上,
(2)焦点在 y 轴上,
练习
4.求适合下列条件的椭圆的标准方程
(1)经过P(-3,0),Q(0,-2)两点
(2)长轴长等于20,离心率等于
或
练习
5.比较下列每组中椭圆的形状,哪一个更接近于圆?为什么?
与
与
(1)椭圆 的离心率是 ,椭圆 的离心率是
因为 ,所以,椭圆 更圆,椭圆 更扁
(2)椭圆 的离心率是 ,椭圆 的离心率是
因为 ,所以,椭圆 更圆,椭圆 更扁
练习
如图,一种电影放映灯泡的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周
形成的曲面) 的一部分。过对称轴的截口ABC是椭圆的一部分,灯丝位于椭圆的
一个焦点
上,片门位于另一个焦点
上,由椭圆一个焦点
发出的光线,
经过
旋转椭圆面反射后集中到另一个焦点
.已知
求截口ABC所在椭圆的方程。(精确到0.1cm)
练习
解:建立如图所示的平面直角坐标系,设所求椭圆方程为
在 中,
由椭圆的性质知,
所以,
所以,所求的椭圆方程为
例题
动点M(x.y)与定点F(4,0)的距离和M到定直线l:
的距离的比是常数 ,求动点M 的轨迹
例题
如图,设d是点M到直线l: 的距离,
根据题意,动点M的轨迹集合
由此得
将上式两边平方,并化简,得
即
所以,点M 的轨迹是长轴、短轴长分别为10,6的椭圆
例题
一般地,若点M(x,y)与定点
的距离和它到定直线l:
的距离之比为常数
则点M的轨迹是椭圆.定点
是椭圆的一个焦点,
直线l叫做椭圆的准线.
拓展:椭圆的第二定义
设M 是椭圆上任意一点,则
对左焦点和左准线有:
对右焦点和右准线有:
拓展:椭圆的第二定义
掌握椭圆第二定义的意义和应用
椭圆的第二定义
如图,已知直线l:4x-5y+m=0和椭圆C:
m为何值时,直线l与椭圆C:
(1)有两个公共点?
(2)有且仅有一个公共点?
(3)没有公共点?
例题
分析:直线l与椭圆C 的公共点的个数与方程组
解的个数相对应.
所以,我们可以通过判断上述方程组解的情况得到问题的解答
解:由方程组
消去y,得
①
方程①的根的判别式
由 ,得
由 ,得
由 ,得
此时方程①有两个不相等的实数根,直线l与椭圆C有两个不同的公共点
此时方程①有两个相等的实数根,直线l与椭圆C有且只有一个公共点
此时方程①没有实数根,直线l与椭圆C 没有公共点
或
例题
1.求下列直线与椭圆的交点坐标
练习
2.经过椭圆 的左焦点
作倾斜角为 的直线l,
直线l与椭圆相交于A,B 两点,求线段AB 的长
练习
1.如果点M(x,y)在运动过程中,总满足关系式
那么点M 的轨迹是什么曲线?为什么?写出它的方程
解:由点M(x,y)满足的关系式
以及椭圆的定义得,点M 的轨迹是以 为焦点,
长轴长为10的椭圆
它的方程是
习题
2.写出适合下列条件的椭圆的标准方程
(1)焦点坐标分别为(0,-4),(0,4),a=5
(2)a+c=10,a-c=4
或
习题
3.求下列椭圆的长轴和短轴长、离心率、焦点坐标、顶点坐标,并画出图形
(1)长轴长2a=8,短轴长2b=4,离心率 ,
焦点坐标分别是
顶点坐标分别是
(2)长轴长2a=18,短轴长2b=6,离心率 ,
顶点坐标分别是
焦点坐标分别是
(0,-9),(0,9),(-3,0),(3,0)
习题
4.求适合下列条件的椭圆的标准方程
(1)经过 两点
(2)长轴长是短轴长的3倍,且经过点P(3,0)
(3)焦距是8,离心率等于0.8
或
或
习题
5.已知P是椭圆 上的一点,且以点P及焦点 为顶点的
三角形的面积等于1,
求点P 的坐标
解:由已知,椭圆的焦距
因为 的面积等于1,所以,
解得
代入椭圆的方程,得
解得
所以,点P 的坐标是 ,共有4个
习题
6.如图,圆O的半径为定长r,A是圆O内一个定点,P是圆O上任意一点.
线段AP的垂直平分线l和半径OP相交于点Q,当点P在圆上运动时,点Q
的轨迹是什么? 为什么?
解:如图,连接QA
由已知,得|QA|=|QP|
所以,|QO|+|QA|=|QO|+|QP|=|OP|=r
又因为点A在圆内,所以|OA|<|OP|
根据椭圆的定义,点Q的轨迹是以O,A为焦点,r为长轴长的椭圆
习题
7.慧星“紫金山一号”是南京紫金山天文台发现的,它的运行轨道是以太阳为一个
焦点的椭圆,测得轨道的近日点(距离太阳最近的点)距太阳中心1.486 天文单
位,远日点(距离太阳最远的点)距太阳中心5.563天文单位(1天文单位是太阳
到地球的平均距离,约
),且近日点、远日点及太阳中心
线上,求轨迹方程.
在同一条直
习题
8.点M与定点F(2,0)的距离和它到定直线x=8的距离的比是1:2,求点M
的轨迹方程,并说明轨迹是什么图形
解:设d到点M到直线x=8的距离,根据题意,所求轨迹就是集合
由此得
将上式两边平方,并化简,得
即
所以,点M的轨迹是长轴,短轴长分别是8, 的椭圆
习题
9.如图, ,垂足为D,点M 在DP 的延长线上,且
轴
当点P在圆 上运动时,
并说明轨迹的形状
求点M 的轨迹
方程,
习题
解:设点M 的坐标为(x,y),点P的坐标为 ,则
所以,
因为点P 在圆上,所以
①
②
将①代入②,得点M 的轨迹方程为
即
所以点M 的轨迹是一个椭圆.
与例2相比可见,椭圆也可以看作是由圆沿某个方向压缩或拉伸得到
习题
10.一动圆与圆
外切,同时与圆
内切,
求动圆圆心的轨迹方程,并说明它是什么曲线.
设动圆圆心为P(x,y),半径为R,两已知圆的圆心分别为
分别将两已知圆的方程
配方,得
①②两式的两边分别相加,得
化简方程③,先移项,再两边分别平方,并整理,得
将④两边分别平方,并整理,得
将常数项移至方程的右边,两边分别除以108,得
由方程⑥可知,动圆圆心的轨迹是椭圆,它的长轴和短轴长为12,
习题
10.一动圆与圆
外切,同时与圆
内切,
求动圆圆心的轨迹方程,并说明它是什么曲线.
习题
解法二:同解法一,得方程
由方程①可知,动圆圆心P(x,y)到点
的距离的和是常数12,所以点P 的轨迹是焦点为(-3,0),(3,0)
,长轴长等于12 的椭圆.并且这个椭圆的中心与坐标原点重合,焦点在
x 轴上,于是可求出它的标准方程.
因为 2c=6,2a=12, 所以 c=3,a=6,
于是,动圆圆心的轨迹方程为
所以
11.如图,矩形ABCD中, E,F,G,H分别是
是矩形四条边的中点,R,S,T是线段OF 的四等分点, 是线段CF 的四
、ES与
ET与 的交点L,M,N 都
在椭圆
上
习题
等分点.证明直线ER与
11.如图,矩形ABCD中, E,F,G,H分别是
是矩形四条边的中点,R,S,T是线段OF 的四等分点, 是线段CF 的四
、ES与
ET与 的交点L,M,N 都
在椭圆
上
解:如图,由已知,得E(0,-3),F(4,0),G(0,3),H(-4,0).
因为R,S,T是线段OF 的四等分点, 是线段CF 的四等分点
所以,R(1,0),S(2,0),T(3,0);
直线ER的方程是y=3x-3;
直线 的方程是
联立这两个方程,解得
所以,点L的坐标为
同样,点M 的坐标为
点N 的坐标为
习题
等分点.证明直线ER与
11.如图,矩形ABCD中, E,F,G,H分别是
是矩形四条边的中点,R,S,T是线段OF 的四等分点, 是线段CF 的四
、ES与
ET与 的交点L,M,N 都
在椭圆
上
习题
等分点.证明直线ER与
由作图可见,可以设椭圆的方程为
把点L,M 的坐标代入方程①,并解方程组,得
所以经过点L,M 的椭圆方程为
把点N 的坐标代入 ,得
所以点N 在椭圆 上
因此点L,M 都在椭圆 上
12.已知地球运行的轨道是长半轴长 ,离心率 的椭圆,
且太阳在这个椭圆的一个焦点上,求地球到太阳的最大和最小距离
地球到太阳的最大距离为
,最小距离为
习题
13.已知椭圆 ,直线l: 4x-5y+40.椭圆上是否存在一点,使得:
(1)它到直线l 的距离最小?最小距离是多少?
(2)它到直线l 的距离最大?最大距离是多少?
习题
14.已知椭圆 ,一组平行直线的斜率是
(1)这组直线何时与椭圆相交?
(2)当它们与椭圆相交时,证明这些直线被椭圆截的线段的中点在同一条直线
解:设这组平行线的方程为
把 带入椭圆方程 ,得
这个方程根的判别式
(1)由 ,得
当这组直线在y轴上的截距的取值范围是 时,直线与椭圆相交
(2)设直线与椭圆相交得到线段AB,并设线段AB的中点为
则
因为点M 在直线 上,与
联立,消去m, 得3x+2y=0
这说明点M 的轨迹是这条直线被椭圆截下的弦(不包括端点),这些弦的中点在一条直线上
习题
上.
1.焦半径公式
时, 最大为
时, 最小为
时, 最小为
时, 最大为
a+c
a-c
a+c
a-c
拓展:焦点三角形
(1)周长=2c+2a;
(2)面积=
最大面积=bc;
(3)越靠近短轴顶点时, 越大;
(4)
拓展:焦点三角形
椭圆 的两个焦点为 ,点P 在椭圆上,若
则点P 到 x 轴的距离为
拓展:焦点三角形
解: 椭圆方程 ,
可得
设
得
则有
的面积
设点I 到 x 轴的距离为h,则
故答案为:
拓展:焦点三角形
即
椭圆 的两个焦点为 ,点P 在椭圆上,若
则点P 到 x 轴的距离为
(1)椭圆 的焦点为 ,点P
在椭圆上,若
则 的大小为
(2)已知椭圆 中,点P是椭圆上一点,
焦点,且
,则 的面积为
拓展:焦点三角形
是椭圆的
[解析] (1)由 ,知 ,
拓展:焦点三角形
(2)由 ,可知 ,所以 ,从而
|
|
=2c=2.
在 中,由余弦定理得
①
②
由椭圆定义得
即
由①②联立可得
所以
拓展:焦点三角形
掌握焦点三角形的基本性质和用法
椭圆的焦点三角形
随堂试题
2
C
随堂试题
·
A.2 B.3 C.6 D.8
(1)C (2)7
随堂试题
5.已知椭圆的中心在原点,对称轴为坐标轴,长半轴长与短半轴
长的和为 ,离心率为 ,则椭圆的标准方程为
或
随堂试题
椭圆
1.椭圆的定义
2.椭圆标准方程的建立
3.椭圆的简单几何性质:x,y的取值范围;对称性;顶点;离心率
4.焦点三角形性质的应用
总结
椭圆
掌握椭圆的定义和标准方程;
明确焦点、焦距的概念,理解椭圆标准方程的推导;
掌握椭圆的基本几何性质;
熟悉求曲线方程的一般步骤。
教学目标
掌握椭圆的标准方程,理解坐标法的基本思想
椭圆标准方程的推导和化简,坐标法的应用
教学重点
教学难点
取一条定长的细绳,把细绳的两端绑在两个图钉上,让图钉固定在两点处(有一定距离),套上笔,拉紧绳子,移动笔尖,画出的轨迹是什么曲线?
定义:平面内与两个定点 、 的距离的和等于常数(大于 | | )的点的轨迹
叫做椭圆,这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距。
定义要满足三个条件:
①平面内(这是大前提);
②任意一点到两个定点的距离的和等于常数;
③常数大于 | | .
椭圆的定义
知道了它的基本几何特征,这只是一种“定性”的描述,但是对于这种曲线还具有哪些性质,尚需进一步研究. 根据解析几何的基本思想方法,我们需要利用坐标法先建立椭圆的方程“定量”的描述,然后通过对椭圆的方程的讨论,来研究其几何性质.
1. 求曲线方程的一般步骤是什么?
2.怎样建立坐标系,才能使求出的椭圆方程最为简单?
椭圆的标准方程
1、建系
2 、设点
设M(x,y)是椭圆上的任一点
则M与| |的距离为2a
4 、让学生化简,得到
3、列出方程:
两边同除:
得
椭圆的标准方程
思考:观察图形在图中找出一些能表示a、c、
线段吗
先简化
令
,则方程变为
联想到直线截距式方程,两边同时除以
教师指出方程
在x轴上,焦点是
这里
椭圆的标准方程
叫做椭圆的标准方程.
此时椭圆的焦点
问题: 如果焦点 、 在 y 轴上,并且点O与线段 的中点重合,a、b、c 的意义同上,椭圆的方程形式又如何呢?
学生相互讨论、交流,合情猜想,动手验证可得:
指出:方程
叫做椭圆的标准方程.
在y轴上,焦点是
这里
椭圆的标准方程
此时椭圆的焦点
椭圆的标准方程
不同点
相同点
图形
定义
a、b、c的关系
焦点位置的判定
平面内与两个定点 的距离的和
等于常数(大于 | | )的点的轨迹
在 下面,则焦点在 x 轴上;
在 下面,则焦点在 y 轴上
标准方程
焦点坐标
已知椭圆的两个焦点坐标分别是(-2,0),(2,0),并且经过点
求它的标准方程.
解:由于椭圆的两个焦点在 x 轴上,所以设它的标准方程为
由椭圆的定义知c=2,
所以
所以
所以
,所求椭圆的标准方程为
例题
如图所示,在圆
上任取一点P,过点P作x轴的垂线段PD,D为
垂足.当点P在圆上运动时,线段PD的中点M的轨迹是什么?为什么?
例题
解:设点M 的坐标为(x,y),点P 的坐标为
则点D 的坐标为
由点M是线段PD的中点,得
因为点P 在圆 上,所以
把 带入方程①,得
①
即
所以点M 的轨迹是椭圆
例题
解:设点M 的坐标为(x,y),点P 的坐标为
则点D 的坐标为
由点M是线段PD的中点,得
因为点P 在圆 上,所以
把 带入方程①,得
①
即
所以点M 的轨迹是椭圆
例题
你能从中发现圆和椭圆之间的关系吗?
“当且仅当a=b 时,c=0,这时两个焦点
重合,图形变为圆,它的方程为 ”
如图,设A,B 两点的坐标分别为(-5,0)(5,0).
直线AM,BM 相交于点M,且它们的斜率之积是
求点M的轨迹方程.
分析:设点M 的坐标为(x,y),那么直线AM,BM 的斜率就可用含 x,y 的关系式分别表示,由直线AM,BM 的斜率之积是
,可得出x,y 之间的关系式,进而得到点
M 的轨迹方程.
例题
解:设点M的坐标为(x,y),因为点A的坐标是(-5,0),
所以直线AM 的斜率
同理,直线BM 的斜率
由已知,有
化简,得点M 的轨迹方程为
点M 的轨迹是除去(-5,0),(5,0)两点的椭圆.
例题
1.如果椭圆
上一点P与焦点
的距离等于6,那么点P与
另一个焦点
的距离是
练习
2.求适合下列条件的椭圆的标准方程:
(1)a=4,b=1,焦点在x轴上;
(2)a=4, , 焦点在y轴上;
(3)a+b=10,c=
或
练习
3.经过椭圆
的右焦点 作垂直于x 轴的直线AB,
A,B 两点,
是椭圆的左焦点.
的周长
(2)如果AB 不垂直于x轴,
的周长
有变化吗?为什么?
解:由已知,a=5,b=4,所以
练习
交椭圆于
4.已知A,B 两点的坐标分别是(-1,0),(1,0),直线AM,BM 相交
于点M,且直线AM 的斜率与直线BM 的斜率的商是2,点M 的轨迹是什么?
为什么?
解:设点M 的坐标为(x,y),由已知,得
直线AM 的斜率
直线BM的斜率
由题意,得
所以,
化简,得
因此,点M 的轨迹是直线 x =-3,并去掉点(-3,0)
练习
我们知道,解析几何研究的主要问题是:
(1)根据已知条件,求曲线的方程;
(2)通过曲线的方程,研究曲线的性质.
下面,我们通过椭圆的标准方程来研究椭圆的性质:
椭圆的几何性质
1.范围
-a≤x≤a -b≤y≤b
(1)由图知:
(2)由方程:
椭圆的几何性质
2.对称性
(1)由图知:关于x 、y轴成轴对称,关于原点成中心对称。
(2)由方程:
以-x代x
y不变
以-y代y
x不变
以-x代x
-y代y
代入方程
仍成立
关于y轴对称
关于x轴对称
关于原点对称
椭圆的几何性质
3.顶点
(1)椭圆的顶点:椭圆与坐标轴的四个交点。
顶点的坐标为: (-a,0) (a,0) (0,-b) (0,b)
(2)长轴:线段 短轴:线段
长轴长:2a;长半轴长:a
短轴长:2b;短半轴长:b
(3)短轴端点、中心、焦点构成一直角Δ,且三边长为a,b,c。
椭圆的几何性质
4.离心率
(1)定义:椭圆的焦距与长轴长的比,即
叫做椭圆的离心率。
(2)范围:因为a>c>0,所以
e 越接近1,椭圆越扁;e 越接近0,椭圆越圆。
离心率反映了椭圆的扁平程度。
特别地,当a=b时,c=0,这时两个焦点重合,图形变为圆。
椭圆的几何性质
方程
图形
范围
对称性
顶点
离心率
关于x 、y轴成轴对称,关于原点成中心对称
椭圆的几何性质
求椭圆 的长轴和短轴的长、离心率、焦点和顶点的坐标.
解:把原方程化为标准方程,得
于是a=5,b=4,
因此,椭圆的长轴和短轴的长分别是2a=10和2b=8,离心率
两个焦点坐标分别是 和
四个顶点坐标分别是
和
例题
1.你能用圆规作出图中椭圆焦点的位置吗?你的依据是什么?
练习
1.你能用圆规作出图中椭圆焦点的位置吗?你的依据是什么?
以点 (或点 )为圆心,以线段 (或 )为半径画圆,
圆与x轴的两个交点分别为
点 就是椭圆的两个焦点
这是因为,在 中,
所以,
同样有
练习
2.求下列椭圆的焦点坐标
(1)焦点坐标为(-8,0),(8,0)
(2)焦点坐标为(0,2),(0,-2)
练习
3.求适合下列条件的椭圆的标准方程
(1)焦点在 x 轴上,
(2)焦点在 y 轴上,
练习
4.求适合下列条件的椭圆的标准方程
(1)经过P(-3,0),Q(0,-2)两点
(2)长轴长等于20,离心率等于
或
练习
5.比较下列每组中椭圆的形状,哪一个更接近于圆?为什么?
与
与
(1)椭圆 的离心率是 ,椭圆 的离心率是
因为 ,所以,椭圆 更圆,椭圆 更扁
(2)椭圆 的离心率是 ,椭圆 的离心率是
因为 ,所以,椭圆 更圆,椭圆 更扁
练习
如图,一种电影放映灯泡的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周
形成的曲面) 的一部分。过对称轴的截口ABC是椭圆的一部分,灯丝位于椭圆的
一个焦点
上,片门位于另一个焦点
上,由椭圆一个焦点
发出的光线,
经过
旋转椭圆面反射后集中到另一个焦点
.已知
求截口ABC所在椭圆的方程。(精确到0.1cm)
练习
解:建立如图所示的平面直角坐标系,设所求椭圆方程为
在 中,
由椭圆的性质知,
所以,
所以,所求的椭圆方程为
例题
动点M(x.y)与定点F(4,0)的距离和M到定直线l:
的距离的比是常数 ,求动点M 的轨迹
例题
如图,设d是点M到直线l: 的距离,
根据题意,动点M的轨迹集合
由此得
将上式两边平方,并化简,得
即
所以,点M 的轨迹是长轴、短轴长分别为10,6的椭圆
例题
一般地,若点M(x,y)与定点
的距离和它到定直线l:
的距离之比为常数
则点M的轨迹是椭圆.定点
是椭圆的一个焦点,
直线l叫做椭圆的准线.
拓展:椭圆的第二定义
设M 是椭圆上任意一点,则
对左焦点和左准线有:
对右焦点和右准线有:
拓展:椭圆的第二定义
掌握椭圆第二定义的意义和应用
椭圆的第二定义
如图,已知直线l:4x-5y+m=0和椭圆C:
m为何值时,直线l与椭圆C:
(1)有两个公共点?
(2)有且仅有一个公共点?
(3)没有公共点?
例题
分析:直线l与椭圆C 的公共点的个数与方程组
解的个数相对应.
所以,我们可以通过判断上述方程组解的情况得到问题的解答
解:由方程组
消去y,得
①
方程①的根的判别式
由 ,得
由 ,得
由 ,得
此时方程①有两个不相等的实数根,直线l与椭圆C有两个不同的公共点
此时方程①有两个相等的实数根,直线l与椭圆C有且只有一个公共点
此时方程①没有实数根,直线l与椭圆C 没有公共点
或
例题
1.求下列直线与椭圆的交点坐标
练习
2.经过椭圆 的左焦点
作倾斜角为 的直线l,
直线l与椭圆相交于A,B 两点,求线段AB 的长
练习
1.如果点M(x,y)在运动过程中,总满足关系式
那么点M 的轨迹是什么曲线?为什么?写出它的方程
解:由点M(x,y)满足的关系式
以及椭圆的定义得,点M 的轨迹是以 为焦点,
长轴长为10的椭圆
它的方程是
习题
2.写出适合下列条件的椭圆的标准方程
(1)焦点坐标分别为(0,-4),(0,4),a=5
(2)a+c=10,a-c=4
或
习题
3.求下列椭圆的长轴和短轴长、离心率、焦点坐标、顶点坐标,并画出图形
(1)长轴长2a=8,短轴长2b=4,离心率 ,
焦点坐标分别是
顶点坐标分别是
(2)长轴长2a=18,短轴长2b=6,离心率 ,
顶点坐标分别是
焦点坐标分别是
(0,-9),(0,9),(-3,0),(3,0)
习题
4.求适合下列条件的椭圆的标准方程
(1)经过 两点
(2)长轴长是短轴长的3倍,且经过点P(3,0)
(3)焦距是8,离心率等于0.8
或
或
习题
5.已知P是椭圆 上的一点,且以点P及焦点 为顶点的
三角形的面积等于1,
求点P 的坐标
解:由已知,椭圆的焦距
因为 的面积等于1,所以,
解得
代入椭圆的方程,得
解得
所以,点P 的坐标是 ,共有4个
习题
6.如图,圆O的半径为定长r,A是圆O内一个定点,P是圆O上任意一点.
线段AP的垂直平分线l和半径OP相交于点Q,当点P在圆上运动时,点Q
的轨迹是什么? 为什么?
解:如图,连接QA
由已知,得|QA|=|QP|
所以,|QO|+|QA|=|QO|+|QP|=|OP|=r
又因为点A在圆内,所以|OA|<|OP|
根据椭圆的定义,点Q的轨迹是以O,A为焦点,r为长轴长的椭圆
习题
7.慧星“紫金山一号”是南京紫金山天文台发现的,它的运行轨道是以太阳为一个
焦点的椭圆,测得轨道的近日点(距离太阳最近的点)距太阳中心1.486 天文单
位,远日点(距离太阳最远的点)距太阳中心5.563天文单位(1天文单位是太阳
到地球的平均距离,约
),且近日点、远日点及太阳中心
线上,求轨迹方程.
在同一条直
习题
8.点M与定点F(2,0)的距离和它到定直线x=8的距离的比是1:2,求点M
的轨迹方程,并说明轨迹是什么图形
解:设d到点M到直线x=8的距离,根据题意,所求轨迹就是集合
由此得
将上式两边平方,并化简,得
即
所以,点M的轨迹是长轴,短轴长分别是8, 的椭圆
习题
9.如图, ,垂足为D,点M 在DP 的延长线上,且
轴
当点P在圆 上运动时,
并说明轨迹的形状
求点M 的轨迹
方程,
习题
解:设点M 的坐标为(x,y),点P的坐标为 ,则
所以,
因为点P 在圆上,所以
①
②
将①代入②,得点M 的轨迹方程为
即
所以点M 的轨迹是一个椭圆.
与例2相比可见,椭圆也可以看作是由圆沿某个方向压缩或拉伸得到
习题
10.一动圆与圆
外切,同时与圆
内切,
求动圆圆心的轨迹方程,并说明它是什么曲线.
设动圆圆心为P(x,y),半径为R,两已知圆的圆心分别为
分别将两已知圆的方程
配方,得
①②两式的两边分别相加,得
化简方程③,先移项,再两边分别平方,并整理,得
将④两边分别平方,并整理,得
将常数项移至方程的右边,两边分别除以108,得
由方程⑥可知,动圆圆心的轨迹是椭圆,它的长轴和短轴长为12,
习题
10.一动圆与圆
外切,同时与圆
内切,
求动圆圆心的轨迹方程,并说明它是什么曲线.
习题
解法二:同解法一,得方程
由方程①可知,动圆圆心P(x,y)到点
的距离的和是常数12,所以点P 的轨迹是焦点为(-3,0),(3,0)
,长轴长等于12 的椭圆.并且这个椭圆的中心与坐标原点重合,焦点在
x 轴上,于是可求出它的标准方程.
因为 2c=6,2a=12, 所以 c=3,a=6,
于是,动圆圆心的轨迹方程为
所以
11.如图,矩形ABCD中, E,F,G,H分别是
是矩形四条边的中点,R,S,T是线段OF 的四等分点, 是线段CF 的四
、ES与
ET与 的交点L,M,N 都
在椭圆
上
习题
等分点.证明直线ER与
11.如图,矩形ABCD中, E,F,G,H分别是
是矩形四条边的中点,R,S,T是线段OF 的四等分点, 是线段CF 的四
、ES与
ET与 的交点L,M,N 都
在椭圆
上
解:如图,由已知,得E(0,-3),F(4,0),G(0,3),H(-4,0).
因为R,S,T是线段OF 的四等分点, 是线段CF 的四等分点
所以,R(1,0),S(2,0),T(3,0);
直线ER的方程是y=3x-3;
直线 的方程是
联立这两个方程,解得
所以,点L的坐标为
同样,点M 的坐标为
点N 的坐标为
习题
等分点.证明直线ER与
11.如图,矩形ABCD中, E,F,G,H分别是
是矩形四条边的中点,R,S,T是线段OF 的四等分点, 是线段CF 的四
、ES与
ET与 的交点L,M,N 都
在椭圆
上
习题
等分点.证明直线ER与
由作图可见,可以设椭圆的方程为
把点L,M 的坐标代入方程①,并解方程组,得
所以经过点L,M 的椭圆方程为
把点N 的坐标代入 ,得
所以点N 在椭圆 上
因此点L,M 都在椭圆 上
12.已知地球运行的轨道是长半轴长 ,离心率 的椭圆,
且太阳在这个椭圆的一个焦点上,求地球到太阳的最大和最小距离
地球到太阳的最大距离为
,最小距离为
习题
13.已知椭圆 ,直线l: 4x-5y+40.椭圆上是否存在一点,使得:
(1)它到直线l 的距离最小?最小距离是多少?
(2)它到直线l 的距离最大?最大距离是多少?
习题
14.已知椭圆 ,一组平行直线的斜率是
(1)这组直线何时与椭圆相交?
(2)当它们与椭圆相交时,证明这些直线被椭圆截的线段的中点在同一条直线
解:设这组平行线的方程为
把 带入椭圆方程 ,得
这个方程根的判别式
(1)由 ,得
当这组直线在y轴上的截距的取值范围是 时,直线与椭圆相交
(2)设直线与椭圆相交得到线段AB,并设线段AB的中点为
则
因为点M 在直线 上,与
联立,消去m, 得3x+2y=0
这说明点M 的轨迹是这条直线被椭圆截下的弦(不包括端点),这些弦的中点在一条直线上
习题
上.
1.焦半径公式
时, 最大为
时, 最小为
时, 最小为
时, 最大为
a+c
a-c
a+c
a-c
拓展:焦点三角形
(1)周长=2c+2a;
(2)面积=
最大面积=bc;
(3)越靠近短轴顶点时, 越大;
(4)
拓展:焦点三角形
椭圆 的两个焦点为 ,点P 在椭圆上,若
则点P 到 x 轴的距离为
拓展:焦点三角形
解: 椭圆方程 ,
可得
设
得
则有
的面积
设点I 到 x 轴的距离为h,则
故答案为:
拓展:焦点三角形
即
椭圆 的两个焦点为 ,点P 在椭圆上,若
则点P 到 x 轴的距离为
(1)椭圆 的焦点为 ,点P
在椭圆上,若
则 的大小为
(2)已知椭圆 中,点P是椭圆上一点,
焦点,且
,则 的面积为
拓展:焦点三角形
是椭圆的
[解析] (1)由 ,知 ,
拓展:焦点三角形
(2)由 ,可知 ,所以 ,从而
|
|
=2c=2.
在 中,由余弦定理得
①
②
由椭圆定义得
即
由①②联立可得
所以
拓展:焦点三角形
掌握焦点三角形的基本性质和用法
椭圆的焦点三角形
随堂试题
2
C
随堂试题
·
A.2 B.3 C.6 D.8
(1)C (2)7
随堂试题
5.已知椭圆的中心在原点,对称轴为坐标轴,长半轴长与短半轴
长的和为 ,离心率为 ,则椭圆的标准方程为
或
随堂试题
椭圆
1.椭圆的定义
2.椭圆标准方程的建立
3.椭圆的简单几何性质:x,y的取值范围;对称性;顶点;离心率
4.焦点三角形性质的应用
总结
