7.2 复数的四则运算 课件(31张PPT)
文档属性
| 名称 | 7.2 复数的四则运算 课件(31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 370.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-21 23:36:34 | ||
图片预览










文档简介
(共31张PPT)
复数的四则运算
掌握复数代数形式的加法、减法、乘法和除法的运算及意义;
由实数的运算法则来研究复数的运算规律。
教学目标
复数代数形式的加、减、乘、除的运算法则、运算律,以及复数加、减运算的几何意义
复数减法、除法的运算法则
教学重点
教学难点
复数的四则运算
复数的加法
我们规定,复数的加法法则如下设z1=a+bi,z2=c+di(a,b,c,d∈R)是任意两个复数,那么它们的和
(a+bi)+(c+di)=(a+c)+(b+d)
很明显,两个复数的和仍然是一个确定的复数特别地,当z1,x2都是实数时,把它们看作复数时的和就是这两个实数的和
复数的四则运算
复数的加法满足交换律、结合律吗?
容易得到,对任意z1,z2,z3∈C,有
z1+z2=z2+z1,
(z1+z2)+z3=z1+(z2+z3)
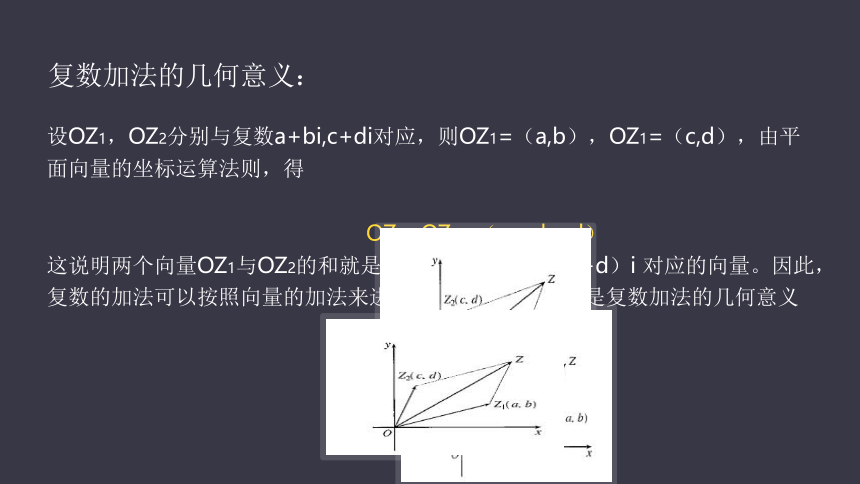
复数加法的几何意义:
设OZ1,OZ2分别与复数a+bi,c+di对应,则OZ1=(a,b),OZ1=(c,d),由平面向量的坐标运算法则,得
OZ1+OZ2=(a+c,b=d)
这说明两个向量OZ1与OZ2的和就是与复数(a+c)+(b+d)i 对应的向量。因此,复数的加法可以按照向量的加法来进行(如下图),这就是复数加法的几何意义
2.复数的减法
我们知道,实数的减法是加法的逆运算,类比实数减法的意义,你认为该如何定义复数的减法?
这就是复数的减法法则。由此可见,两个复数的差是一个确定的复数。可以看出,两个复数相减,类似于两个多项式相减
(a+bi)-(c+di)=(a-c)+(b-d)i
复数减法的几何意义:
类比复数加法的几何意义,你得出复数减法的几何意义吗?
复数的减法相当于复平面上的向量相减,所得新的向量对应复数即为减法后的结果。
根据复数及其运算的几何意义,求复平面内的两点Z1(x1,y1),Z2(x2,y2)之间的距离
解:因为复平面内的点Z1(x1,y1),Z2(x2,y2)对应的复数分 别为z1=x1+y1i, z2=x2+y2i,所以点Z1,Z2之间的距离 |Z1Z2|=|Z1Z2|=|z2-z1|=|(x2+y2i)-(x1+y1i)|
=|(x2-x1)+(y2-y1)i|
=
1.计算
(1)(2+4i)+(3-4i);
(2) 5-(3+2i);
(3)(-3 - 4i)+(2+i)-(1-5i)
(4)(2-i)-(2+3i)+4i
1.(1)5; (2)2-2i; (3)-2+2i (4)0.
2.如图,向量OZ 对应的复数是z,分别作出下列运算的结果对应的向量:(1)z+1; (2)z-i; (3)z+(-2+i)
解: 由图可知点Z坐标为(-2,3),所以复数x=-2+3i
(1)z+1=-2+3i+1=-1+3i
综上所述,结论是:-1+3i
(2)z-i=-2+3i-1=-2+2i
综上所述,结论是:-2+2i
(1)z+(-2+i)=-2+3i-2+i=-4+4i
综上所述,结论是:-4+4i
3.证明复数的加法满足交换律、结合律
设: z1=a1+b1i, z2=a2+b2i, z3=a3+b1i.
(1) 因为
z1+ z2=(a1+b1i)+(a2+b2i)
=(a1+a2)+(b1+b2)i,
z2+ z1=(a2+b2i)+(a1+b1i)
=(a2+a1)+(b2+b1)i
又因为a1+a2=a2+a1,b1+b2=b2+b1,所以
z1+ z2=z2+ z1
(2)因为 (z1+z2)+z3 =[(a1+b1i)+(a2+b2i)]+(a3+b3i)
=[(a1+a2)+(b1+b2)i]+(a3+b3i)
=[(a1+a2)+a3]+[(b1+b2)+b3]i,
z1+(z2+z1) =(a1+b1i)+[(a2+b2i)+(a3+b3i)]
=(a1+b1i)+[(a2+a3)+(b2+b3)i
= [a1+(a2+a3)]+[b1+(b2+b3)]i.
又因为(a1+a2)+a1=a1+(a2+a3),(b1+b2)+b3=b1+(b2+b3),所以
(z1+z2)+z3=z1+(z2+z3).
3.证明复数的加法满足交换律、结合律
4,求复平面内下列两个复数对应的两点之间的距离:(1)z1=2+i, z2=3-i; (2)z3=8+5i,z4=4+2i
解:
(1) ∵ z1=2+i,z2=3-i,
∴ z1-z2=(2+i)-(3-i)=-1+2i,
∴ z1,z2对应的两点之间的距离为:
|z1-z2|=|-1+2i|= =
(2) ∵ z3=8+5i,z4=4+2i,
∴ z3-z4=8+5i-(4-2i)=4+3i,
∴ z3,z4对应的两点之间的距离为:
|z3-z4|=|4+3i|= =5
3.复数的乘法
设z1=a+bi, z2=c+di(a,b,c,d∈R)是任意两个复数,那么它们的积
(a+bi)(c+di)=ac+bci+adi+bd
=(ac-bd)+(ad+bc )i.
很明显,两个复数的积是一个确定的复数。特别地,当z1,z2都是实数时,把它们看作复数时的积就是这两个实数的积
复数的四则运算
复数的乘法满足交换律,结合律,对加法满足分配律
容易得到,对于任意z1,z2,z3∈C,有
z1z2 = z2z1,
(z1z2)z3 = z1(z2z3),
z1(z2+z3) =z1z2+z1z3.
计算 (1-2i)(3+4i)(-2+i).
解:
(1-2i)(3+4i)(-2+i)
=(11-2i)(-2+i)
=-20+15i
计算:(1)(2+3i)(2-3i); (2)
解:(1)(2+3i)(2-3i)
=22-(3i)
=4-(-9)
=13
(2) = 1+2i+
=1+2i-1
=2i
4.复数的除法
复数除法的法则是 (a+bi)÷(c+di)= + i(a,b,c,d∈R,且c+di≠0)。由此可见,两个复数相除(除数不为0),所得的商是一个确定的复数.
在进行复数除法运算时,通常先把(a+bi)÷(c+di)写成 的形式,再把分子与分母都乘分母的共轭复数c-di,化简后就可得到上面的结果。这里分子分母都乘分母的“实数化因式”(共轭复数),从而使分母“实数化”
计算 (1+2i)÷(3-4i).
解:
(1+2i)÷(3-4i)=
= =
= =
在复数范围内解下列方程: (1) +2=0
(2)a +bx+c=0,其中a,b,c∈R,且a≠0,△= -4ac<0
解:(1)因为( =(- =-2,所以方程 +2=0的根为 x=±
(2)将方程a +bx+c=0的二次项系数化为1,得
配方,得 即
由△<0,知 类似(1), 可得
所以原方程的根为
在复数范围内,实系数一元二次方程a +bx+c=0(a≠0)的求根公式为
(1)当Δ≥0时,
(2)当Δ<0时,
复数的四则运算
1.计算:
(1)(7-6i)(-3i);
(2)(3+4i)(-2-3i);
(3)(1+2i)(3-4i)(-2-i)
(1)-18-21i ; (2)6-17i; (3)-20-15i.
2.计算:
(1)( + i)(- + i);
(2) ;
(3) i(2-i)(1-2i)
答案:(1)-5 (2)-2i (3)5
3.计算
(1) (2)
(3) (4)
答案:(1)i; (2)-i ; (3)1-i; (4)-1-3i
4.在复数范围内解下列方程 (1) 9 +16=0;(2) +x+1=0.
解:
(1) ∵ 9 +16=0, =
∴ x=
(2) ∵ +x+1=0 ,
∴ ,
∴ , ∴
已知复数 z 满足 (其中i为虚数单位,则 =( )
A. B . C. D.
|
|
解:∵ , |z| = ,|z|=2,
则 =
故选:B.
∴
|
|
设复数z=a+bi(a,b ∈R),若 ,则z=( )
A. B. C. D.
C
解:
故选:C
∵
∴
∴
复数 的虚部是( )
A. i B. -i C. 1 D. -1
解:
则复数 的虚部是 1
故选:C
C
已知 ,则 = ( )
A. B. C. 2 D.
|z-2i|
解:由 =
得 =|2i|=2
故选:C
|z-2i|
C
总结
复数的四则运算
复数的加法
复数的减法
复数的乘法
复数的除法
总结
复数的四则运算
掌握复数代数形式的加法、减法、乘法和除法的运算及意义;
由实数的运算法则来研究复数的运算规律。
教学目标
复数代数形式的加、减、乘、除的运算法则、运算律,以及复数加、减运算的几何意义
复数减法、除法的运算法则
教学重点
教学难点
复数的四则运算
复数的加法
我们规定,复数的加法法则如下设z1=a+bi,z2=c+di(a,b,c,d∈R)是任意两个复数,那么它们的和
(a+bi)+(c+di)=(a+c)+(b+d)
很明显,两个复数的和仍然是一个确定的复数特别地,当z1,x2都是实数时,把它们看作复数时的和就是这两个实数的和
复数的四则运算
复数的加法满足交换律、结合律吗?
容易得到,对任意z1,z2,z3∈C,有
z1+z2=z2+z1,
(z1+z2)+z3=z1+(z2+z3)
复数加法的几何意义:
设OZ1,OZ2分别与复数a+bi,c+di对应,则OZ1=(a,b),OZ1=(c,d),由平面向量的坐标运算法则,得
OZ1+OZ2=(a+c,b=d)
这说明两个向量OZ1与OZ2的和就是与复数(a+c)+(b+d)i 对应的向量。因此,复数的加法可以按照向量的加法来进行(如下图),这就是复数加法的几何意义
2.复数的减法
我们知道,实数的减法是加法的逆运算,类比实数减法的意义,你认为该如何定义复数的减法?
这就是复数的减法法则。由此可见,两个复数的差是一个确定的复数。可以看出,两个复数相减,类似于两个多项式相减
(a+bi)-(c+di)=(a-c)+(b-d)i
复数减法的几何意义:
类比复数加法的几何意义,你得出复数减法的几何意义吗?
复数的减法相当于复平面上的向量相减,所得新的向量对应复数即为减法后的结果。
根据复数及其运算的几何意义,求复平面内的两点Z1(x1,y1),Z2(x2,y2)之间的距离
解:因为复平面内的点Z1(x1,y1),Z2(x2,y2)对应的复数分 别为z1=x1+y1i, z2=x2+y2i,所以点Z1,Z2之间的距离 |Z1Z2|=|Z1Z2|=|z2-z1|=|(x2+y2i)-(x1+y1i)|
=|(x2-x1)+(y2-y1)i|
=
1.计算
(1)(2+4i)+(3-4i);
(2) 5-(3+2i);
(3)(-3 - 4i)+(2+i)-(1-5i)
(4)(2-i)-(2+3i)+4i
1.(1)5; (2)2-2i; (3)-2+2i (4)0.
2.如图,向量OZ 对应的复数是z,分别作出下列运算的结果对应的向量:(1)z+1; (2)z-i; (3)z+(-2+i)
解: 由图可知点Z坐标为(-2,3),所以复数x=-2+3i
(1)z+1=-2+3i+1=-1+3i
综上所述,结论是:-1+3i
(2)z-i=-2+3i-1=-2+2i
综上所述,结论是:-2+2i
(1)z+(-2+i)=-2+3i-2+i=-4+4i
综上所述,结论是:-4+4i
3.证明复数的加法满足交换律、结合律
设: z1=a1+b1i, z2=a2+b2i, z3=a3+b1i.
(1) 因为
z1+ z2=(a1+b1i)+(a2+b2i)
=(a1+a2)+(b1+b2)i,
z2+ z1=(a2+b2i)+(a1+b1i)
=(a2+a1)+(b2+b1)i
又因为a1+a2=a2+a1,b1+b2=b2+b1,所以
z1+ z2=z2+ z1
(2)因为 (z1+z2)+z3 =[(a1+b1i)+(a2+b2i)]+(a3+b3i)
=[(a1+a2)+(b1+b2)i]+(a3+b3i)
=[(a1+a2)+a3]+[(b1+b2)+b3]i,
z1+(z2+z1) =(a1+b1i)+[(a2+b2i)+(a3+b3i)]
=(a1+b1i)+[(a2+a3)+(b2+b3)i
= [a1+(a2+a3)]+[b1+(b2+b3)]i.
又因为(a1+a2)+a1=a1+(a2+a3),(b1+b2)+b3=b1+(b2+b3),所以
(z1+z2)+z3=z1+(z2+z3).
3.证明复数的加法满足交换律、结合律
4,求复平面内下列两个复数对应的两点之间的距离:(1)z1=2+i, z2=3-i; (2)z3=8+5i,z4=4+2i
解:
(1) ∵ z1=2+i,z2=3-i,
∴ z1-z2=(2+i)-(3-i)=-1+2i,
∴ z1,z2对应的两点之间的距离为:
|z1-z2|=|-1+2i|= =
(2) ∵ z3=8+5i,z4=4+2i,
∴ z3-z4=8+5i-(4-2i)=4+3i,
∴ z3,z4对应的两点之间的距离为:
|z3-z4|=|4+3i|= =5
3.复数的乘法
设z1=a+bi, z2=c+di(a,b,c,d∈R)是任意两个复数,那么它们的积
(a+bi)(c+di)=ac+bci+adi+bd
=(ac-bd)+(ad+bc )i.
很明显,两个复数的积是一个确定的复数。特别地,当z1,z2都是实数时,把它们看作复数时的积就是这两个实数的积
复数的四则运算
复数的乘法满足交换律,结合律,对加法满足分配律
容易得到,对于任意z1,z2,z3∈C,有
z1z2 = z2z1,
(z1z2)z3 = z1(z2z3),
z1(z2+z3) =z1z2+z1z3.
计算 (1-2i)(3+4i)(-2+i).
解:
(1-2i)(3+4i)(-2+i)
=(11-2i)(-2+i)
=-20+15i
计算:(1)(2+3i)(2-3i); (2)
解:(1)(2+3i)(2-3i)
=22-(3i)
=4-(-9)
=13
(2) = 1+2i+
=1+2i-1
=2i
4.复数的除法
复数除法的法则是 (a+bi)÷(c+di)= + i(a,b,c,d∈R,且c+di≠0)。由此可见,两个复数相除(除数不为0),所得的商是一个确定的复数.
在进行复数除法运算时,通常先把(a+bi)÷(c+di)写成 的形式,再把分子与分母都乘分母的共轭复数c-di,化简后就可得到上面的结果。这里分子分母都乘分母的“实数化因式”(共轭复数),从而使分母“实数化”
计算 (1+2i)÷(3-4i).
解:
(1+2i)÷(3-4i)=
= =
= =
在复数范围内解下列方程: (1) +2=0
(2)a +bx+c=0,其中a,b,c∈R,且a≠0,△= -4ac<0
解:(1)因为( =(- =-2,所以方程 +2=0的根为 x=±
(2)将方程a +bx+c=0的二次项系数化为1,得
配方,得 即
由△<0,知 类似(1), 可得
所以原方程的根为
在复数范围内,实系数一元二次方程a +bx+c=0(a≠0)的求根公式为
(1)当Δ≥0时,
(2)当Δ<0时,
复数的四则运算
1.计算:
(1)(7-6i)(-3i);
(2)(3+4i)(-2-3i);
(3)(1+2i)(3-4i)(-2-i)
(1)-18-21i ; (2)6-17i; (3)-20-15i.
2.计算:
(1)( + i)(- + i);
(2) ;
(3) i(2-i)(1-2i)
答案:(1)-5 (2)-2i (3)5
3.计算
(1) (2)
(3) (4)
答案:(1)i; (2)-i ; (3)1-i; (4)-1-3i
4.在复数范围内解下列方程 (1) 9 +16=0;(2) +x+1=0.
解:
(1) ∵ 9 +16=0, =
∴ x=
(2) ∵ +x+1=0 ,
∴ ,
∴ , ∴
已知复数 z 满足 (其中i为虚数单位,则 =( )
A. B . C. D.
|
|
解:∵ , |z| = ,|z|=2,
则 =
故选:B.
∴
|
|
设复数z=a+bi(a,b ∈R),若 ,则z=( )
A. B. C. D.
C
解:
故选:C
∵
∴
∴
复数 的虚部是( )
A. i B. -i C. 1 D. -1
解:
则复数 的虚部是 1
故选:C
C
已知 ,则 = ( )
A. B. C. 2 D.
|z-2i|
解:由 =
得 =|2i|=2
故选:C
|z-2i|
C
总结
复数的四则运算
复数的加法
复数的减法
复数的乘法
复数的除法
总结
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
