8.6 空间直线、平面的垂直 课件(111张PPT)
文档属性
| 名称 | 8.6 空间直线、平面的垂直 课件(111张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 7.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-21 23:57:40 | ||
图片预览











文档简介
(共111张PPT)
空间直线、平面的垂直
教学目标
异面直线所成角、直线与平面所成角、二面角的定义;
直线与直线、直线与平面、平面与平面垂直的判定定理,异面
直线所成角、直线和平面所成的角、二面角及其求法;
异面直线垂直、直线与平面垂直、平面与平面垂直的判定定理
的综合应用.
教学重点
教学难点
异面直线所成的角、直线与平面所成的角、二面角的求解;
异面直线垂直、直线与平面垂直、平面与平面垂直的判定.
找异面直线所成的角、直线与平面所成的角、二面角;
异面直线垂直、直线与平面垂直、平面与平面垂直的判定定
理的应用.
引入
空间中两条直线的位置关系
1.空间两条直线的位置关系有三种:__________、_________、_________.
异面直线
平行直线
相交直线
2.分类
(1)从有无公共点的角度来看,可分为两类
平行直线
无公共点
(2)从是否共面的角度来看,可分为两类
相交直线
共面直线
直线
平行直线
不共面直线:异面直线
有且仅有一个公共点:相交直线
直线
异面直线
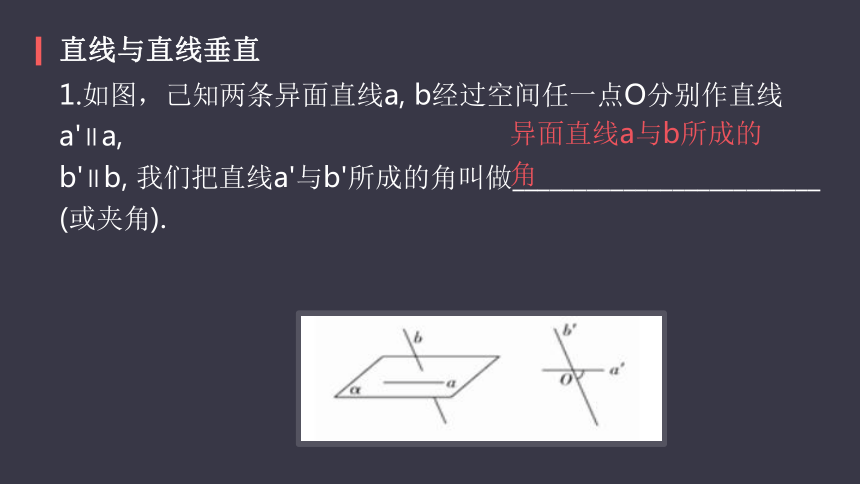
直线与直线垂直
异面直线a与b所成的角
1.如图,己知两条异面直线a, b经过空间任一点O分别作直线a'∥a,
b'∥b, 我们把直线a'与b'所成的角叫做_________________________
(或夹角).
0°≤a≤90°
2.范围:______________.
3.当θ=____时,a与b互相垂直,记作______.
异面直线所成角的范围是0°<θ≤90°,所以垂直有两种情况:
异面垂直和相交垂直.
4.当两条直线a,b相互平行时,我们规定它们所成的角为________.
所以空间两条直线所成角α的取值范围是________________.
0°<θ≤90°
a⊥b
90°
0°
[教材解难]
求异面直线所成的角的步骤
(1)找出(或作出)适合题设的角——用平移法, 遇题设中有中点,
常考虑中位线;若异面直线依附于某几何体,且对异面直线平移
有困难时,可利用该几何体的特殊点,使异面直线转化为相交
直线.
(2)求——转化为一个三角形的内角,通过解三角形,求出所找的
角.
(3)结论——设由(2)所求得的角的大小为θ. 若0°<θ≤90°,则θ为
所求;若90°<θ≤180°,则180°- θ为所求.
例1如图8.6-3, 已知正方体ABCD-A'B'C'D'.
(1)哪些棱所在的直线与直线 AA'垂直?
(2)求直线BA'与CC'所成的角的大小.
(3)求直线BA'与AC所成的角的大小.
解: (1)棱AB, BC, CD, DA, A'B', B'C', C'D', D'A'所在直线分别与直线AA'垂直.
(2)因为ABCD-A'B'C'D'是正方体,所以BB'∥CC, 因此∠A'BB'为直线BA'与
CC'所成的角. 又因为∠A'BB'=45°, 所以直线BA'与CC所成的角等于45°.
(3)如图8.6-4,连接A'C', 因为ABCD-A'B'C'D'是正方体,所以AA'⊥CC'.从
而四边形AA'C'C是平行四边形,所以AC//A'C.于是∠BA'C'为异面直线
BA'与AC所成的角,
连接BC',易知△A'BC'是等边三角形,所以∠BA'C'=60°.从而异面直线BA'
与AC所成的角等于60°.
例 在正方体 ABCD-A1B1C1D1中,E, F分别是A1B1, B1C1的中点,
求异面直线DB1与EF所成的角的大小.
拓展练习
[解] 方法一 如图所示, 连接A1C1, B1D1, 并设它们相交于点O,
取DD1的中点G, 连接OG, A1G, C1G,
则OG// B1D,EF//A1C1,
∴∠GOA1为异面直线DB1与EF所成的角(或其补角)
∵GA1=GC1, O为A1C1的中点,∴GO⊥A1C1.
∴异面直线DB1与EF所成的角为90°.
方法二 如图所示,连接A1D, 取A1D的中点H, 连接HE,则HE∥
∴∠HEF为异面直线DB1与EF所成的角(或其补角).
方法三:如图,连接A1C1, 分别取AA1, CC1的中点M, N,连接MN.
∵E, F分别是A1B1, B1C1的中点,
∴EF//A1C1, 又MN// A1C1, ∴MN// EF.
连接DM, B1N, MB1, DN, 则B1N//DM,
∴四边形DMB1N为平行四边形,∴MN与DB1必相交,
设交点为P,则∠DPM 为异面直线DB1与EF所成的角(或其补角).
方法四: 如图,在原正方体的右侧补上一个与其大小相等的正方体,
连接B1Q,易得B1Q// EF,
∴∠DB1Q就是异面直线DB1与EF所成的角(或其补角).
方法归纳
求异面直线所成角的步骤
一作: 选择适当的点,用平移法作出异面直线所成的角;
二证: 证明作出的角就是要求的角;
三计算: 将异面直线所成的角放入某个三角形中,利用特殊三角形
求解.
例2如图,在正方体ABCD-A1B1C1D1中,O1为底面A1B1C1D1的中心,
求证AO1⊥BD.
[证明] 如图,连接B1D1
∵ABCD-A1B1C1D1是正方体, ∴BB1∥DD1.
∴四边形BB1D1D是平行四边形, ∴B1D1// BD.
∴直线AO1与B1D1所成的角即为直线AO1与BD所成
的角. 连接AB1, AD1, 易证AB1=AD1.
又O1为底面A1B1C1D1的中心, ∴O1为B1D1的中点
∴AO1⊥B1D1, ∴AO1⊥BD.
方法归纳
证明直线与直线垂直的方法
①等腰三角形中线即是高线.
②勾股定理.
③异面直线所成的角为直角.
证明: 如图,取AC的中点F, 连接DF, EF,
在△PAC中,∵D是PC的中点,F是AC的中点,
∴DF//PA, 同理可得EF// BC,
∴∠DFE为异面直线PA与BC所成的角(或其补角).
在△DEF中,DE=3,
1.判所下列命题是否正确, 正确的在括号内画"√".错误的画“×".
(1)如果两条平行直线中的一条与已知直线垂直,那么另一条也
与已知直线垂直. ( )
(2)垂直于同一条直线的两条直线平行 ( )
2.如图, 在长方体ABCD-A'B'C'D'的各条棱所在直线中.
(1)与直线AB垂直的直线有____条;
(2)与直线AB异面且垂直的直线有____条;
(3)与直线AB和A'D'都垂直的直线有____条;
(4)与直线AB和A'D'都垂直且相交的直线是______.
8
4
4
1
(1)直线BC和AC'所成的角的大小:
(2)直线AA'和BC"所成的角的大小.
(1)因为BC∥BC ,所以∠B'C'A'是异面直线A'C'与BC所成的角
4.如图. 在正三棱柱ABC-A'B'C'中. D为棱AC的中点. AB=BB'=2.
求证BD⊥AC'.
引入
定义
画法
直线与平面垂直
如果直线l与平面α内的__________直线都______,就说
直线l与平面α互相垂直,记作.直线_____. 直线l叫作平
面α的_____,平面α叫作直线l的_____,直线与平面垂
直时,它们唯一的公共点P叫作______.
任意一条
垂直
l⊥a
垂线
垂面
垂足
通常把直线画成与表示平面的平行四边形的一边垂直,
如图
PO为垂线段,其长度为点P到面α的距离
垂线段
过一点垂直于已知平面的直线有且只有一条
文字语言: 如果一条直线与一个平面内的_____________________,
则该直线与此平面垂直.
直线与平面垂直的判定定理
两条相交直线垂直
图形语言:如图所示.
1.直线与平面垂直是直线与平面相交的特殊情形.
2.注意定义中“任意一条直线”与“所有直线”等同但不可说成“无数
条直线”.
3.判定定理条件中的“两条相交直线”是关键性词语,此处强调“相
交”,若两条直线平行,则直线与平面不一定垂直.
证明: 如图8.6-13,在平面α内取两条相交直线m, n,
∴直线a⊥α, ∴a⊥m, a⊥n.
∵b//a, ∴b⊥m, b⊥n.
又m α, n α, m,n是两条相交直线,
∴b⊥α.
例3 求证:如果两条平行直线中的一条直线垂直于一个平面,那
么另一条直线也垂直于这个平面.
已知: 如图8.6-12, a//b, a⊥α, 求证b⊥α.
例 如图所示, 已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC, AC=BC, N是AB的中点.求证: CN⊥平面ABB1A1.
AA1⊥底面ABC
CN 底面ABC
AA1⊥CN
AC=BC
N是AB的中点
AB⊥CN ,
又AA1 平面ABB1A1, AB 平面ABB1A1, AA1∩AB=A,所以
CN⊥平面ABB1A1.
证明
方法归纳
线面垂直的判定定理实质是由线线垂直推证线面垂直,途径是找到
一条直线与平面内的两条相交直线垂直. 推证线线垂直时注意分析
几何图形,寻找隐含条件.
直线与平面所成的角
直线和平面所成的角
当直线与平面垂直时,它们所成的角是90°.当直线与平面
平行或在平面内时,它们所成的角是___.
定义
范围
画法
平面的一条斜线和它在平面上的_____所成的___,叫作这
条直线和这个平面所成的角.
射影
角
0°
如图,______就是斜线AP与平面α所成的角
0°≤θ≤90°
∠PAO
把握定义应注意两点: ①斜线上不同于斜足的点P 的选取是任意的;
②斜线在平面上的射影是过斜足和垂足的一条直线而不是线段.
例4 如图,在正方体ABCD-A1B1C1D1中, 求直线A1B和平面
A1DCB1所成的角.
解 连接BC1, BC1与B1C相交于点O, 连接A1O.
设正方体的棱长为a.
∵A1B1⊥B1C1, A1B1⊥B1B, B1C1∩B1B=B1,
∴A1B1⊥平面BCC1B1. ∴A1B1⊥BC1.
又BC1⊥B1C, ∴BC1⊥平面A1DCB1.
方法归纳
求直线与平面所成的角的步骤
(1)作: 在斜线上选取恰当的点向平面引垂线,在这一步确定垂足的
位置是关键;
(2)证: 证明所找到的角为直线与平面所成的角,证明的主要依据为
直线与平面所成的角的定义;
(3)求: 一般来说是借助三角形的相关知识求角.
1.如果两条直线和一个平面所成的角相等,那么这两条直线一定
平行吗
两条直线与一个平面所成的角相等,则这两条直线相交、平行
或异面,例如圆锥的两条母线,与底面所成角相等,但是母线
是相交直线.
2.如图. 四梭锥S-ABCD的底面是正方形. SD⊥平面ABCD. 求证:
AC⊥平面SDB.
解答 ∵四棱柱A1B1C1D1-ABCD是直棱柱,
∴B1D1⊥A1A, 若A1C⊥B1D1
则B1D1⊥平面A1AC1C
∴B1D1⊥AC,
又由B1D∥BD,
则有BD⊥AC,
反之,由BD⊥AC亦可得到A1C⊥B1D1
故答案为: BD⊥AC.
3.如图,在直四棱柱A'B'C'D'-ABCD中,当底面四边形ABCD满
足什么条件时,A'C⊥B'D'? .
4. 过△ABC所在平面α外一点P. 作PO⊥α, 垂足为O. 连接PA, PB,
PC.
(1)若PA=PB=PC, 则点O是△ABC的___心.
(2)若PA=PB=PC, ∠C=90°, 则点O是AB边的___点
(3)若PA⊥PB, PB⊥PC, PC⊥PA, 垂足都为P.则点O是△ABC的___
心.
外
中
垂
直线与平面垂直的性质
①线面垂直→线线平行;
②作平行线
文字语言
垂直于同一个平面的两条直线_____
平行
符号语言
图形语言
作用
a//b
a⊥α
b⊥α
→_____
1.直线与平面垂直的性质定理给出了判定两条直线平行的另一种方
法.
2.定理揭示了空间中“平行”与“垂直”关系的内在联系,提供了
“垂直”与“平行”关系转化的依据.
例5 如图8.6-19, 直线l平行于平面α, 求证: 直线l上各点到平面
α的距离相等.
证明:过直线l上任意两点A, B分别作平面α的垂线AA1, BB1,
垂足分别为A1, B.
∵AA1⊥α, BB⊥α.
∴AA1//AB1
设直线AA1, BB1确定的平面为β. β∩α= A1B1
∵l//α
∴l//A1B1
∴四边形AA1B1B是矩形,
∴AA1= BB1.
由A, B是直线l上任取的两点. 可知直线l上各点到平面α的距离相等.
一条直线与一个平面平行时,这条直线上任意一点到这个平面的距
离,叫做这条直线到这个平面的距离. 由例5我们还可以进一步得出,
如果两个平面平行,那么其中一个平面内的任意一点到另一个平面
的距离都相等. 我们把它叫做这两个平行平面间的距离.
例6 推导棱台的体积公式
其中S',S分别是棱台的上、下底面面积,h是高.
解: 如图8.6-20. 延长棱台各侧棱交于点P. 得到截得棱台的
棱锥. 过点P作棱台的下底面的垂线,分别与梭台的上、下
底面交于点O', 则PO垂直于棱台的上底面(想一想,为什么
?). 从而O'O=h.
设藏得棱台的棱锥的体积为V, 去掉的棱锥的体积为V'、高为h', 则PO'=h'.
于是
由棱台的上、下底面平行. 可以证明棱台的上、下底面相似, 所以
例在正方体ABCD-A1B1C1D1中,点E, F分别在A1D, AC上,
EF⊥A1D, EF⊥AC, 求证: EF//BD1.
[证明]如图所示, 连接A1C1, C1D, B1D1, BD.
∵AC//A1C1, EF⊥AC, ∴EF⊥A1C1.
又EF⊥A1D, A1D∩AC1=A1, ∴EF⊥平面A1C1D1 ①
∵BB1⊥平面A1B1C1D1, A1C1 平面A1B1C1D1,
∴BB1⊥A1C1
∵四边形A1B1C1D1为正方形, ∴A1C1⊥B1D1,
又B1D1∩BB1=B1, ∴A1C1⊥平面BB1D1D,
而BD1 平面BB1D1D, ∴A1C1⊥BD1. 同理DC1⊥BD1.
又DC1∩A1C1=C1, ∴BD1⊥平面A1C1D. ②
由①②可知EF// BD1.
方法归纳
线面垂直的性质定理是证明两直线平行的重要依据,证明两直线平
行的常用方法:
(1)a//b, b//c→a//c.
(2)a//α, a β, β∩α=b→a// b.
(3)α//β, γ∩α=a, γ∩β=b→a//b.
(4)a⊥α, b⊥α→a//b.
1.已知直线a, b和平面α, 且a⊥b, a⊥α, 则b与a的位置关系是
_______.
a//b
2.已知A, B两点在平面α的同侧,且它们与α的距离相等,求证:
直线AB//α.
证明: 作出点A、B到α的垂线段AA'、BB'.
AA'平行且等于BB'→AA'BB'是平行四边形
→AB//A'B', AB α,A'B' α→AB//α.
3.如图,EA和DC都垂直于平面ABC, 且EA=2DC, F是EB的中点,
求证: DF //平面ABC.
∴FG∥CD,FG=CD,
∵FG⊥平面ABC,
∴四边形CDFG是矩形,DF∥CG,
CG 平面ABC,DF不包含于平面ABC,
∴DF∥平面ABC.
4.求证: 垂直于同一条直线的两个平面互相平行. (提示:过这条直
线作平面与这两个平面相交,则它们的交线平行.)
证明:设直线为l,平面为α,β.
而l⊥α,l⊥β. 则过l作平面m,
且l 平面m, 则
假设m∩α=l1, m∩β=l2.
由提示 l1∥l2,
又l1 α, l2 α,则l2∥α.
同理过l作平面n,使n∩α=l3, n∩β=l4.
则同理l4∥平面α.
又l3 β,l4 β,则α∥β.
二面角
图示
平面内的一条直线把平面分成两部分,这两部分通常称
为_______. 从这一条直线出发的____________所组成的图
形叫做二面角. 这条直线叫做二面角的___, 这两个半平
面叫做二面角的___.
概念
半平面
两个半平面
棱
面
平
面
角
OA α,OB β, α∩β=l, O∈l, OA⊥l, OB⊥l→∠AOB
是二面角的平面角.
文字
图示
符号
范围
规定
在二面角的棱上任取一点,以该点为垂足,在两个半平面内
分别作垂直于___的射线,则这两条射线构成的___叫做这个
二面角的平面角
棱
角
二面角的大小可以用它的________来度量, 二面角的平面角是多
___________________
0°≤∠AOB≤180°
少度,就说这个二面角是多少度, 平面角是_____ 的二面角叫做
直二面角
直角
平面角
棱为l,面分别为α, β的二面角记为_________ . 如图所示,
也可在α, β内(棱以外的半平面部分)分别取点P, Q, 将这个
二面角记作二面角__________.
记法
a-1- β
P-l-Q
无关如图,根据等角定理可知,∠AOB=∠A'O'B', 即二面角的平面
角的大小与角的顶点的位置无关,只与二面角的大小有关.
1.二面角与平面几何中的角有什么区别
平面几何中的角是从一点出发的两条射线组成的图形; 二面角是从
一条直线出发的两个半平面所组成的图形.
2.二面角的平面角的大小,与角的顶点在棱上的位置有关吗
例 下列命题中:
①两个相交平面组成的图形叫做二面角; ②异面直线a, b分别和一
个二面角的两个面垂直,则a, b所成的角与这个二面角的平面角
相等或互补; ③二面角的平面角是从棱上一点出发,分别在两个
面内作射线所成的角的最小角; ④二面角的大小与其平面角的
顶点在棱上的位置没有关系.其中正确的是 ( ) A.①③ B.②④ C.③④ D.①②
拓展练习
解析 由二面角的定义: 从一条直线出发的两个半平面所组成的图形
叫做二面角, 所以①不对,实质上它共有四个二面角; 由a,b分别垂
直于两个面,则a, b都垂直于二面角的棱,故②正确; ③中所作的
射线不一定垂直于二面角的棱,故③不对; 由定义知④正确. 故选B.
答案B
规律方法
1.要注意区别二面角与两相交平面所成的角并不一致.
2.要注意二面角的平面角与顶点在棱上且角两边分别在二面角面
内的角的联系与区别.
3.可利用实物模型,作图帮助判断.
1. 定义: 两个平面相交,如果它们所成的二面角是___________, 就
说这两个平面互相垂直. 平面α与平面β垂直,记作________.
2.画法: 两个互相垂直的平面通常把直立平面的竖边画成与水平平
面的______垂直.如图所示.
平面与平面垂直
直二面角
α⊥β
横边
平面与平面垂直的判定定理
l⊥α, ______ →α⊥β
文字语言
图形语言
符号语言
一个平面过另一个平面的_______,则这两个平面
垂直
垂线
l β
例7如图 8.6-27所示,在正方体ABCD-A'B'C'D'中,求证: 平面
A'BD⊥平面ACC'A'.
证明: ∵ABCD-A'B'C'D'是正方体,
∴AA⊥平面ABCD.
∴AA'⊥ BD.
又BD⊥AC.
∴BD⊥平面ACC'A'.
∴平而A'BD⊥平面ACC'A'.
例8如图8.6-28. AB是⊙O的直径, PA垂直于⊙O所在的平面,
C是圆周上不同于A,B的任意一点. 求证: 平面PAC⊥平面PBC.
证明: ∵PA⊥平面ABC,
BC 平面ABC.
∴PA⊥BC.
∵点C是圆周上不同于A, B的任意一点, AB是⊙O的直
径,
∴∠BCA=90°, 即BC⊥AC.
又PA∩AC=A, PA 平面PAC, AC 平面PAC,
∴BC⊥平面PAC,
又BC 平面PBC,
∴平面PAC⊥平面PBC.
拓展练习
如图所示,AB是⊙O的直径,PA垂直于⊙O所在的平
面,C是圆周上的一点,且PA=AC, 求二面角P-BC-A
的大小
解 ∵PA⊥平面ABC, BC 平面ABС,
∴PA⊥ВС.
∵AB是⊙O的直径,且点C在圆周上,∴AC⊥BC.
又∵РА∩AC=А, ∴BC⊥平面PAC.
而PC 平面PAC, ∴PC⊥BC.
又∵BC是二面角P-BC-A的棱,
∴∠PCA是二面角P-BC-A的平面角.
由PA=AC知,△PAC是等腰直角三角形,
∴∠PCA=45°,即二面角P-BC-A的大小是45°.
规律方法 确定二面角的平面角的方法:
(1)定义法: 在二面角的棱上找一特殊点,在两个半平面内分别作垂
直于棱的射线.
(2)垂面法: 过棱上一点作棱的垂直平面,该平面与二面角的两个半
平面产生交线,这两条交线所成的角,即为二面角的平面角.
(3)线面垂直法: 该法就是利用线面垂直来寻找二面角的平面角,是
最常用的也是最好用的一种方法. 由一个半平面内异于棱上的点A向
另一半平面作垂线,垂足为点B, 由B点向二面角的棱作垂线,垂足
为点O, 连接AO, 则∠AOB为二面角的平面角(或其补角) .
空间中的垂直关系
1.如图。检查工作的相邻两个(平)面是否垂直时,只要用曲尺的
一边紧靠在工件的一个面上,另一边在工件的另一个面上转动,
观察尺边和这个面是否密合就可以了, 这是为什么
解答
检查工件的相邻的两个面是否垂直时,只要
用曲尺的一边紧靠在工件的一个面上,
另一边在工件的另一个面上转动一下,若曲尺的另一
边和工件的另一面密合, 就说明工件的另一个面经过
工件的一个面的垂线, 由面面垂直的判定定理得工件
的这两个互相垂直。 如果不转运,无法判断曲尺的
另一边和工件的另一面是否密合, 也就无法判断工件
的相邻的两个面是否垂直.
2.已知直线a, b与平面α, β, γ. 能使α⊥β的充分条件是( ).
(A)α⊥γ ,β⊥γ
(B)α∩β=a, b⊥a, b β
(C) a// , a//α
(D) a//α, a⊥β
D
3.如下页图. AB⊥平面BCD,BC⊥CD. 你能发现哪些平面互相
垂直,为什么?
解答 平面ABC⊥平面BCD, 平面ABD⊥平面BCD, 平面ACD⊥平
面ABC
4.如图,在正三棱柱ABC-A'B'C'中,D为棱AC的中点.求证: 平
面BDC'⊥平面ACC'A'.
证明: ∵ A'A⊥平面ABC
BD 平面ABC
∴A'A⊥BD
∵△ABC是正三角形, D为棱AC的中点
∴BD⊥AC
∵BD⊥A'A ,BD⊥AC,AA' 平面ACC'A,AC 平面ACC'A,
A'A∩AC=A→BD⊥平面ACC'A
又∵BD 平面BDC'
∴BDC'⊥平面ACC'A'
平面与平面垂直的性质定理
两个平面垂直,则一个平面内垂直于交线的直线与另
一个平面______
垂直
文字语言
符号语言
a⊥β
a∩β=l
a α
a⊥l
→a⊥β
图形语言
作用
证明直线与平面垂直
例9如图8. 6-32.已知平面α⊥平面β. 直线a⊥β, a α. 判断a与α的
位置关系.
解:在α内作垂直于α与β交线的直线b,
∵α⊥β.
∴b⊥β.
又a⊥β.
∴a//b.
又a α.
∴a//α.
即直线a与平面α平行.
例 如图8.6-33, 已知PA⊥平面ABC,平面PAB⊥平面PBC.
求证: BC⊥平面PAB.
证明:如图8.6-34,过点A作AE⊥PB, 垂足为E.
∵平面PAB⊥平面PBC,平面PAB∩平面PBC=PB,
∴AE⊥平面PBC,
∵BC 平面PBC,
∴AE⊥BC.
∵PA⊥平面ABC, BC 平面ABC,
∴PA⊥BC.
又PA∩AE=А,
∴BC⊥平面PAB.
拓展练习
如图所示, P是四边形ABCD所在平面外的一点,四边形ABCD是
∠DAB=60°的菱形,侧面PAD为正三角形, 其所在平面垂直于底面
ABCD. 若G为AD边的中点,求证:BG⊥平面PAD.
拓展练习
证明: 连接PG, BD,
∵四边形ABCD是菱形且∠DAB= 60°,
∴△ABD是正三角形,
∵G是AD的中点,
∴BG⊥AD.
又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴BG⊥平面PAD.
规律总结
1. 若所给题目中有面面垂直的条件,一般要利用面面垂直的定理
将其转化为线面垂直、线线垂直. 在应用面面垂直的性质定理时,注意三点: ①两个平面垂直,是前提条件; ②直线必须在其中一个
平面内; ③直线必须垂直于它们的交线.
2. 先找条件中有没有在一个平面内与交线垂直的直线,若没有与
交线垂直的直线,一般需作辅助线, 基本作法是过其中一个平面内
一点作交线的垂线, 这样便把面面垂直问题转化为线面垂直问题,
进而转化为线线垂直问题.
1. 判断下列命题是否正确,正确的在括号内画“√”,错误的画
“×”.
(1)如果平面α⊥平面β, 那么平面α内所有直线都垂直于平面β.
( )
(2)如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β.
( )
(3)如果平面α不垂直于平面β,那么平面a内一定不存在直线垂直
于平面β.
( )
2. 若平面α⊥平面β,且a∩β=l, 则下列命题中正确的个数是( )
(1)平面α内的直线必垂直于平面β内的任意一条直线.
(2)平面α内的已知直线必垂直于平面β内的无数条直线.
(3)平面α内的任一条直线必垂直于平面β.
(4)过平面α内任意一点作交线l的垂线,则此垂线必垂直于平面β.
(A) 3 (B) 2 (C) 1 (D) 0
B
3.已知α,β是两个不同的平面,m为平面α内的一条直线,则
“α⊥β”是“m⊥β”的( ).
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
B
解答
设过直线 a与平面α内的一点的平面与α的交线为a'.
∵a∥α, ∴a∥a'.
∵a⊥AB,
∴a'⊥AB.
∵a' α,α⊥β,
∴a'⊥β.
∴a⊥β, 即a与β的位置关系是a⊥β.
4. 已知平面α,β. 直线a, 且α⊥β,α∩β=AB. a//α, a⊥AB. 判断直
线a与平面β的位置关系. 并说明理由.
1.选择题
(1)若空间中四条不同的直线l1, l2, l3, l4满足l1⊥l2, l2⊥l3, l3⊥l4. 则下面
结论正确的是( ).
(A)l1⊥l4 (B)l1//l4
(C) l1, l4既不垂直也不平行 (D)l1, l4的位置关系不确定
(2) 设l, m, n均为直线. 其中m, n在平面α内. 则"l⊥α”是"l⊥m"且“l⊥n”
的( ).
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
(3)直线l1, l2互相平行的一个充分条件是( )
(A)l1, l2都平行于同一个平面 (B) l1, l2与同一个平面所成的角相等
(C) l1, l2都垂直于同一个平面 (D)l1平行于l2所在的平面
D
A
D
2.判断下列命题是个正确,正确的在括号内画"√",错误的画"X".
(1)过平面外一点,有且只有一条直线与这个平面垂直. ( )
(2)过平面外一点,有且只有一条直线与这个平面平行. ( )
(3)过直线外一点,有且只有一个平面与这条直线垂直. ( )
(4)过直线外一点,有且只有一个平面与这条直线平行. ( )
(5)过直线外一点,有且只有一条直线与这条直线平行. ( )
3.判断下列命题是否正确. 正确的说明理由, 错误的举例说明.
(1) 一条直线行于一个平面,另一条直线与这个平面垂直,则这两条
直线互相垂直;
(2)如果平面α//平面α1,平面β//平面β1,那么平面α与平面β所成的
二面角和平面α1与与平面β1所成的二面角相等或互补;
(3)如果平面α⊥平面β,平面β⊥平面γ,那么平而α⊥平面γ.
解: (1)正确, 设直线a//平面α , 直线b⊥平面α , 则存在直线c α,且a//c, ∴b⊥c, ∴b⊥a.
(2)正确, 两个平面平行, 则其法向量也平行, 两个二面角的两个半平
面的法向量所成角相等或互补;
(3)错误, 如长方体中两底面都与同一侧面垂直, 但两底面不垂直.
4. 如图, 在直二棱柱ABC-A1B1C1中, CA=CB, P为AB
的中点, Q为棱C1C的中点. 求证:
(1)PQ⊥AB; (2) PQ⊥C1C; (3) PQ⊥A1B.
证明: (1)如图, 取AB的中点D ,连接CD、DP,
∴PD//CQ , ∴四边形CDPQ为平行四边形, ∴CD//PQ.
又∵CACB , D为AB的中点,∴CD⊥AB,∴PQ⊥AB .
(2)在直三棱柱ABC-A1B1C1中, AA1⊥平面ABC, CD 平面ABC,
∴AA1⊥CD , 由(1)知CD//PQ, ∴PQ⊥AA1. 又AA1//CC1,∴PQ⊥CC1.
(3)由(1) (2)知, PQ⊥AB,PQ⊥AA1, 而AB∩AA1=A.
∴PQ⊥平面AA1B1B. ∵A1B 平面AA1B1B, ∴PQ⊥A1B .
5. 如图,在三棱锥P-ABC中,CD⊥AB,垂足为D,
PO⊥底面ABC, 垂足为O,且O在CD上, 求证AB⊥PC.
证明: ∵PO⊥底面ABC, AB 底面ABC, ∴PO⊥AB.
∵O在CD上,∴PO∩CD=O.
又CD⊥AB
∴AB⊥平面POC,∵PC 平面POC, ∴AB⊥PC.
6.如图,在正方体ABCD-A'B'C'D'中,平面ABC'D'与正方
体的各个面所在的平面所成的二面角的大小分别是多少?
解: 在正方体ABCD-A'B'C'D'中,考虑平面ABC'D'与平面ABCD ,
AB⊥平面B'C'CB , BC', BC 平面B'C'CB , 所以平面∠B'BC就是平面ABC'D'与
平面ABCD所成角, 即平面ABC'D'与平面ABCD成角∠C'BC=45°.
同理平面ABC'D'与平面ABCD, 平面A'B'C'D' , 平面ABB'A' , 平面CC'D'D都成
45°角,
又因为AB⊥平面ADD'A' , 平面ABC'D'与平面ADD'A'垂直, 即所成的角为90° ,
同理可得平面ABC'D'与平面ADD'A' , 平面BCC'B'都垂直, 即与它们所成的角为
90°.
所以平面ABC'D'与平面ABCD, 平面A'B'C'D' , 平面ABB'A' , 平面CC'D'D都成
45°角, 平面ABC'D'与平面ADD'A', 平面BCC'B'都垂直, 即与它们所成的角为90°.
7.如图,在三棱锥V-ABC中,已知∠VAB=∠VAC=
∠ABC=90°,判断平面VAB与平面VBC的位置关系,
并说明理由.
解答
∵∠VAB=∠VAC=90°, ∴ VA⊥AB, VA⊥AC, 又AB∩AC= A,
∴VA⊥平面ABC,∴VA⊥BC.
∠ABC=90° , ∴AB⊥BC , VA∩VB= V,
∴BC⊥平面VBA,又ВC 平面VBC,
∴平面VBA⊥平面VBC.
8. 求证:如果共点的三条直线两两垂直,那么它们中每两条直线确
定的平面也两两垂直.
解答
已知: 直线a,b,c共点且两两垂直,直线a和b确定的平面为α, 直
线a和c确定的平面为β, 直线b和c确定的平面为γ,
求证: a⊥γ,b⊥β,c⊥α,
证明: ∵直线a, b,c共点且两两垂直, 直线b和c确定的平面为γ,
∴由直线与平面垂直的判定定理可得a⊥γ,同理可证b⊥β,c⊥α,
∴原命题得证
解答
证明: 如图,
∵平面α⊥平面γ,
∴平面α与平面γ相交, 设交线为m ,
在平面α内作直线a⊥m, ∵平面α⊥平面γ,∴a⊥γ,
在平面β内任取一点O, 由直线a和点O确定平面M,设M∩β于b,
∵平面α∥平面β, 由面面平行的判定定理, 得a∥b,
∵a// b,a⊥γ, ∴b⊥γ
又∵b β,
∴平面β⊥平面γ.
9. 已知平面α, β, γ,且α⊥γ, β//α, 求证β⊥γ.
10. 已知平面α, β, γ, 且α⊥γ, β⊥γ, α∩β=l, 求证l⊥γ.
解答
证明: 如图, 在平面内γ任取一点P,
过点P作PA⊥l1, PB⊥l2,A,B为垂足.
∵α∩γ=l1,α⊥γ, PA γ, ∴PA⊥α
又∵l α, ∴PA⊥I.
同理: PB⊥l,
∴l⊥γ.
11. 如图,在正方体ABCD-A1B1C1D1中,点P, Q分别为棱AD, CC1
的中点, 求证A1P⊥BQ.
证明: 取DD1的中点R, 连接QR,AR, 如图:
AR∩A1P=O
∵Q是CC1的中点,∴QR平行且等于CD. 而AB平行且等于CD,
∴QR平行且等于AB, ∴四边形ABQRR是平行四边形,∴BQ//AR
在正方形AA1D1D中,∵P , R分别是AD, DD1的中点,
∴Rt△AA1P≌Rt△DAR, ∴∠AA1P=∠DAR.
∵∠DAR+∠A1AR=90°, ∴∠AA1P+∠A1AR =90°
∴∠AOA1=90°,
即A1P⊥AR, ∴A1P⊥BQ .
12. 如图,m, n是两条相交直线,l1, l2是与m, n都垂直的两条直
线,且直线l与l1,l2都相交,求证∠1=∠2.
解答
证明: ∵m, n是两条相交直线, l1, l2是与m, n都垂直
的两条直线,
∴两条直线分别垂直于m, n的平面,
∴l1和l2平行,
此时,若l与l1和l2相交,说明,三条直线在同一个
平面内, 且l与l1和l2相交,
∴∠1,∠2为同位角,根据两直线平行同位角相等,
可得: ∠1=∠2, 得证.
证明: 设两平行线为a, b, 平面为α.
①a, b都平行于α或都在α内,或一条与α平行,另一条在α内时,
a, b和α所成 的角都等于0°, ∴ a,b与α成等角;②a,b都和α垂直时,a, b和α所成的角都等于90°;
③a,b和α斜交时,如图, 设a∩α=A,b∩α= B, 在a,b.上分别取点C,D,
使C,D在α的同侧,作CE⊥α于E,DF⊥α于F, 则CE∥DF ,连结AE,BF,则直线AE,BF分别是a,b在α内的射影,∴∠CAE,∠DBF
分别是a, b和α所成的角。 ∵a∥b, CE∥DF,且∠ACE和∠BDF的方向相同,
∴∠ACE=∠BDF , ∴∠CAE=∠DBF,即斜线a, b与α所成的角相等.
综上所述,两条平行线和同一平面所成的角相等.
13. 求证:两条平行直线与同一个平面所成的角相等.
14.如下页圏,在棱锥V-ABC中, VO⊥平面ABC, O∈CD, VA=VB,
AD= BD, 你能判定CD⊥AB, 以及AC= BC吗
解答
VA= VB, AD= BD→VD⊥AB, VO⊥平面ABC,
AB 平面ABC上
→VO⊥AB
→AB⊥平面VCD, CD 平面VCD→AB⊥CD
即CD⊥AB
又AD= BD, CD= CD, ∠BDC= ∠ADC= 90°
△ADC≌△BD→AC= BC
15. 如图. 在正方形SG1G2G3中, E. F分别是G1G2, G2G3
的中点. D是EF的中点,若沿SE, SF及EF把这个正方形
折成一个四面体, 使G1, G2, G3三点重合, 重合后的点
记为G. 则在四面体S-EFC中,哪些棱与面互相垂直
解答
∵在折叠过程中,
始终有SG1⊥G1E,SG3⊥G3F,
即SG⊥GE,SG⊥GF ,
所以SG⊥平面EFG.
16.求证: 垂直于两个平行平面中的一个平面的直线也垂直于另一
个平面.
已知: α∥β,a⊥α,求证: α⊥β.
证明: 如图,过直线a作两平面γ,δ, 使
γ∩α=b,γ∩β=b',δ∩α=c,δ∩β=c',
∵α∥β,根据面面平行的性质, ∴b∥b' ,c//c'
∵a⊥α, b α, c α,∴a⊥b, a⊥c.
∴a⊥b', a⊥c'.
又b'与c'都在β内且相交,∴α⊥β.
17.求证: 三个两两亚直的平面的交线也两两垂直.
解答
设三个互相垂直的平面分别为α、β、γ, 且α∩β= a,
β∩γ=b,
γna=c, 三个平面的公共点为O, 如图所示:
在平面γ内,除点O外, 任意取一点M , 过点M作MN⊥c,MP⊥b,
M、P为垂足, 则有平面和平面垂直的性质可得MN⊥α , MP⊥β,
∴a⊥MN,a⊥MP,∴a⊥平面γ.
再由b、c在平面γ内, 可得a⊥b,a⊥c.
同理可证,c⊥b, c⊥a, 从而证得a、b、c互相垂直.
18.如图. 在三棱锥V-ABC中, VA=VB=VB=AC=BC=2, VC=1. 作出二面角V-AB-C的平面角.并求出它的余弦值.
解:如答图所示, 取AB的中点M, 连接VM, CM.
∵VA=VB,AC=BC
∴VM⊥AB, CM⊥AB
∴∠VMC为二面角V-AB-C的平面角
19. 如图.在直三棱柱ABC-A1B1C1中, ∠ABC=90°,AA1
=AB. 求证A1C⊥AB1.
证明: 连接A1B. ∵ABC-A1B1C1为直三棱柱
∴BB1⊥平面ABC,BC 平面ABC ∴BB1⊥BC
又∵∠ABC= 90°,∴AB⊥BC
∵BC⊥BB1,BC⊥AB, BB1 平面ABB1A1, AB 平面ABB1A1,
BB1∩AB=B
∴BC⊥平面ABB1A1, AB1 平面ABB1A1 ∴BC⊥AB1
∵AA1=AB,在正方形ABB1A1中,对角线AB1⊥A1B
∵AB1⊥A1B,AB1⊥BC,A1B 平面A1BC,BC 平面A1BC
A1B∩BC =B
∴AB⊥平面A1BC, A1 平面A1BC,∴A1C⊥AB1.
20. 如图,AB是⊙O的直径,点C是⊙O上的动点,过动点C的直
线VC垂直于⊙O所在平面,D,E分别是VA,VC的中点. 判断
直线DE平面VC的位置关系. 并说明理由.
证明:∵AC⊥BC, VC⊥AC,
∴AC⊥面VBC,
∵D、E分別カVC、VA中点,
∴DE∥AC,
∴DE⊥面VBC.
21.如图. 在四棱锥P-ABC中. 底面ABCD为正方形.
PA⊥底面ABCD. PA=AB, E为线段PB的中点. F为线
段BC上的动点,平面AEF与平面PBC是否互相垂直
如果垂直,请证明: 如果不垂直,请说明理由.
平面AEF与平面PBC互相垂直 理由如下:
因为PA⊥底面ABCD,BC 平面ABCD, 所以PA⊥BC.
因为ABCD为正方形,所以AB⊥BC
又PA∩AB=A,且PA, AB 平面PAB,
所以BC⊥平面PAB.
因为AE 平面PAB,所以AE⊥BC.
因为PA= AB,E为线段PB的中点,所以AE⊥PB,
又PB∩BC=B,且PB,BC 平面PBC,所以AE⊥平面PBC,
因为AE 平面AEF,所以平面AEF⊥平面PBC.
1.求二面角大小的步骤
作
作出平面角
证
证明所作的角满足定义,即为所求二面角的
平面角
求
将作出的 角放在三角形中,计算出平面角的
大小
简称为“一作二证三求”.
总结
总结
2.平面与平面垂直的判定定理的应用思路
(1) 本质: 通过直线与平面垂直来证明平面与平面垂直,即线面垂
直→面面垂直.
(2) 证题思路: 处理面面垂直问题转化为处理线面垂直问题,进一
步转化为处理线线垂直问题来解决.
空间直线、平面的垂直
教学目标
异面直线所成角、直线与平面所成角、二面角的定义;
直线与直线、直线与平面、平面与平面垂直的判定定理,异面
直线所成角、直线和平面所成的角、二面角及其求法;
异面直线垂直、直线与平面垂直、平面与平面垂直的判定定理
的综合应用.
教学重点
教学难点
异面直线所成的角、直线与平面所成的角、二面角的求解;
异面直线垂直、直线与平面垂直、平面与平面垂直的判定.
找异面直线所成的角、直线与平面所成的角、二面角;
异面直线垂直、直线与平面垂直、平面与平面垂直的判定定
理的应用.
引入
空间中两条直线的位置关系
1.空间两条直线的位置关系有三种:__________、_________、_________.
异面直线
平行直线
相交直线
2.分类
(1)从有无公共点的角度来看,可分为两类
平行直线
无公共点
(2)从是否共面的角度来看,可分为两类
相交直线
共面直线
直线
平行直线
不共面直线:异面直线
有且仅有一个公共点:相交直线
直线
异面直线
直线与直线垂直
异面直线a与b所成的角
1.如图,己知两条异面直线a, b经过空间任一点O分别作直线a'∥a,
b'∥b, 我们把直线a'与b'所成的角叫做_________________________
(或夹角).
0°≤a≤90°
2.范围:______________.
3.当θ=____时,a与b互相垂直,记作______.
异面直线所成角的范围是0°<θ≤90°,所以垂直有两种情况:
异面垂直和相交垂直.
4.当两条直线a,b相互平行时,我们规定它们所成的角为________.
所以空间两条直线所成角α的取值范围是________________.
0°<θ≤90°
a⊥b
90°
0°
[教材解难]
求异面直线所成的角的步骤
(1)找出(或作出)适合题设的角——用平移法, 遇题设中有中点,
常考虑中位线;若异面直线依附于某几何体,且对异面直线平移
有困难时,可利用该几何体的特殊点,使异面直线转化为相交
直线.
(2)求——转化为一个三角形的内角,通过解三角形,求出所找的
角.
(3)结论——设由(2)所求得的角的大小为θ. 若0°<θ≤90°,则θ为
所求;若90°<θ≤180°,则180°- θ为所求.
例1如图8.6-3, 已知正方体ABCD-A'B'C'D'.
(1)哪些棱所在的直线与直线 AA'垂直?
(2)求直线BA'与CC'所成的角的大小.
(3)求直线BA'与AC所成的角的大小.
解: (1)棱AB, BC, CD, DA, A'B', B'C', C'D', D'A'所在直线分别与直线AA'垂直.
(2)因为ABCD-A'B'C'D'是正方体,所以BB'∥CC, 因此∠A'BB'为直线BA'与
CC'所成的角. 又因为∠A'BB'=45°, 所以直线BA'与CC所成的角等于45°.
(3)如图8.6-4,连接A'C', 因为ABCD-A'B'C'D'是正方体,所以AA'⊥CC'.从
而四边形AA'C'C是平行四边形,所以AC//A'C.于是∠BA'C'为异面直线
BA'与AC所成的角,
连接BC',易知△A'BC'是等边三角形,所以∠BA'C'=60°.从而异面直线BA'
与AC所成的角等于60°.
例 在正方体 ABCD-A1B1C1D1中,E, F分别是A1B1, B1C1的中点,
求异面直线DB1与EF所成的角的大小.
拓展练习
[解] 方法一 如图所示, 连接A1C1, B1D1, 并设它们相交于点O,
取DD1的中点G, 连接OG, A1G, C1G,
则OG// B1D,EF//A1C1,
∴∠GOA1为异面直线DB1与EF所成的角(或其补角)
∵GA1=GC1, O为A1C1的中点,∴GO⊥A1C1.
∴异面直线DB1与EF所成的角为90°.
方法二 如图所示,连接A1D, 取A1D的中点H, 连接HE,则HE∥
∴∠HEF为异面直线DB1与EF所成的角(或其补角).
方法三:如图,连接A1C1, 分别取AA1, CC1的中点M, N,连接MN.
∵E, F分别是A1B1, B1C1的中点,
∴EF//A1C1, 又MN// A1C1, ∴MN// EF.
连接DM, B1N, MB1, DN, 则B1N//DM,
∴四边形DMB1N为平行四边形,∴MN与DB1必相交,
设交点为P,则∠DPM 为异面直线DB1与EF所成的角(或其补角).
方法四: 如图,在原正方体的右侧补上一个与其大小相等的正方体,
连接B1Q,易得B1Q// EF,
∴∠DB1Q就是异面直线DB1与EF所成的角(或其补角).
方法归纳
求异面直线所成角的步骤
一作: 选择适当的点,用平移法作出异面直线所成的角;
二证: 证明作出的角就是要求的角;
三计算: 将异面直线所成的角放入某个三角形中,利用特殊三角形
求解.
例2如图,在正方体ABCD-A1B1C1D1中,O1为底面A1B1C1D1的中心,
求证AO1⊥BD.
[证明] 如图,连接B1D1
∵ABCD-A1B1C1D1是正方体, ∴BB1∥DD1.
∴四边形BB1D1D是平行四边形, ∴B1D1// BD.
∴直线AO1与B1D1所成的角即为直线AO1与BD所成
的角. 连接AB1, AD1, 易证AB1=AD1.
又O1为底面A1B1C1D1的中心, ∴O1为B1D1的中点
∴AO1⊥B1D1, ∴AO1⊥BD.
方法归纳
证明直线与直线垂直的方法
①等腰三角形中线即是高线.
②勾股定理.
③异面直线所成的角为直角.
证明: 如图,取AC的中点F, 连接DF, EF,
在△PAC中,∵D是PC的中点,F是AC的中点,
∴DF//PA, 同理可得EF// BC,
∴∠DFE为异面直线PA与BC所成的角(或其补角).
在△DEF中,DE=3,
1.判所下列命题是否正确, 正确的在括号内画"√".错误的画“×".
(1)如果两条平行直线中的一条与已知直线垂直,那么另一条也
与已知直线垂直. ( )
(2)垂直于同一条直线的两条直线平行 ( )
2.如图, 在长方体ABCD-A'B'C'D'的各条棱所在直线中.
(1)与直线AB垂直的直线有____条;
(2)与直线AB异面且垂直的直线有____条;
(3)与直线AB和A'D'都垂直的直线有____条;
(4)与直线AB和A'D'都垂直且相交的直线是______.
8
4
4
1
(1)直线BC和AC'所成的角的大小:
(2)直线AA'和BC"所成的角的大小.
(1)因为BC∥BC ,所以∠B'C'A'是异面直线A'C'与BC所成的角
4.如图. 在正三棱柱ABC-A'B'C'中. D为棱AC的中点. AB=BB'=2.
求证BD⊥AC'.
引入
定义
画法
直线与平面垂直
如果直线l与平面α内的__________直线都______,就说
直线l与平面α互相垂直,记作.直线_____. 直线l叫作平
面α的_____,平面α叫作直线l的_____,直线与平面垂
直时,它们唯一的公共点P叫作______.
任意一条
垂直
l⊥a
垂线
垂面
垂足
通常把直线画成与表示平面的平行四边形的一边垂直,
如图
PO为垂线段,其长度为点P到面α的距离
垂线段
过一点垂直于已知平面的直线有且只有一条
文字语言: 如果一条直线与一个平面内的_____________________,
则该直线与此平面垂直.
直线与平面垂直的判定定理
两条相交直线垂直
图形语言:如图所示.
1.直线与平面垂直是直线与平面相交的特殊情形.
2.注意定义中“任意一条直线”与“所有直线”等同但不可说成“无数
条直线”.
3.判定定理条件中的“两条相交直线”是关键性词语,此处强调“相
交”,若两条直线平行,则直线与平面不一定垂直.
证明: 如图8.6-13,在平面α内取两条相交直线m, n,
∴直线a⊥α, ∴a⊥m, a⊥n.
∵b//a, ∴b⊥m, b⊥n.
又m α, n α, m,n是两条相交直线,
∴b⊥α.
例3 求证:如果两条平行直线中的一条直线垂直于一个平面,那
么另一条直线也垂直于这个平面.
已知: 如图8.6-12, a//b, a⊥α, 求证b⊥α.
例 如图所示, 已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC, AC=BC, N是AB的中点.求证: CN⊥平面ABB1A1.
AA1⊥底面ABC
CN 底面ABC
AA1⊥CN
AC=BC
N是AB的中点
AB⊥CN ,
又AA1 平面ABB1A1, AB 平面ABB1A1, AA1∩AB=A,所以
CN⊥平面ABB1A1.
证明
方法归纳
线面垂直的判定定理实质是由线线垂直推证线面垂直,途径是找到
一条直线与平面内的两条相交直线垂直. 推证线线垂直时注意分析
几何图形,寻找隐含条件.
直线与平面所成的角
直线和平面所成的角
当直线与平面垂直时,它们所成的角是90°.当直线与平面
平行或在平面内时,它们所成的角是___.
定义
范围
画法
平面的一条斜线和它在平面上的_____所成的___,叫作这
条直线和这个平面所成的角.
射影
角
0°
如图,______就是斜线AP与平面α所成的角
0°≤θ≤90°
∠PAO
把握定义应注意两点: ①斜线上不同于斜足的点P 的选取是任意的;
②斜线在平面上的射影是过斜足和垂足的一条直线而不是线段.
例4 如图,在正方体ABCD-A1B1C1D1中, 求直线A1B和平面
A1DCB1所成的角.
解 连接BC1, BC1与B1C相交于点O, 连接A1O.
设正方体的棱长为a.
∵A1B1⊥B1C1, A1B1⊥B1B, B1C1∩B1B=B1,
∴A1B1⊥平面BCC1B1. ∴A1B1⊥BC1.
又BC1⊥B1C, ∴BC1⊥平面A1DCB1.
方法归纳
求直线与平面所成的角的步骤
(1)作: 在斜线上选取恰当的点向平面引垂线,在这一步确定垂足的
位置是关键;
(2)证: 证明所找到的角为直线与平面所成的角,证明的主要依据为
直线与平面所成的角的定义;
(3)求: 一般来说是借助三角形的相关知识求角.
1.如果两条直线和一个平面所成的角相等,那么这两条直线一定
平行吗
两条直线与一个平面所成的角相等,则这两条直线相交、平行
或异面,例如圆锥的两条母线,与底面所成角相等,但是母线
是相交直线.
2.如图. 四梭锥S-ABCD的底面是正方形. SD⊥平面ABCD. 求证:
AC⊥平面SDB.
解答 ∵四棱柱A1B1C1D1-ABCD是直棱柱,
∴B1D1⊥A1A, 若A1C⊥B1D1
则B1D1⊥平面A1AC1C
∴B1D1⊥AC,
又由B1D∥BD,
则有BD⊥AC,
反之,由BD⊥AC亦可得到A1C⊥B1D1
故答案为: BD⊥AC.
3.如图,在直四棱柱A'B'C'D'-ABCD中,当底面四边形ABCD满
足什么条件时,A'C⊥B'D'? .
4. 过△ABC所在平面α外一点P. 作PO⊥α, 垂足为O. 连接PA, PB,
PC.
(1)若PA=PB=PC, 则点O是△ABC的___心.
(2)若PA=PB=PC, ∠C=90°, 则点O是AB边的___点
(3)若PA⊥PB, PB⊥PC, PC⊥PA, 垂足都为P.则点O是△ABC的___
心.
外
中
垂
直线与平面垂直的性质
①线面垂直→线线平行;
②作平行线
文字语言
垂直于同一个平面的两条直线_____
平行
符号语言
图形语言
作用
a//b
a⊥α
b⊥α
→_____
1.直线与平面垂直的性质定理给出了判定两条直线平行的另一种方
法.
2.定理揭示了空间中“平行”与“垂直”关系的内在联系,提供了
“垂直”与“平行”关系转化的依据.
例5 如图8.6-19, 直线l平行于平面α, 求证: 直线l上各点到平面
α的距离相等.
证明:过直线l上任意两点A, B分别作平面α的垂线AA1, BB1,
垂足分别为A1, B.
∵AA1⊥α, BB⊥α.
∴AA1//AB1
设直线AA1, BB1确定的平面为β. β∩α= A1B1
∵l//α
∴l//A1B1
∴四边形AA1B1B是矩形,
∴AA1= BB1.
由A, B是直线l上任取的两点. 可知直线l上各点到平面α的距离相等.
一条直线与一个平面平行时,这条直线上任意一点到这个平面的距
离,叫做这条直线到这个平面的距离. 由例5我们还可以进一步得出,
如果两个平面平行,那么其中一个平面内的任意一点到另一个平面
的距离都相等. 我们把它叫做这两个平行平面间的距离.
例6 推导棱台的体积公式
其中S',S分别是棱台的上、下底面面积,h是高.
解: 如图8.6-20. 延长棱台各侧棱交于点P. 得到截得棱台的
棱锥. 过点P作棱台的下底面的垂线,分别与梭台的上、下
底面交于点O', 则PO垂直于棱台的上底面(想一想,为什么
?). 从而O'O=h.
设藏得棱台的棱锥的体积为V, 去掉的棱锥的体积为V'、高为h', 则PO'=h'.
于是
由棱台的上、下底面平行. 可以证明棱台的上、下底面相似, 所以
例在正方体ABCD-A1B1C1D1中,点E, F分别在A1D, AC上,
EF⊥A1D, EF⊥AC, 求证: EF//BD1.
[证明]如图所示, 连接A1C1, C1D, B1D1, BD.
∵AC//A1C1, EF⊥AC, ∴EF⊥A1C1.
又EF⊥A1D, A1D∩AC1=A1, ∴EF⊥平面A1C1D1 ①
∵BB1⊥平面A1B1C1D1, A1C1 平面A1B1C1D1,
∴BB1⊥A1C1
∵四边形A1B1C1D1为正方形, ∴A1C1⊥B1D1,
又B1D1∩BB1=B1, ∴A1C1⊥平面BB1D1D,
而BD1 平面BB1D1D, ∴A1C1⊥BD1. 同理DC1⊥BD1.
又DC1∩A1C1=C1, ∴BD1⊥平面A1C1D. ②
由①②可知EF// BD1.
方法归纳
线面垂直的性质定理是证明两直线平行的重要依据,证明两直线平
行的常用方法:
(1)a//b, b//c→a//c.
(2)a//α, a β, β∩α=b→a// b.
(3)α//β, γ∩α=a, γ∩β=b→a//b.
(4)a⊥α, b⊥α→a//b.
1.已知直线a, b和平面α, 且a⊥b, a⊥α, 则b与a的位置关系是
_______.
a//b
2.已知A, B两点在平面α的同侧,且它们与α的距离相等,求证:
直线AB//α.
证明: 作出点A、B到α的垂线段AA'、BB'.
AA'平行且等于BB'→AA'BB'是平行四边形
→AB//A'B', AB α,A'B' α→AB//α.
3.如图,EA和DC都垂直于平面ABC, 且EA=2DC, F是EB的中点,
求证: DF //平面ABC.
∴FG∥CD,FG=CD,
∵FG⊥平面ABC,
∴四边形CDFG是矩形,DF∥CG,
CG 平面ABC,DF不包含于平面ABC,
∴DF∥平面ABC.
4.求证: 垂直于同一条直线的两个平面互相平行. (提示:过这条直
线作平面与这两个平面相交,则它们的交线平行.)
证明:设直线为l,平面为α,β.
而l⊥α,l⊥β. 则过l作平面m,
且l 平面m, 则
假设m∩α=l1, m∩β=l2.
由提示 l1∥l2,
又l1 α, l2 α,则l2∥α.
同理过l作平面n,使n∩α=l3, n∩β=l4.
则同理l4∥平面α.
又l3 β,l4 β,则α∥β.
二面角
图示
平面内的一条直线把平面分成两部分,这两部分通常称
为_______. 从这一条直线出发的____________所组成的图
形叫做二面角. 这条直线叫做二面角的___, 这两个半平
面叫做二面角的___.
概念
半平面
两个半平面
棱
面
平
面
角
OA α,OB β, α∩β=l, O∈l, OA⊥l, OB⊥l→∠AOB
是二面角的平面角.
文字
图示
符号
范围
规定
在二面角的棱上任取一点,以该点为垂足,在两个半平面内
分别作垂直于___的射线,则这两条射线构成的___叫做这个
二面角的平面角
棱
角
二面角的大小可以用它的________来度量, 二面角的平面角是多
___________________
0°≤∠AOB≤180°
少度,就说这个二面角是多少度, 平面角是_____ 的二面角叫做
直二面角
直角
平面角
棱为l,面分别为α, β的二面角记为_________ . 如图所示,
也可在α, β内(棱以外的半平面部分)分别取点P, Q, 将这个
二面角记作二面角__________.
记法
a-1- β
P-l-Q
无关如图,根据等角定理可知,∠AOB=∠A'O'B', 即二面角的平面
角的大小与角的顶点的位置无关,只与二面角的大小有关.
1.二面角与平面几何中的角有什么区别
平面几何中的角是从一点出发的两条射线组成的图形; 二面角是从
一条直线出发的两个半平面所组成的图形.
2.二面角的平面角的大小,与角的顶点在棱上的位置有关吗
例 下列命题中:
①两个相交平面组成的图形叫做二面角; ②异面直线a, b分别和一
个二面角的两个面垂直,则a, b所成的角与这个二面角的平面角
相等或互补; ③二面角的平面角是从棱上一点出发,分别在两个
面内作射线所成的角的最小角; ④二面角的大小与其平面角的
顶点在棱上的位置没有关系.其中正确的是 ( ) A.①③ B.②④ C.③④ D.①②
拓展练习
解析 由二面角的定义: 从一条直线出发的两个半平面所组成的图形
叫做二面角, 所以①不对,实质上它共有四个二面角; 由a,b分别垂
直于两个面,则a, b都垂直于二面角的棱,故②正确; ③中所作的
射线不一定垂直于二面角的棱,故③不对; 由定义知④正确. 故选B.
答案B
规律方法
1.要注意区别二面角与两相交平面所成的角并不一致.
2.要注意二面角的平面角与顶点在棱上且角两边分别在二面角面
内的角的联系与区别.
3.可利用实物模型,作图帮助判断.
1. 定义: 两个平面相交,如果它们所成的二面角是___________, 就
说这两个平面互相垂直. 平面α与平面β垂直,记作________.
2.画法: 两个互相垂直的平面通常把直立平面的竖边画成与水平平
面的______垂直.如图所示.
平面与平面垂直
直二面角
α⊥β
横边
平面与平面垂直的判定定理
l⊥α, ______ →α⊥β
文字语言
图形语言
符号语言
一个平面过另一个平面的_______,则这两个平面
垂直
垂线
l β
例7如图 8.6-27所示,在正方体ABCD-A'B'C'D'中,求证: 平面
A'BD⊥平面ACC'A'.
证明: ∵ABCD-A'B'C'D'是正方体,
∴AA⊥平面ABCD.
∴AA'⊥ BD.
又BD⊥AC.
∴BD⊥平面ACC'A'.
∴平而A'BD⊥平面ACC'A'.
例8如图8.6-28. AB是⊙O的直径, PA垂直于⊙O所在的平面,
C是圆周上不同于A,B的任意一点. 求证: 平面PAC⊥平面PBC.
证明: ∵PA⊥平面ABC,
BC 平面ABC.
∴PA⊥BC.
∵点C是圆周上不同于A, B的任意一点, AB是⊙O的直
径,
∴∠BCA=90°, 即BC⊥AC.
又PA∩AC=A, PA 平面PAC, AC 平面PAC,
∴BC⊥平面PAC,
又BC 平面PBC,
∴平面PAC⊥平面PBC.
拓展练习
如图所示,AB是⊙O的直径,PA垂直于⊙O所在的平
面,C是圆周上的一点,且PA=AC, 求二面角P-BC-A
的大小
解 ∵PA⊥平面ABC, BC 平面ABС,
∴PA⊥ВС.
∵AB是⊙O的直径,且点C在圆周上,∴AC⊥BC.
又∵РА∩AC=А, ∴BC⊥平面PAC.
而PC 平面PAC, ∴PC⊥BC.
又∵BC是二面角P-BC-A的棱,
∴∠PCA是二面角P-BC-A的平面角.
由PA=AC知,△PAC是等腰直角三角形,
∴∠PCA=45°,即二面角P-BC-A的大小是45°.
规律方法 确定二面角的平面角的方法:
(1)定义法: 在二面角的棱上找一特殊点,在两个半平面内分别作垂
直于棱的射线.
(2)垂面法: 过棱上一点作棱的垂直平面,该平面与二面角的两个半
平面产生交线,这两条交线所成的角,即为二面角的平面角.
(3)线面垂直法: 该法就是利用线面垂直来寻找二面角的平面角,是
最常用的也是最好用的一种方法. 由一个半平面内异于棱上的点A向
另一半平面作垂线,垂足为点B, 由B点向二面角的棱作垂线,垂足
为点O, 连接AO, 则∠AOB为二面角的平面角(或其补角) .
空间中的垂直关系
1.如图。检查工作的相邻两个(平)面是否垂直时,只要用曲尺的
一边紧靠在工件的一个面上,另一边在工件的另一个面上转动,
观察尺边和这个面是否密合就可以了, 这是为什么
解答
检查工件的相邻的两个面是否垂直时,只要
用曲尺的一边紧靠在工件的一个面上,
另一边在工件的另一个面上转动一下,若曲尺的另一
边和工件的另一面密合, 就说明工件的另一个面经过
工件的一个面的垂线, 由面面垂直的判定定理得工件
的这两个互相垂直。 如果不转运,无法判断曲尺的
另一边和工件的另一面是否密合, 也就无法判断工件
的相邻的两个面是否垂直.
2.已知直线a, b与平面α, β, γ. 能使α⊥β的充分条件是( ).
(A)α⊥γ ,β⊥γ
(B)α∩β=a, b⊥a, b β
(C) a// , a//α
(D) a//α, a⊥β
D
3.如下页图. AB⊥平面BCD,BC⊥CD. 你能发现哪些平面互相
垂直,为什么?
解答 平面ABC⊥平面BCD, 平面ABD⊥平面BCD, 平面ACD⊥平
面ABC
4.如图,在正三棱柱ABC-A'B'C'中,D为棱AC的中点.求证: 平
面BDC'⊥平面ACC'A'.
证明: ∵ A'A⊥平面ABC
BD 平面ABC
∴A'A⊥BD
∵△ABC是正三角形, D为棱AC的中点
∴BD⊥AC
∵BD⊥A'A ,BD⊥AC,AA' 平面ACC'A,AC 平面ACC'A,
A'A∩AC=A→BD⊥平面ACC'A
又∵BD 平面BDC'
∴BDC'⊥平面ACC'A'
平面与平面垂直的性质定理
两个平面垂直,则一个平面内垂直于交线的直线与另
一个平面______
垂直
文字语言
符号语言
a⊥β
a∩β=l
a α
a⊥l
→a⊥β
图形语言
作用
证明直线与平面垂直
例9如图8. 6-32.已知平面α⊥平面β. 直线a⊥β, a α. 判断a与α的
位置关系.
解:在α内作垂直于α与β交线的直线b,
∵α⊥β.
∴b⊥β.
又a⊥β.
∴a//b.
又a α.
∴a//α.
即直线a与平面α平行.
例 如图8.6-33, 已知PA⊥平面ABC,平面PAB⊥平面PBC.
求证: BC⊥平面PAB.
证明:如图8.6-34,过点A作AE⊥PB, 垂足为E.
∵平面PAB⊥平面PBC,平面PAB∩平面PBC=PB,
∴AE⊥平面PBC,
∵BC 平面PBC,
∴AE⊥BC.
∵PA⊥平面ABC, BC 平面ABC,
∴PA⊥BC.
又PA∩AE=А,
∴BC⊥平面PAB.
拓展练习
如图所示, P是四边形ABCD所在平面外的一点,四边形ABCD是
∠DAB=60°的菱形,侧面PAD为正三角形, 其所在平面垂直于底面
ABCD. 若G为AD边的中点,求证:BG⊥平面PAD.
拓展练习
证明: 连接PG, BD,
∵四边形ABCD是菱形且∠DAB= 60°,
∴△ABD是正三角形,
∵G是AD的中点,
∴BG⊥AD.
又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴BG⊥平面PAD.
规律总结
1. 若所给题目中有面面垂直的条件,一般要利用面面垂直的定理
将其转化为线面垂直、线线垂直. 在应用面面垂直的性质定理时,注意三点: ①两个平面垂直,是前提条件; ②直线必须在其中一个
平面内; ③直线必须垂直于它们的交线.
2. 先找条件中有没有在一个平面内与交线垂直的直线,若没有与
交线垂直的直线,一般需作辅助线, 基本作法是过其中一个平面内
一点作交线的垂线, 这样便把面面垂直问题转化为线面垂直问题,
进而转化为线线垂直问题.
1. 判断下列命题是否正确,正确的在括号内画“√”,错误的画
“×”.
(1)如果平面α⊥平面β, 那么平面α内所有直线都垂直于平面β.
( )
(2)如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β.
( )
(3)如果平面α不垂直于平面β,那么平面a内一定不存在直线垂直
于平面β.
( )
2. 若平面α⊥平面β,且a∩β=l, 则下列命题中正确的个数是( )
(1)平面α内的直线必垂直于平面β内的任意一条直线.
(2)平面α内的已知直线必垂直于平面β内的无数条直线.
(3)平面α内的任一条直线必垂直于平面β.
(4)过平面α内任意一点作交线l的垂线,则此垂线必垂直于平面β.
(A) 3 (B) 2 (C) 1 (D) 0
B
3.已知α,β是两个不同的平面,m为平面α内的一条直线,则
“α⊥β”是“m⊥β”的( ).
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
B
解答
设过直线 a与平面α内的一点的平面与α的交线为a'.
∵a∥α, ∴a∥a'.
∵a⊥AB,
∴a'⊥AB.
∵a' α,α⊥β,
∴a'⊥β.
∴a⊥β, 即a与β的位置关系是a⊥β.
4. 已知平面α,β. 直线a, 且α⊥β,α∩β=AB. a//α, a⊥AB. 判断直
线a与平面β的位置关系. 并说明理由.
1.选择题
(1)若空间中四条不同的直线l1, l2, l3, l4满足l1⊥l2, l2⊥l3, l3⊥l4. 则下面
结论正确的是( ).
(A)l1⊥l4 (B)l1//l4
(C) l1, l4既不垂直也不平行 (D)l1, l4的位置关系不确定
(2) 设l, m, n均为直线. 其中m, n在平面α内. 则"l⊥α”是"l⊥m"且“l⊥n”
的( ).
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
(3)直线l1, l2互相平行的一个充分条件是( )
(A)l1, l2都平行于同一个平面 (B) l1, l2与同一个平面所成的角相等
(C) l1, l2都垂直于同一个平面 (D)l1平行于l2所在的平面
D
A
D
2.判断下列命题是个正确,正确的在括号内画"√",错误的画"X".
(1)过平面外一点,有且只有一条直线与这个平面垂直. ( )
(2)过平面外一点,有且只有一条直线与这个平面平行. ( )
(3)过直线外一点,有且只有一个平面与这条直线垂直. ( )
(4)过直线外一点,有且只有一个平面与这条直线平行. ( )
(5)过直线外一点,有且只有一条直线与这条直线平行. ( )
3.判断下列命题是否正确. 正确的说明理由, 错误的举例说明.
(1) 一条直线行于一个平面,另一条直线与这个平面垂直,则这两条
直线互相垂直;
(2)如果平面α//平面α1,平面β//平面β1,那么平面α与平面β所成的
二面角和平面α1与与平面β1所成的二面角相等或互补;
(3)如果平面α⊥平面β,平面β⊥平面γ,那么平而α⊥平面γ.
解: (1)正确, 设直线a//平面α , 直线b⊥平面α , 则存在直线c α,且a//c, ∴b⊥c, ∴b⊥a.
(2)正确, 两个平面平行, 则其法向量也平行, 两个二面角的两个半平
面的法向量所成角相等或互补;
(3)错误, 如长方体中两底面都与同一侧面垂直, 但两底面不垂直.
4. 如图, 在直二棱柱ABC-A1B1C1中, CA=CB, P为AB
的中点, Q为棱C1C的中点. 求证:
(1)PQ⊥AB; (2) PQ⊥C1C; (3) PQ⊥A1B.
证明: (1)如图, 取AB的中点D ,连接CD、DP,
∴PD//CQ , ∴四边形CDPQ为平行四边形, ∴CD//PQ.
又∵CACB , D为AB的中点,∴CD⊥AB,∴PQ⊥AB .
(2)在直三棱柱ABC-A1B1C1中, AA1⊥平面ABC, CD 平面ABC,
∴AA1⊥CD , 由(1)知CD//PQ, ∴PQ⊥AA1. 又AA1//CC1,∴PQ⊥CC1.
(3)由(1) (2)知, PQ⊥AB,PQ⊥AA1, 而AB∩AA1=A.
∴PQ⊥平面AA1B1B. ∵A1B 平面AA1B1B, ∴PQ⊥A1B .
5. 如图,在三棱锥P-ABC中,CD⊥AB,垂足为D,
PO⊥底面ABC, 垂足为O,且O在CD上, 求证AB⊥PC.
证明: ∵PO⊥底面ABC, AB 底面ABC, ∴PO⊥AB.
∵O在CD上,∴PO∩CD=O.
又CD⊥AB
∴AB⊥平面POC,∵PC 平面POC, ∴AB⊥PC.
6.如图,在正方体ABCD-A'B'C'D'中,平面ABC'D'与正方
体的各个面所在的平面所成的二面角的大小分别是多少?
解: 在正方体ABCD-A'B'C'D'中,考虑平面ABC'D'与平面ABCD ,
AB⊥平面B'C'CB , BC', BC 平面B'C'CB , 所以平面∠B'BC就是平面ABC'D'与
平面ABCD所成角, 即平面ABC'D'与平面ABCD成角∠C'BC=45°.
同理平面ABC'D'与平面ABCD, 平面A'B'C'D' , 平面ABB'A' , 平面CC'D'D都成
45°角,
又因为AB⊥平面ADD'A' , 平面ABC'D'与平面ADD'A'垂直, 即所成的角为90° ,
同理可得平面ABC'D'与平面ADD'A' , 平面BCC'B'都垂直, 即与它们所成的角为
90°.
所以平面ABC'D'与平面ABCD, 平面A'B'C'D' , 平面ABB'A' , 平面CC'D'D都成
45°角, 平面ABC'D'与平面ADD'A', 平面BCC'B'都垂直, 即与它们所成的角为90°.
7.如图,在三棱锥V-ABC中,已知∠VAB=∠VAC=
∠ABC=90°,判断平面VAB与平面VBC的位置关系,
并说明理由.
解答
∵∠VAB=∠VAC=90°, ∴ VA⊥AB, VA⊥AC, 又AB∩AC= A,
∴VA⊥平面ABC,∴VA⊥BC.
∠ABC=90° , ∴AB⊥BC , VA∩VB= V,
∴BC⊥平面VBA,又ВC 平面VBC,
∴平面VBA⊥平面VBC.
8. 求证:如果共点的三条直线两两垂直,那么它们中每两条直线确
定的平面也两两垂直.
解答
已知: 直线a,b,c共点且两两垂直,直线a和b确定的平面为α, 直
线a和c确定的平面为β, 直线b和c确定的平面为γ,
求证: a⊥γ,b⊥β,c⊥α,
证明: ∵直线a, b,c共点且两两垂直, 直线b和c确定的平面为γ,
∴由直线与平面垂直的判定定理可得a⊥γ,同理可证b⊥β,c⊥α,
∴原命题得证
解答
证明: 如图,
∵平面α⊥平面γ,
∴平面α与平面γ相交, 设交线为m ,
在平面α内作直线a⊥m, ∵平面α⊥平面γ,∴a⊥γ,
在平面β内任取一点O, 由直线a和点O确定平面M,设M∩β于b,
∵平面α∥平面β, 由面面平行的判定定理, 得a∥b,
∵a// b,a⊥γ, ∴b⊥γ
又∵b β,
∴平面β⊥平面γ.
9. 已知平面α, β, γ,且α⊥γ, β//α, 求证β⊥γ.
10. 已知平面α, β, γ, 且α⊥γ, β⊥γ, α∩β=l, 求证l⊥γ.
解答
证明: 如图, 在平面内γ任取一点P,
过点P作PA⊥l1, PB⊥l2,A,B为垂足.
∵α∩γ=l1,α⊥γ, PA γ, ∴PA⊥α
又∵l α, ∴PA⊥I.
同理: PB⊥l,
∴l⊥γ.
11. 如图,在正方体ABCD-A1B1C1D1中,点P, Q分别为棱AD, CC1
的中点, 求证A1P⊥BQ.
证明: 取DD1的中点R, 连接QR,AR, 如图:
AR∩A1P=O
∵Q是CC1的中点,∴QR平行且等于CD. 而AB平行且等于CD,
∴QR平行且等于AB, ∴四边形ABQRR是平行四边形,∴BQ//AR
在正方形AA1D1D中,∵P , R分别是AD, DD1的中点,
∴Rt△AA1P≌Rt△DAR, ∴∠AA1P=∠DAR.
∵∠DAR+∠A1AR=90°, ∴∠AA1P+∠A1AR =90°
∴∠AOA1=90°,
即A1P⊥AR, ∴A1P⊥BQ .
12. 如图,m, n是两条相交直线,l1, l2是与m, n都垂直的两条直
线,且直线l与l1,l2都相交,求证∠1=∠2.
解答
证明: ∵m, n是两条相交直线, l1, l2是与m, n都垂直
的两条直线,
∴两条直线分别垂直于m, n的平面,
∴l1和l2平行,
此时,若l与l1和l2相交,说明,三条直线在同一个
平面内, 且l与l1和l2相交,
∴∠1,∠2为同位角,根据两直线平行同位角相等,
可得: ∠1=∠2, 得证.
证明: 设两平行线为a, b, 平面为α.
①a, b都平行于α或都在α内,或一条与α平行,另一条在α内时,
a, b和α所成 的角都等于0°, ∴ a,b与α成等角;②a,b都和α垂直时,a, b和α所成的角都等于90°;
③a,b和α斜交时,如图, 设a∩α=A,b∩α= B, 在a,b.上分别取点C,D,
使C,D在α的同侧,作CE⊥α于E,DF⊥α于F, 则CE∥DF ,连结AE,BF,则直线AE,BF分别是a,b在α内的射影,∴∠CAE,∠DBF
分别是a, b和α所成的角。 ∵a∥b, CE∥DF,且∠ACE和∠BDF的方向相同,
∴∠ACE=∠BDF , ∴∠CAE=∠DBF,即斜线a, b与α所成的角相等.
综上所述,两条平行线和同一平面所成的角相等.
13. 求证:两条平行直线与同一个平面所成的角相等.
14.如下页圏,在棱锥V-ABC中, VO⊥平面ABC, O∈CD, VA=VB,
AD= BD, 你能判定CD⊥AB, 以及AC= BC吗
解答
VA= VB, AD= BD→VD⊥AB, VO⊥平面ABC,
AB 平面ABC上
→VO⊥AB
→AB⊥平面VCD, CD 平面VCD→AB⊥CD
即CD⊥AB
又AD= BD, CD= CD, ∠BDC= ∠ADC= 90°
△ADC≌△BD→AC= BC
15. 如图. 在正方形SG1G2G3中, E. F分别是G1G2, G2G3
的中点. D是EF的中点,若沿SE, SF及EF把这个正方形
折成一个四面体, 使G1, G2, G3三点重合, 重合后的点
记为G. 则在四面体S-EFC中,哪些棱与面互相垂直
解答
∵在折叠过程中,
始终有SG1⊥G1E,SG3⊥G3F,
即SG⊥GE,SG⊥GF ,
所以SG⊥平面EFG.
16.求证: 垂直于两个平行平面中的一个平面的直线也垂直于另一
个平面.
已知: α∥β,a⊥α,求证: α⊥β.
证明: 如图,过直线a作两平面γ,δ, 使
γ∩α=b,γ∩β=b',δ∩α=c,δ∩β=c',
∵α∥β,根据面面平行的性质, ∴b∥b' ,c//c'
∵a⊥α, b α, c α,∴a⊥b, a⊥c.
∴a⊥b', a⊥c'.
又b'与c'都在β内且相交,∴α⊥β.
17.求证: 三个两两亚直的平面的交线也两两垂直.
解答
设三个互相垂直的平面分别为α、β、γ, 且α∩β= a,
β∩γ=b,
γna=c, 三个平面的公共点为O, 如图所示:
在平面γ内,除点O外, 任意取一点M , 过点M作MN⊥c,MP⊥b,
M、P为垂足, 则有平面和平面垂直的性质可得MN⊥α , MP⊥β,
∴a⊥MN,a⊥MP,∴a⊥平面γ.
再由b、c在平面γ内, 可得a⊥b,a⊥c.
同理可证,c⊥b, c⊥a, 从而证得a、b、c互相垂直.
18.如图. 在三棱锥V-ABC中, VA=VB=VB=AC=BC=2, VC=1. 作出二面角V-AB-C的平面角.并求出它的余弦值.
解:如答图所示, 取AB的中点M, 连接VM, CM.
∵VA=VB,AC=BC
∴VM⊥AB, CM⊥AB
∴∠VMC为二面角V-AB-C的平面角
19. 如图.在直三棱柱ABC-A1B1C1中, ∠ABC=90°,AA1
=AB. 求证A1C⊥AB1.
证明: 连接A1B. ∵ABC-A1B1C1为直三棱柱
∴BB1⊥平面ABC,BC 平面ABC ∴BB1⊥BC
又∵∠ABC= 90°,∴AB⊥BC
∵BC⊥BB1,BC⊥AB, BB1 平面ABB1A1, AB 平面ABB1A1,
BB1∩AB=B
∴BC⊥平面ABB1A1, AB1 平面ABB1A1 ∴BC⊥AB1
∵AA1=AB,在正方形ABB1A1中,对角线AB1⊥A1B
∵AB1⊥A1B,AB1⊥BC,A1B 平面A1BC,BC 平面A1BC
A1B∩BC =B
∴AB⊥平面A1BC, A1 平面A1BC,∴A1C⊥AB1.
20. 如图,AB是⊙O的直径,点C是⊙O上的动点,过动点C的直
线VC垂直于⊙O所在平面,D,E分别是VA,VC的中点. 判断
直线DE平面VC的位置关系. 并说明理由.
证明:∵AC⊥BC, VC⊥AC,
∴AC⊥面VBC,
∵D、E分別カVC、VA中点,
∴DE∥AC,
∴DE⊥面VBC.
21.如图. 在四棱锥P-ABC中. 底面ABCD为正方形.
PA⊥底面ABCD. PA=AB, E为线段PB的中点. F为线
段BC上的动点,平面AEF与平面PBC是否互相垂直
如果垂直,请证明: 如果不垂直,请说明理由.
平面AEF与平面PBC互相垂直 理由如下:
因为PA⊥底面ABCD,BC 平面ABCD, 所以PA⊥BC.
因为ABCD为正方形,所以AB⊥BC
又PA∩AB=A,且PA, AB 平面PAB,
所以BC⊥平面PAB.
因为AE 平面PAB,所以AE⊥BC.
因为PA= AB,E为线段PB的中点,所以AE⊥PB,
又PB∩BC=B,且PB,BC 平面PBC,所以AE⊥平面PBC,
因为AE 平面AEF,所以平面AEF⊥平面PBC.
1.求二面角大小的步骤
作
作出平面角
证
证明所作的角满足定义,即为所求二面角的
平面角
求
将作出的 角放在三角形中,计算出平面角的
大小
简称为“一作二证三求”.
总结
总结
2.平面与平面垂直的判定定理的应用思路
(1) 本质: 通过直线与平面垂直来证明平面与平面垂直,即线面垂
直→面面垂直.
(2) 证题思路: 处理面面垂直问题转化为处理线面垂直问题,进一
步转化为处理线线垂直问题来解决.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
