10.3 频率与概率 课件(27张PPT)
文档属性
| 名称 | 10.3 频率与概率 课件(27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-22 00:05:54 | ||
图片预览








文档简介
(共27张PPT)
频率与概率
教学目标
通过试验,理解当试验次数较大时试验频率稳定于理论概率,并可据此估计 一事件发生的概率。
能运用树状图和列表法计算简单事件发生的概率。
教学重点
频率与概率的关系的理解。
教学重点
列表计算事件发生的频率,并与概率相比较。
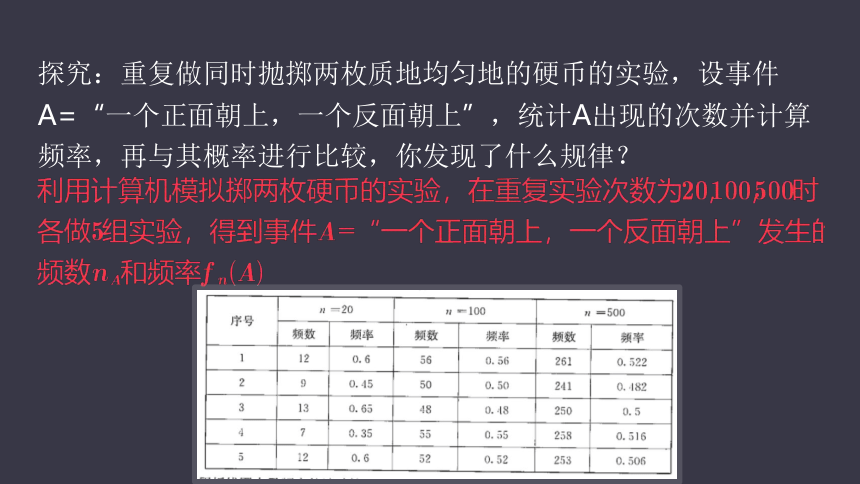
探究:重复做同时抛掷两枚质地均匀地的硬币的实验,设事件A=“一个正面朝上,一个反面朝上”,统计A出现的次数并计算频率,再与其概率进行比较,你发现了什么规律?
连续两次抛掷一枚硬币,一定是出现一次正面和一次反面吗?
概率具有随机性,试验次数太少的时候偏差容易很大。
探究:重复做同时抛掷两枚质地均匀地的硬币的实验,设事件A=“一个正面朝上,一个反面朝上”,统计A出现的次数并计算频率,再与其概率进行比较,你发现了什么规律?
探究:重复做同时抛掷两枚质地均匀地的硬币的实验,设事件A=“一个正面朝上,一个反面朝上”,统计A出现的次数并计算频率,再与其概率进行比较,你发现了什么规律?
频率与概率
频率和概率的区别与联系:
联系:概率是频率的稳定值;
区别:频率具有随机性,概率是一个确定的数;
范围:[0,1].
频率与概率
天气预报说昨天的降水概率为 90%,结果昨天根本没下雨,能否认为这次天气预报不准确?如何根据频率与概率的关系判断这个天气预报是否正确?
不能,概率为90%的事件发生的可能性很大,但“明天下雨”是随即事件,也有可能不发生.收集近50年同日的天气情况,考察这一天下雨的频率是否为90%左右.
1、新生婴儿性别比是每100名女婴对应的男婴数,通过抽样调查得知,我国2014年、2015年出生的婴儿性别分别为115.88和113.51.
(1) 分别估计我国2014年和2015年的男婴的出生率(新生儿中男婴的比率,精确到0.001);
(2) 根据估计结果,你认为“生男孩和生女孩是等可能的“ 这个判断可靠吗?
(2) 由于调查新生儿人数的样本非常大,根据频率的稳定性,上述对男婴出生率的估计值具有较高的可信度.因此,我们有理由怀疑“生男孩和生女孩是等可能的”的结论.
2、一个游戏包内含两个随机事件A和B,规定事件A发生则甲获胜,事件B发生则乙获胜,判断游戏是否公平的标准是事件A和B发生的概率是否相等.
在游戏过程中,甲发现:玩了10次时,双方各胜5次;但玩到1000次是,自己才胜300次,而乙却胜了700次,据此,甲认为游戏不公平,但乙认为游戏是公平的,你更支持谁的结论?为什么?
当游戏玩到1000次时,甲、乙获胜的频率分别为0.3和0.7,存在很大的差距,所以有理由认为游戏时不公平的.
1、判断下列说法是否正确,并说明理由:
(1) 抛掷一枚硬币正面朝上的概率为0.5,则抛掷两枚硬币,一定是一次正面朝上,一次是反面朝上;
(2) 抛掷一枚质地均匀的硬币10次,结果是4次正面朝上,所以事件“正面朝上”的概率为0.4;
(3) 当实验次数很大时,随机事件发生的频率接近其概率;
(4) 在一次实验中,随机事件可能发生也可能不发生,所以事件发生和不发生的概率各是0.5.
(1) 错,概率并不会严格发生,具有随机性;
(2) 错,样本过少;(3) 对
(4) 错,概率并不相同
2、用掷两枚硬币作胜负游戏,规定:两枚硬币同时出现正面或负面算甲胜,一个正面,一个负面算乙胜利,这个游戏公平吗?
公平
3、据统计ABO血型具有民族和地区差异,在我国H省调查了30188人,四种血型的人数如下:
(1)计算H省血型的频率并填表(精确到0.001)
(2)如果从H省任意调查一个人的血型,那么他是O型血的概率大约是多少
血型
人数/人
频率
A
B
O
D
7701
10765
8970
3049
0.253
0.353
0.294
0.100
4、分别举出一个生活中概率很小和很大的概率.
概率很小:买彩票中五百万;
概率很大:买彩票没中奖。
1、某射击运动员射击击中目标的概率为97%,估计该运动员射击1000次命中的次数为______.
970
C
16
4、有人批发黄豆3000kg,验得黄豆内混有少量豌豆,两种豆子大小均匀、质量相等.抽样取豆一把226颗,数得豆内混有豌豆3颗,则这批黄豆内混有豌豆约_________kg(结果精确到个位数)
40
1、用频率估计概率,需要做大量的重复实验.有没有其他方法可以替代实验呐?
我们知道,利用计算器或计算机软件可以产生随机数,实际上,我们也可以根据不同的随机实验构建相应的随机模拟实验,这样就可以快速地进行大量重复实验了.
我们称利用随机模拟解决问题的方法为蒙特卡洛.
1、从所在班级任意选出6名同学,调查它们的出生年月,假设出生在一月,二月......十二月是等可能的.舍事件A=“至少有两人出生年月份相同”,设计一种实验方法,模拟20次,估计事件A发生的概率.
0.70
2、有一次奥运会男子羽毛球比赛中,运动员甲和乙进入了决赛,假设每局比赛甲获胜的概率为0.6,乙获胜的概率是0.4,利用计算机模拟实验,估计甲获胜得冠军的概率.
甲获胜的概率为0.65
1、将一枚质地均匀的硬币连掷4次,设事件A="恰好两次正面朝上"
(1) 直接计算事件A的概率
(2) 利用计算器或计算机模拟实验80次,计算事件A发生的概率;
(1) P(A)=0.25
(2) 理论上应接近20次
2、盒子中仅有4个白球和5个黑球,从中任意取出一个球.
(1) "取出的球是黄球"是什么事件?它的概率是多少?
(2) "取出的球是白球"是什么事件?它的概率是多少?
(3) "取出的球是白球或黑球"是什么事件?它的概率是多少?
(4) 设计一个用计算器或计算机模拟上面取球的实验,并模拟100次,估计“取出的球是白球” 的概率.
(1) 不可能事件,概率为0
(4) 概率为0.45
3、(1) 掷两枚质地均匀的骰子,计算点数和为7的概率
(2) 利用随机模拟的方法,实验120次,计算出现点数和为7的概率
(3) 所得频率与概率相差大吗?为什么会有这种差异?
(2) 设计产生1、2、3、4、5和6这6个数的随机函数,出现400个,每相邻两个作为1组,和为7的记为“点数之和为7”这一事件发生,可得其频率;
(3) 一般来说频率与概率有一定的差距,因为模拟次数不多,不一定能反映真实情况。
掌握频率与概率的区别和联系
频率与概率
总结
频率与概率
频率的稳定性,用频率估计概率
了解计算机随机模拟大量重复实验的过程
频率与概率
教学目标
通过试验,理解当试验次数较大时试验频率稳定于理论概率,并可据此估计 一事件发生的概率。
能运用树状图和列表法计算简单事件发生的概率。
教学重点
频率与概率的关系的理解。
教学重点
列表计算事件发生的频率,并与概率相比较。
探究:重复做同时抛掷两枚质地均匀地的硬币的实验,设事件A=“一个正面朝上,一个反面朝上”,统计A出现的次数并计算频率,再与其概率进行比较,你发现了什么规律?
连续两次抛掷一枚硬币,一定是出现一次正面和一次反面吗?
概率具有随机性,试验次数太少的时候偏差容易很大。
探究:重复做同时抛掷两枚质地均匀地的硬币的实验,设事件A=“一个正面朝上,一个反面朝上”,统计A出现的次数并计算频率,再与其概率进行比较,你发现了什么规律?
探究:重复做同时抛掷两枚质地均匀地的硬币的实验,设事件A=“一个正面朝上,一个反面朝上”,统计A出现的次数并计算频率,再与其概率进行比较,你发现了什么规律?
频率与概率
频率和概率的区别与联系:
联系:概率是频率的稳定值;
区别:频率具有随机性,概率是一个确定的数;
范围:[0,1].
频率与概率
天气预报说昨天的降水概率为 90%,结果昨天根本没下雨,能否认为这次天气预报不准确?如何根据频率与概率的关系判断这个天气预报是否正确?
不能,概率为90%的事件发生的可能性很大,但“明天下雨”是随即事件,也有可能不发生.收集近50年同日的天气情况,考察这一天下雨的频率是否为90%左右.
1、新生婴儿性别比是每100名女婴对应的男婴数,通过抽样调查得知,我国2014年、2015年出生的婴儿性别分别为115.88和113.51.
(1) 分别估计我国2014年和2015年的男婴的出生率(新生儿中男婴的比率,精确到0.001);
(2) 根据估计结果,你认为“生男孩和生女孩是等可能的“ 这个判断可靠吗?
(2) 由于调查新生儿人数的样本非常大,根据频率的稳定性,上述对男婴出生率的估计值具有较高的可信度.因此,我们有理由怀疑“生男孩和生女孩是等可能的”的结论.
2、一个游戏包内含两个随机事件A和B,规定事件A发生则甲获胜,事件B发生则乙获胜,判断游戏是否公平的标准是事件A和B发生的概率是否相等.
在游戏过程中,甲发现:玩了10次时,双方各胜5次;但玩到1000次是,自己才胜300次,而乙却胜了700次,据此,甲认为游戏不公平,但乙认为游戏是公平的,你更支持谁的结论?为什么?
当游戏玩到1000次时,甲、乙获胜的频率分别为0.3和0.7,存在很大的差距,所以有理由认为游戏时不公平的.
1、判断下列说法是否正确,并说明理由:
(1) 抛掷一枚硬币正面朝上的概率为0.5,则抛掷两枚硬币,一定是一次正面朝上,一次是反面朝上;
(2) 抛掷一枚质地均匀的硬币10次,结果是4次正面朝上,所以事件“正面朝上”的概率为0.4;
(3) 当实验次数很大时,随机事件发生的频率接近其概率;
(4) 在一次实验中,随机事件可能发生也可能不发生,所以事件发生和不发生的概率各是0.5.
(1) 错,概率并不会严格发生,具有随机性;
(2) 错,样本过少;(3) 对
(4) 错,概率并不相同
2、用掷两枚硬币作胜负游戏,规定:两枚硬币同时出现正面或负面算甲胜,一个正面,一个负面算乙胜利,这个游戏公平吗?
公平
3、据统计ABO血型具有民族和地区差异,在我国H省调查了30188人,四种血型的人数如下:
(1)计算H省血型的频率并填表(精确到0.001)
(2)如果从H省任意调查一个人的血型,那么他是O型血的概率大约是多少
血型
人数/人
频率
A
B
O
D
7701
10765
8970
3049
0.253
0.353
0.294
0.100
4、分别举出一个生活中概率很小和很大的概率.
概率很小:买彩票中五百万;
概率很大:买彩票没中奖。
1、某射击运动员射击击中目标的概率为97%,估计该运动员射击1000次命中的次数为______.
970
C
16
4、有人批发黄豆3000kg,验得黄豆内混有少量豌豆,两种豆子大小均匀、质量相等.抽样取豆一把226颗,数得豆内混有豌豆3颗,则这批黄豆内混有豌豆约_________kg(结果精确到个位数)
40
1、用频率估计概率,需要做大量的重复实验.有没有其他方法可以替代实验呐?
我们知道,利用计算器或计算机软件可以产生随机数,实际上,我们也可以根据不同的随机实验构建相应的随机模拟实验,这样就可以快速地进行大量重复实验了.
我们称利用随机模拟解决问题的方法为蒙特卡洛.
1、从所在班级任意选出6名同学,调查它们的出生年月,假设出生在一月,二月......十二月是等可能的.舍事件A=“至少有两人出生年月份相同”,设计一种实验方法,模拟20次,估计事件A发生的概率.
0.70
2、有一次奥运会男子羽毛球比赛中,运动员甲和乙进入了决赛,假设每局比赛甲获胜的概率为0.6,乙获胜的概率是0.4,利用计算机模拟实验,估计甲获胜得冠军的概率.
甲获胜的概率为0.65
1、将一枚质地均匀的硬币连掷4次,设事件A="恰好两次正面朝上"
(1) 直接计算事件A的概率
(2) 利用计算器或计算机模拟实验80次,计算事件A发生的概率;
(1) P(A)=0.25
(2) 理论上应接近20次
2、盒子中仅有4个白球和5个黑球,从中任意取出一个球.
(1) "取出的球是黄球"是什么事件?它的概率是多少?
(2) "取出的球是白球"是什么事件?它的概率是多少?
(3) "取出的球是白球或黑球"是什么事件?它的概率是多少?
(4) 设计一个用计算器或计算机模拟上面取球的实验,并模拟100次,估计“取出的球是白球” 的概率.
(1) 不可能事件,概率为0
(4) 概率为0.45
3、(1) 掷两枚质地均匀的骰子,计算点数和为7的概率
(2) 利用随机模拟的方法,实验120次,计算出现点数和为7的概率
(3) 所得频率与概率相差大吗?为什么会有这种差异?
(2) 设计产生1、2、3、4、5和6这6个数的随机函数,出现400个,每相邻两个作为1组,和为7的记为“点数之和为7”这一事件发生,可得其频率;
(3) 一般来说频率与概率有一定的差距,因为模拟次数不多,不一定能反映真实情况。
掌握频率与概率的区别和联系
频率与概率
总结
频率与概率
频率的稳定性,用频率估计概率
了解计算机随机模拟大量重复实验的过程
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
