数学高中必修五苏教版1.2《余弦定理》课件2
文档属性
| 名称 | 数学高中必修五苏教版1.2《余弦定理》课件2 |  | |
| 格式 | zip | ||
| 文件大小 | 208.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-05 16:35:06 | ||
图片预览






文档简介
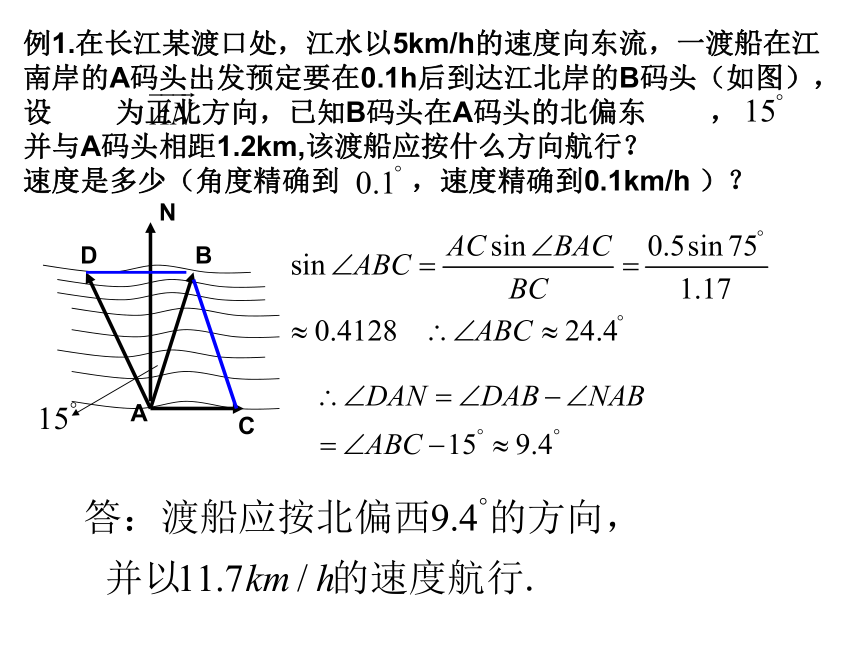
课件15张PPT。§1.2. 余弦定理 (2)知 识 改 变 命 运,勤 奋 成 就 未 来. 三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。余弦定理公式变形:课前复习例1.在长江某渡口处,江水以5km/h的速度向东流,一渡船在江南岸的A码头出发预定要在0.1h后到达江北岸的B码头(如图),设 为正北方向,已知B码头在A码头的北偏东 ,
并与A码头相距1.2km,该渡船应按什么方向航行?
速度是多少(角度精确到 ,速度精确到0.1km/h )?解:船按 方向开出, 方向为水流方向,以AC为一边,AB为对角线作平行四边形ABCD,其中,AB=1.2km,AC=5×0.1=0.5km例1.在长江某渡口处,江水以5km/h的速度向东流,一渡船在江南岸的A码头出发预定要在0.1h后到达江北岸的B码头(如图),设 为正北方向,已知B码头在A码头的北偏东 ,
并与A码头相距1.2km,该渡船应按什么方向航行?
速度是多少(角度精确到 ,速度精确到0.1km/h )?思考:想想看有无其它的方法?变式训练: 在△ABC中,若b2sin2C+c2sin2B
=2bc·cosBcosC,试判断三角形的形状。解:由正弦定理,
R为△ABC的外接圆半径,将原式化为4R2sin2Bsin2C+4R2sin2Csin2B
=8R2sinBsinCcosBcosC, 所以8R2sin2Bsin2C=8R2sinBsinCcosBcosC, 因为sinBsinC≠0,所以sinBsinC=cosBcosC,
即cos(B+C)=0, 从而∠B+∠C=90°,∠A=90°,
故△ABC为直角三角形。 解2:将已知等式变形为
b2(1-cos2C)+c2(1-cos2B)=2bccosBcosC,
由余弦定理得变式训练: 在△ABC中,若b2sin2C+c2sin2B
=2bc·cosBcosC,试判断三角形的形状。即得, 得b2+c2=a2,
故△ABC是直角三角形。 变式训练: 在△ABC中,若b2sin2C+c2sin2B
=2bc·cosBcosC,试判断三角形的形状。变式训练: 试用余弦定理证明平行四边形的两条对角线平方的和等于四边平方的和.例4. △ABC中,
(1)若
求∠A;
(2)若
求最大的内角。 解:(1)由正弦定理得a2=b2+c2+bc,
即b2+c2-a2=-bc,所以故∠A=120°; 解:(2)因为,
所以∠C为最大角,设a=( -1)k,b=( +1)k,c=10k,故最大内角C为120°.例4. △ABC中,
(1)若
求∠A;
(2)若
求最大的内角。 2. 在△ABC中,3. 在△ABC中,5. 在△ABC中,4. 在△ABC中,6. 在△ABC中,课堂小结运用余弦定理解决一些与测量和几何计算有关的实际问题2.根据条件判断三角形的形状3.证明恒等式4.与正弦定理结合解斜三角形
并与A码头相距1.2km,该渡船应按什么方向航行?
速度是多少(角度精确到 ,速度精确到0.1km/h )?解:船按 方向开出, 方向为水流方向,以AC为一边,AB为对角线作平行四边形ABCD,其中,AB=1.2km,AC=5×0.1=0.5km例1.在长江某渡口处,江水以5km/h的速度向东流,一渡船在江南岸的A码头出发预定要在0.1h后到达江北岸的B码头(如图),设 为正北方向,已知B码头在A码头的北偏东 ,
并与A码头相距1.2km,该渡船应按什么方向航行?
速度是多少(角度精确到 ,速度精确到0.1km/h )?思考:想想看有无其它的方法?变式训练: 在△ABC中,若b2sin2C+c2sin2B
=2bc·cosBcosC,试判断三角形的形状。解:由正弦定理,
R为△ABC的外接圆半径,将原式化为4R2sin2Bsin2C+4R2sin2Csin2B
=8R2sinBsinCcosBcosC, 所以8R2sin2Bsin2C=8R2sinBsinCcosBcosC, 因为sinBsinC≠0,所以sinBsinC=cosBcosC,
即cos(B+C)=0, 从而∠B+∠C=90°,∠A=90°,
故△ABC为直角三角形。 解2:将已知等式变形为
b2(1-cos2C)+c2(1-cos2B)=2bccosBcosC,
由余弦定理得变式训练: 在△ABC中,若b2sin2C+c2sin2B
=2bc·cosBcosC,试判断三角形的形状。即得, 得b2+c2=a2,
故△ABC是直角三角形。 变式训练: 在△ABC中,若b2sin2C+c2sin2B
=2bc·cosBcosC,试判断三角形的形状。变式训练: 试用余弦定理证明平行四边形的两条对角线平方的和等于四边平方的和.例4. △ABC中,
(1)若
求∠A;
(2)若
求最大的内角。 解:(1)由正弦定理得a2=b2+c2+bc,
即b2+c2-a2=-bc,所以故∠A=120°; 解:(2)因为,
所以∠C为最大角,设a=( -1)k,b=( +1)k,c=10k,故最大内角C为120°.例4. △ABC中,
(1)若
求∠A;
(2)若
求最大的内角。 2. 在△ABC中,3. 在△ABC中,5. 在△ABC中,4. 在△ABC中,6. 在△ABC中,课堂小结运用余弦定理解决一些与测量和几何计算有关的实际问题2.根据条件判断三角形的形状3.证明恒等式4.与正弦定理结合解斜三角形
