数学高中必修五苏教版1.1《正弦定理》课件2
文档属性
| 名称 | 数学高中必修五苏教版1.1《正弦定理》课件2 |

|
|
| 格式 | zip | ||
| 文件大小 | 155.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-05 16:36:34 | ||
图片预览




文档简介
课件19张PPT。正弦定理
(1)直角三角形中:
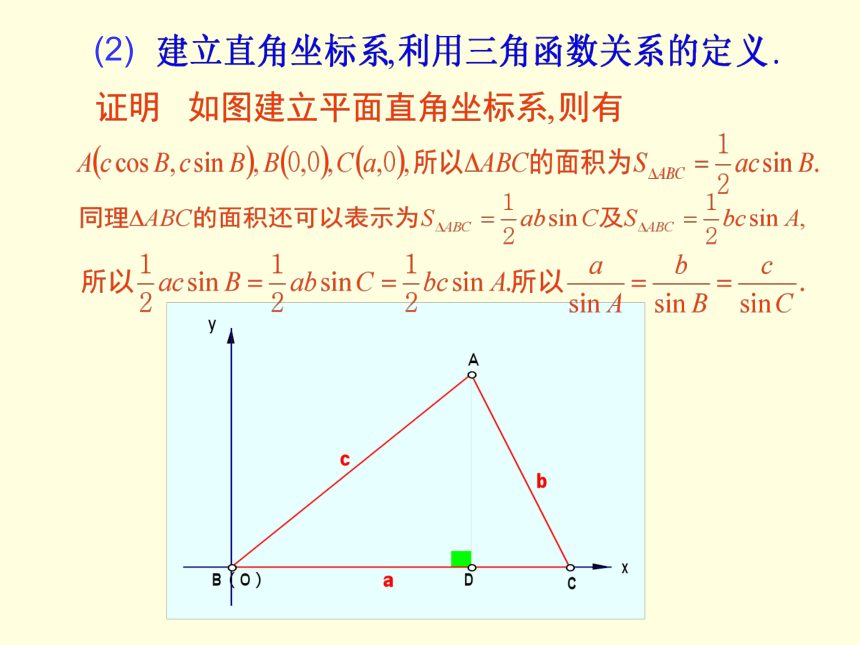
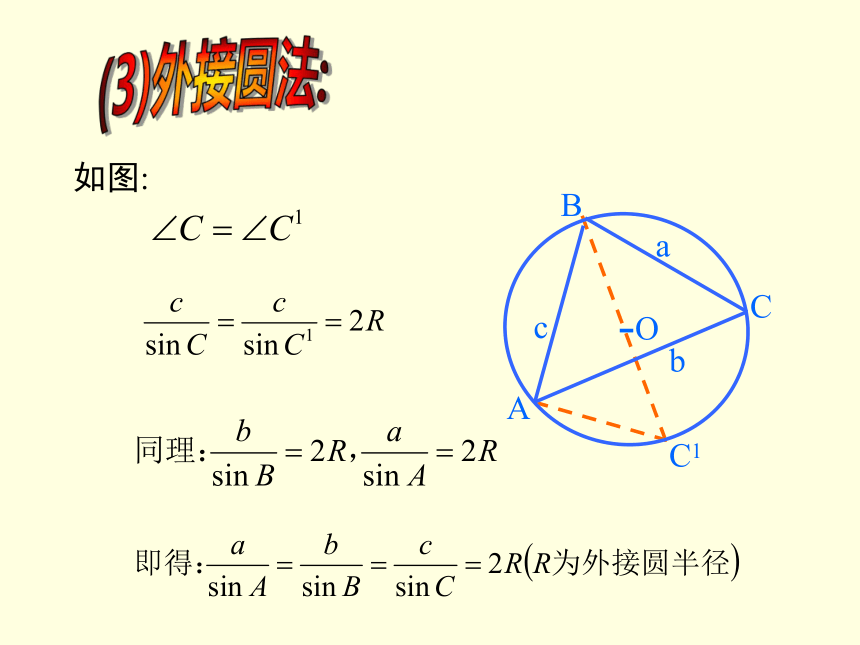
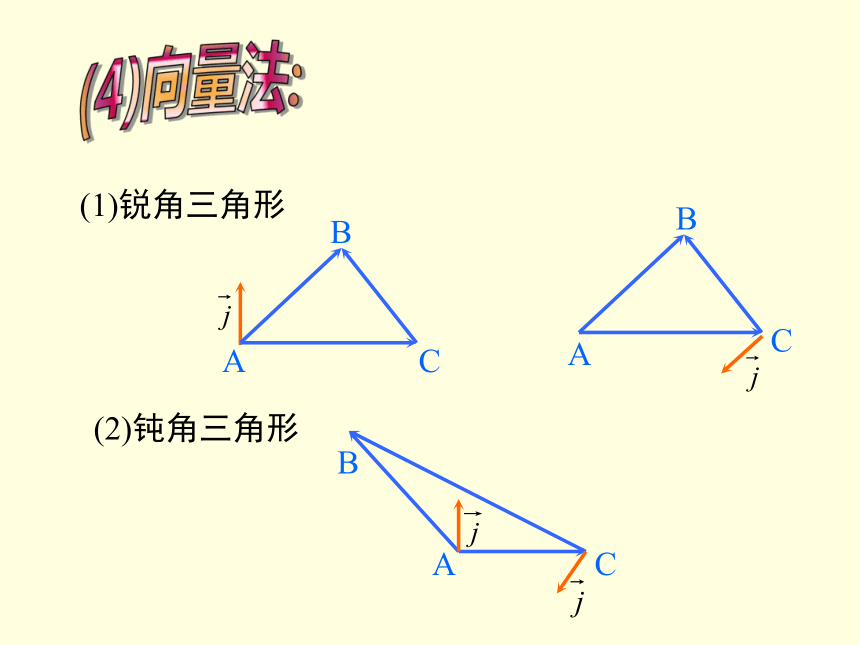
斜三角形中这一关系式是否仍成立呢?课题引入(2)如图:(3)外接圆法:(1)锐角三角形(2)钝角三角形(4)向量法:在一个三角形中,各边和它所对角的正弦的比相等,
即正弦定理变式:从理论上,正弦定理可解决两类问题:
两角和任意一边,求其他两边和一角
两边和其中一边对角,求另一边的对角,进而可求其他的边和角
正弦定理的应用(1)a=10,A=30o,C=45o; (2)A=30o,B=120o,b=12; (3) ①b=13,a=26,B=30o;
②b= ,c= ,B=45o;
③ b=2,c= ,B=45o.寻找发现规律例题 根据下列条件解三角形: 若A为锐角时:
若A为直角或钝角时:
已知a,b和A,用正弦定理求B时的各种情况: 用正弦定理,可以解决以下两类解斜三角形的问题:课堂小结 (1)已知三角形的两角与任一边,求其他两边和一角; (2)已知三角形的两边与其中一边的对角,求另一边的对角(从而进一步求出其他的边和角). 若已知三角形的两边和其中一边的对角,解三角形时可能会出现无解、唯一解、两解的情况,应注意判别解的情况.
例如已知a,b及A时 (1)若A≥90o 当a>b时,有一解;
当a≤b时,由“三角形中大边对大角”可知此时无解.课堂小结三角形解的个数问题:(2)若A<90o,又可有下表:课堂小结判断满足下列的三角形的个数:
(1)b=11, a=20, B=30o
(2)c=54, b=39, C=120o
(3)b=26, c=15, C=30o
(4)a=2,b=6,A=30o两解一解两解无解练习: 通过本节学习,我们一起研究了正弦定理的证明方法,同时了解了向量的工具性作用,并且明确了利用正弦定理所能解决的两类有关三角形问题:已知两角一边;已知两边和其中一边的对角.小结: 例1:已知在 中, ,
求 和
例2:已知在 中, ,
求 和点评:正弦定理可以用于解决已知两角和一边求另两边和一角的问题.点评:正弦定理也可用于解决已知两边及一边的对角,求其他边和角的问题.例题评析
(1)直角三角形中:
斜三角形中这一关系式是否仍成立呢?课题引入(2)如图:(3)外接圆法:(1)锐角三角形(2)钝角三角形(4)向量法:在一个三角形中,各边和它所对角的正弦的比相等,
即正弦定理变式:从理论上,正弦定理可解决两类问题:
两角和任意一边,求其他两边和一角
两边和其中一边对角,求另一边的对角,进而可求其他的边和角
正弦定理的应用(1)a=10,A=30o,C=45o; (2)A=30o,B=120o,b=12; (3) ①b=13,a=26,B=30o;
②b= ,c= ,B=45o;
③ b=2,c= ,B=45o.寻找发现规律例题 根据下列条件解三角形: 若A为锐角时:
若A为直角或钝角时:
已知a,b和A,用正弦定理求B时的各种情况: 用正弦定理,可以解决以下两类解斜三角形的问题:课堂小结 (1)已知三角形的两角与任一边,求其他两边和一角; (2)已知三角形的两边与其中一边的对角,求另一边的对角(从而进一步求出其他的边和角). 若已知三角形的两边和其中一边的对角,解三角形时可能会出现无解、唯一解、两解的情况,应注意判别解的情况.
例如已知a,b及A时 (1)若A≥90o 当a>b时,有一解;
当a≤b时,由“三角形中大边对大角”可知此时无解.课堂小结三角形解的个数问题:(2)若A<90o,又可有下表:课堂小结判断满足下列的三角形的个数:
(1)b=11, a=20, B=30o
(2)c=54, b=39, C=120o
(3)b=26, c=15, C=30o
(4)a=2,b=6,A=30o两解一解两解无解练习: 通过本节学习,我们一起研究了正弦定理的证明方法,同时了解了向量的工具性作用,并且明确了利用正弦定理所能解决的两类有关三角形问题:已知两角一边;已知两边和其中一边的对角.小结: 例1:已知在 中, ,
求 和
例2:已知在 中, ,
求 和点评:正弦定理可以用于解决已知两角和一边求另两边和一角的问题.点评:正弦定理也可用于解决已知两边及一边的对角,求其他边和角的问题.例题评析
