沪科版数学八年级下册 19.1多边形内角和 练习试题(word版含答案)
文档属性
| 名称 | 沪科版数学八年级下册 19.1多边形内角和 练习试题(word版含答案) | 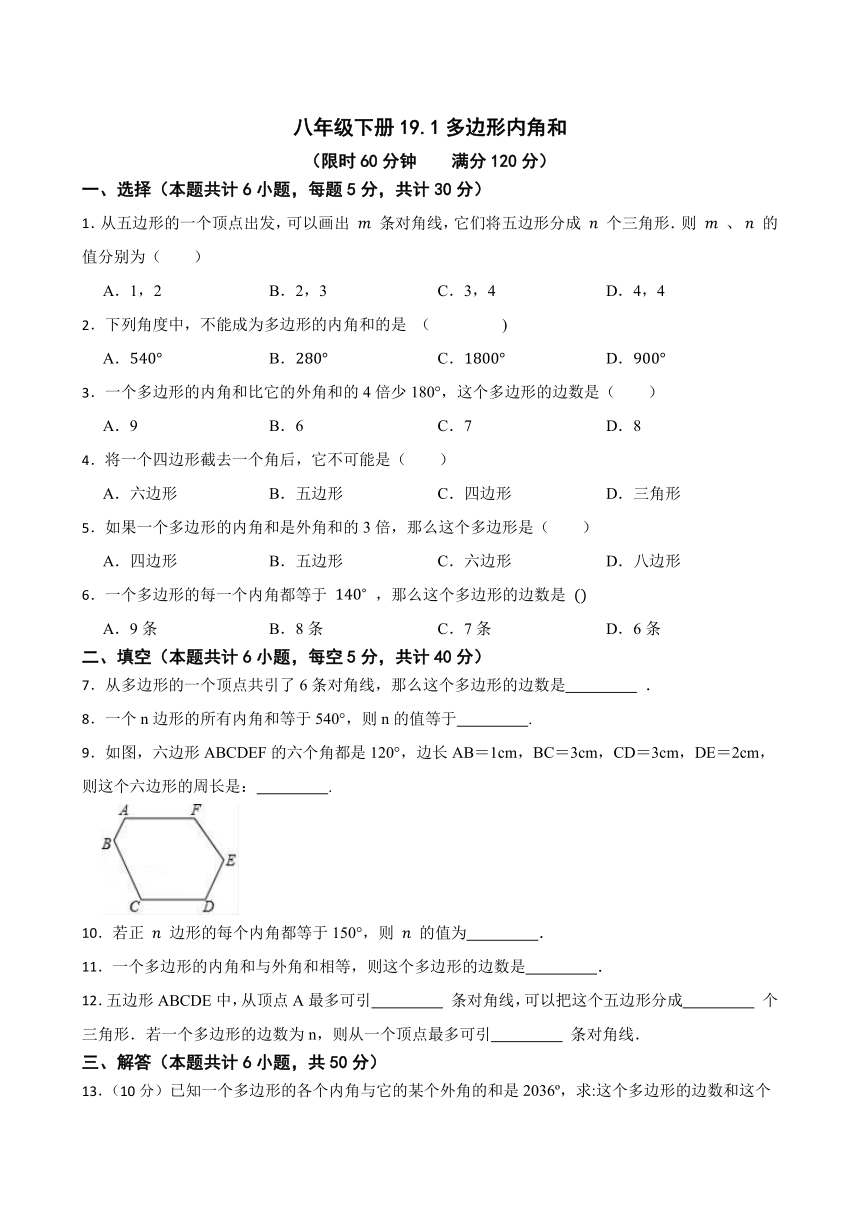 | |
| 格式 | docx | ||
| 文件大小 | 39.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-23 08:13:53 | ||
图片预览


文档简介
八年级下册19.1多边形内角和
(限时60分钟 满分120分)
一、选择(本题共计6小题,每题5分,共计30分)
1.从五边形的一个顶点出发,可以画出 条对角线,它们将五边形分成 个三角形.则 、 的值分别为( )
A.1,2 B.2,3 C.3,4 D.4,4
2.下列角度中,不能成为多边形的内角和的是 ( )
A. B. C. D.
3.一个多边形的内角和比它的外角和的4倍少180°,这个多边形的边数是( )
A.9 B.6 C.7 D.8
4.将一个四边形截去一个角后,它不可能是( )
A.六边形 B.五边形 C.四边形 D.三角形
5.如果一个多边形的内角和是外角和的3倍,那么这个多边形是( )
A.四边形 B.五边形 C.六边形 D.八边形
6.一个多边形的每一个内角都等于 ,那么这个多边形的边数是
A.9条 B.8条 C.7条 D.6条
二、填空(本题共计6小题,每空5分,共计40分)
7.从多边形的一个顶点共引了6条对角线,那么这个多边形的边数是 .
8.一个n边形的所有内角和等于540°,则n的值等于 .
9.如图,六边形ABCDEF的六个角都是120°,边长AB=1cm,BC=3cm,CD=3cm,DE=2cm,则这个六边形的周长是: .
10.若正 边形的每个内角都等于150°,则 的值为 .
11.一个多边形的内角和与外角和相等,则这个多边形的边数是 .
12.五边形ABCDE中,从顶点A最多可引 条对角线,可以把这个五边形分成 个三角形.若一个多边形的边数为n,则从一个顶点最多可引 条对角线.
三、解答(本题共计6小题,共50分)
13.(10分)已知一个多边形的各个内角与它的某个外角的和是2036 ,求:这个多边形的边数和这个外角的度数.
14.(10分)过m边形的一个顶点有8条对角线,n边形没有对角线,p边形有p条对角线,试求(m﹣p)n的值.
15.(10分)求下图中∠α的度数.
16.(10分)如图所示,在四边形ABCD中,∠A=80°,∠C=75°,∠ADE为四边形ABCD的一个外角,且∠ADE=125°,试求出∠B的度数.
17.(10分)如图所示,一块较为精密的模板中,AB,CD的延长线应该相交成80°的角,因交点不在模板上,不便测量,测得∠BAE=124°,∠DCF=155°,AE⊥EF,CF⊥EF,此时AB,CD的延长线相交成的角是否符合规定?为什么?
答案部分
1.B
2.B
3.A
4.A
5.D
6.A
7.9
8.5
9.15cm
10.12
11.4
12.2;3;n﹣3
13.解:2036÷180=11‥‥‥56,则n﹣2=11,解得:n=13.
答:它的边数是13,外角度数为56°
14.解:∵过m边形的一个顶点有8条对角线,
∴m﹣3=8,m=11;
n边形没有对角线,n=3;
∵p边形有p条对角线,
∴p=p(p﹣3)÷2,解得p=5,
所以(m﹣p)n=(11﹣5)3=216.
15.解:根据图中的数据可知:第一个图:α=360°-65°-70°-(180°-40°)=85°;
第二个图:α=180°-(360°-90°-90°-40°)=40°.
16.解:∵∠ADE为四边形ABCD的一个外角,且∠ADE=125°
∴∠ADC=180°-∠ADE=180°-125°=55°
∵∠A+∠B+∠C+∠ADC=360°
∴∠B=360°-∠A-∠C-∠ADC=360°-80°-75°-55°=150°.
17.解:设AB与CD的延长线相交于点G,如图,
则∠A+∠E+∠F+∠C+∠G=540°
∵AE⊥EF,CF⊥EF,
∴∠E=∠F=90°.
∵∠BAE=124°,∠DCF=155°
G=540°-(124°+155°+90°×2)=540°-459°=81°.
∴81°≠80°,
∴不符合规定。
(限时60分钟 满分120分)
一、选择(本题共计6小题,每题5分,共计30分)
1.从五边形的一个顶点出发,可以画出 条对角线,它们将五边形分成 个三角形.则 、 的值分别为( )
A.1,2 B.2,3 C.3,4 D.4,4
2.下列角度中,不能成为多边形的内角和的是 ( )
A. B. C. D.
3.一个多边形的内角和比它的外角和的4倍少180°,这个多边形的边数是( )
A.9 B.6 C.7 D.8
4.将一个四边形截去一个角后,它不可能是( )
A.六边形 B.五边形 C.四边形 D.三角形
5.如果一个多边形的内角和是外角和的3倍,那么这个多边形是( )
A.四边形 B.五边形 C.六边形 D.八边形
6.一个多边形的每一个内角都等于 ,那么这个多边形的边数是
A.9条 B.8条 C.7条 D.6条
二、填空(本题共计6小题,每空5分,共计40分)
7.从多边形的一个顶点共引了6条对角线,那么这个多边形的边数是 .
8.一个n边形的所有内角和等于540°,则n的值等于 .
9.如图,六边形ABCDEF的六个角都是120°,边长AB=1cm,BC=3cm,CD=3cm,DE=2cm,则这个六边形的周长是: .
10.若正 边形的每个内角都等于150°,则 的值为 .
11.一个多边形的内角和与外角和相等,则这个多边形的边数是 .
12.五边形ABCDE中,从顶点A最多可引 条对角线,可以把这个五边形分成 个三角形.若一个多边形的边数为n,则从一个顶点最多可引 条对角线.
三、解答(本题共计6小题,共50分)
13.(10分)已知一个多边形的各个内角与它的某个外角的和是2036 ,求:这个多边形的边数和这个外角的度数.
14.(10分)过m边形的一个顶点有8条对角线,n边形没有对角线,p边形有p条对角线,试求(m﹣p)n的值.
15.(10分)求下图中∠α的度数.
16.(10分)如图所示,在四边形ABCD中,∠A=80°,∠C=75°,∠ADE为四边形ABCD的一个外角,且∠ADE=125°,试求出∠B的度数.
17.(10分)如图所示,一块较为精密的模板中,AB,CD的延长线应该相交成80°的角,因交点不在模板上,不便测量,测得∠BAE=124°,∠DCF=155°,AE⊥EF,CF⊥EF,此时AB,CD的延长线相交成的角是否符合规定?为什么?
答案部分
1.B
2.B
3.A
4.A
5.D
6.A
7.9
8.5
9.15cm
10.12
11.4
12.2;3;n﹣3
13.解:2036÷180=11‥‥‥56,则n﹣2=11,解得:n=13.
答:它的边数是13,外角度数为56°
14.解:∵过m边形的一个顶点有8条对角线,
∴m﹣3=8,m=11;
n边形没有对角线,n=3;
∵p边形有p条对角线,
∴p=p(p﹣3)÷2,解得p=5,
所以(m﹣p)n=(11﹣5)3=216.
15.解:根据图中的数据可知:第一个图:α=360°-65°-70°-(180°-40°)=85°;
第二个图:α=180°-(360°-90°-90°-40°)=40°.
16.解:∵∠ADE为四边形ABCD的一个外角,且∠ADE=125°
∴∠ADC=180°-∠ADE=180°-125°=55°
∵∠A+∠B+∠C+∠ADC=360°
∴∠B=360°-∠A-∠C-∠ADC=360°-80°-75°-55°=150°.
17.解:设AB与CD的延长线相交于点G,如图,
则∠A+∠E+∠F+∠C+∠G=540°
∵AE⊥EF,CF⊥EF,
∴∠E=∠F=90°.
∵∠BAE=124°,∠DCF=155°
G=540°-(124°+155°+90°×2)=540°-459°=81°.
∴81°≠80°,
∴不符合规定。
