数学高中必修二苏教版1.3《空间几何体的表面积和体积》课件1
文档属性
| 名称 | 数学高中必修二苏教版1.3《空间几何体的表面积和体积》课件1 |  | |
| 格式 | zip | ||
| 文件大小 | 77.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-05 22:26:38 | ||
图片预览



文档简介
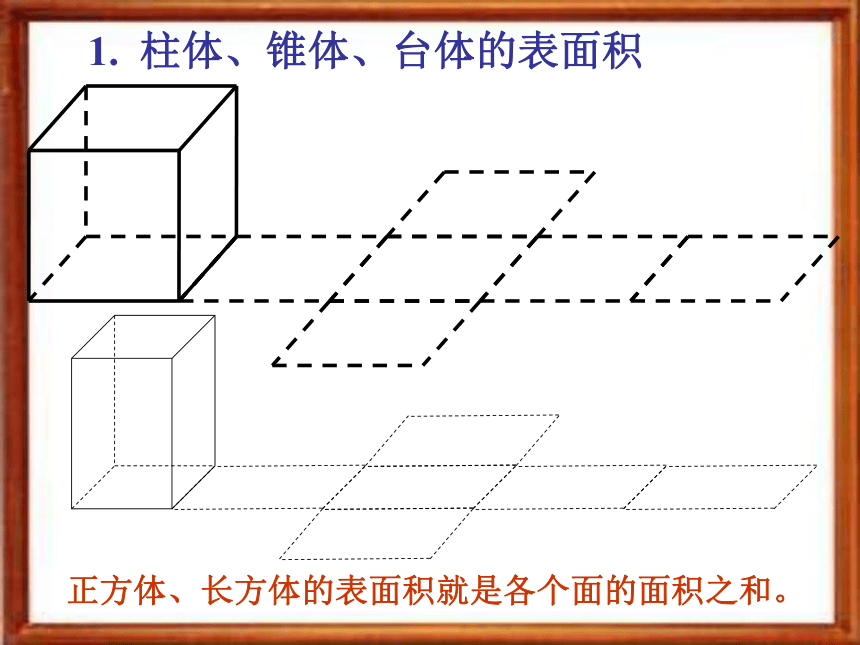
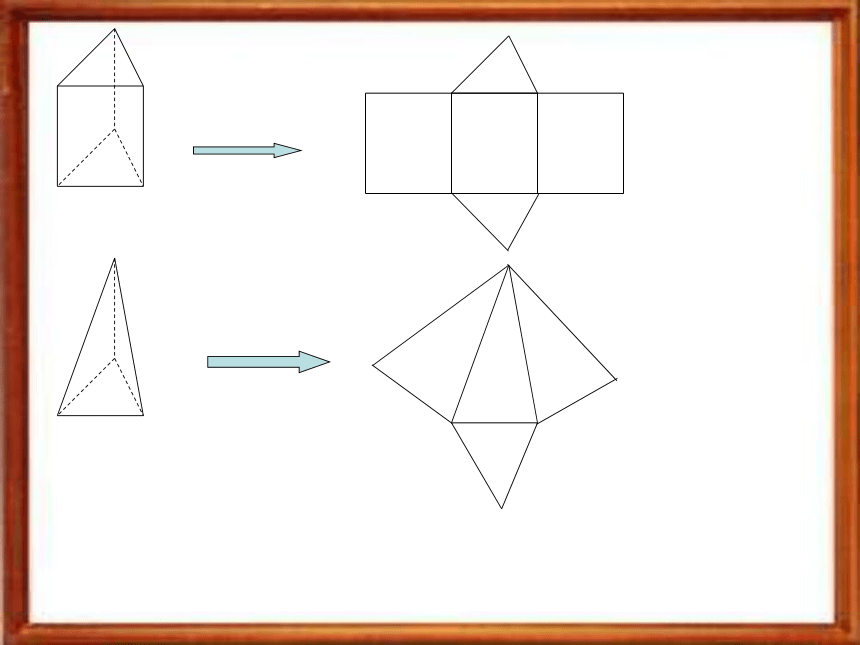
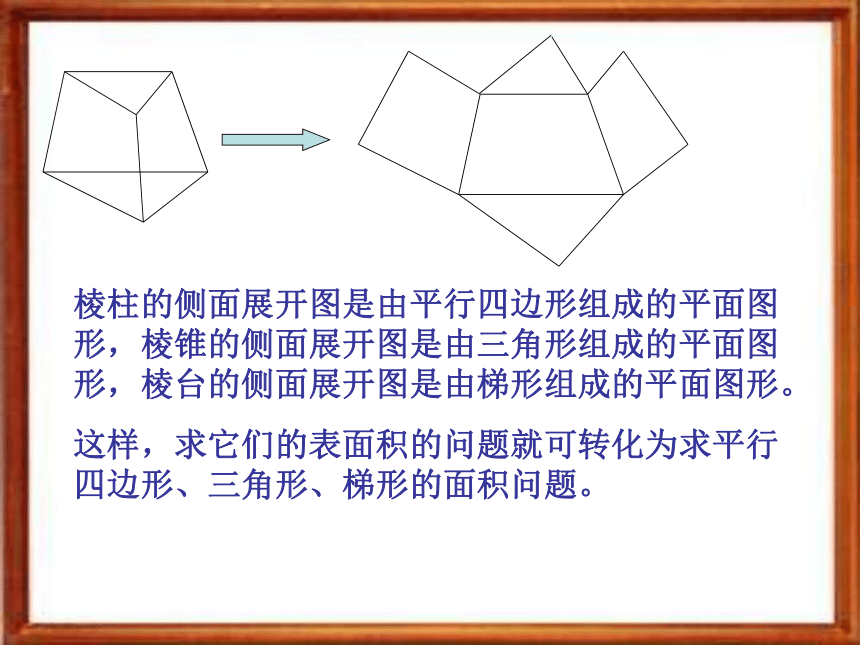
课件20张PPT。1、3 空间几何体的表面积与体积1. 柱体、锥体、台体的表面积正方体、长方体的表面积就是各个面的面积之和。探究 棱柱、棱锥、棱台也是由多个平面图形围成的几何体,它们的展开图是什么?如何计算它们的表面积?棱柱的侧面展开图是由平行四边形组成的平面图形,棱锥的侧面展开图是由三角形组成的平面图形,棱台的侧面展开图是由梯形组成的平面图形。
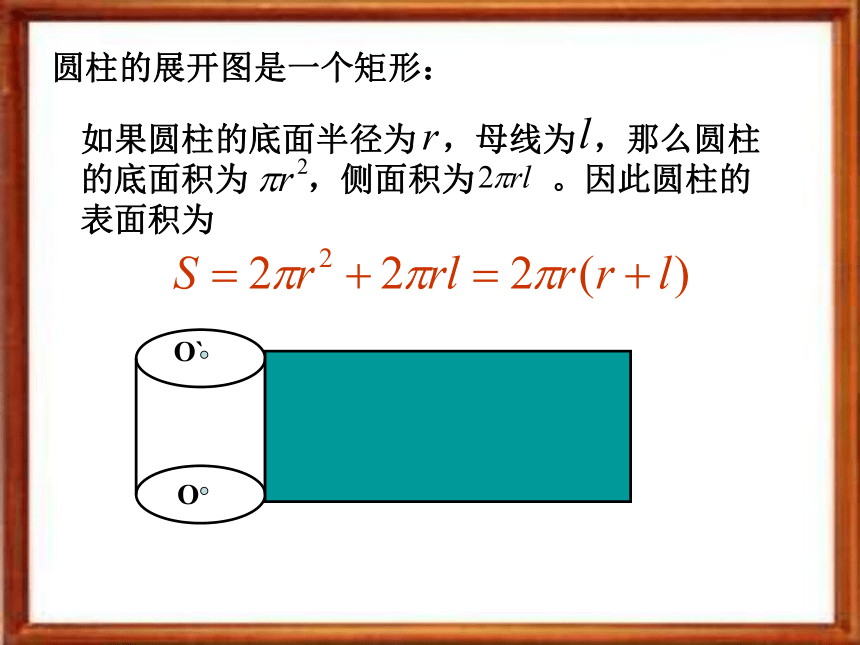
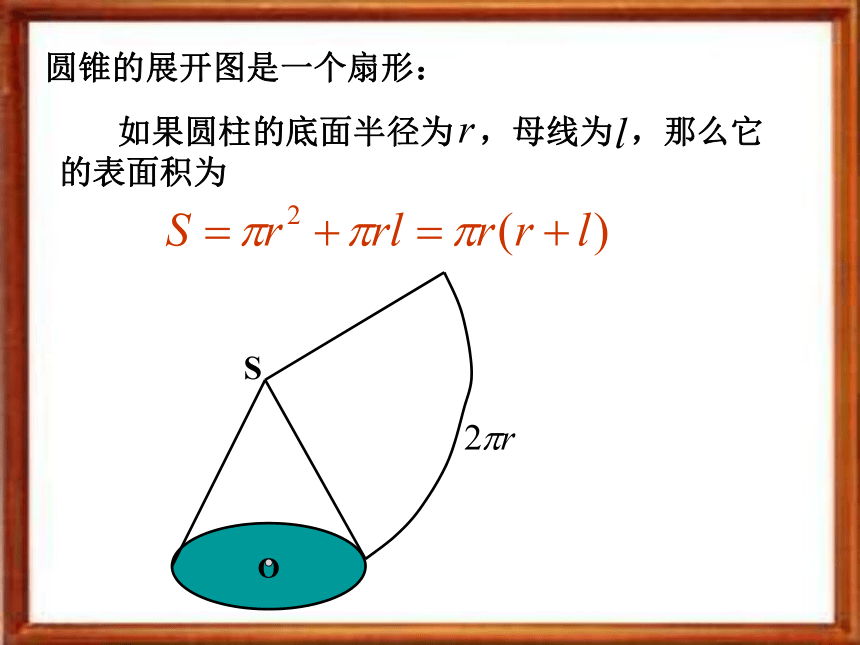
这样,求它们的表面积的问题就可转化为求平行四边形、三角形、梯形的面积问题。D圆柱的展开图是一个矩形:如果圆柱的底面半径为 ,母线为 ,那么圆柱的底面积为 ,侧面积为 。因此圆柱的表面积为圆锥的展开图是一个扇形: 如果圆柱的底面半径为 ,母线为 ,那么它的表面积为设圆台的母线长为l,上、下底面的周长
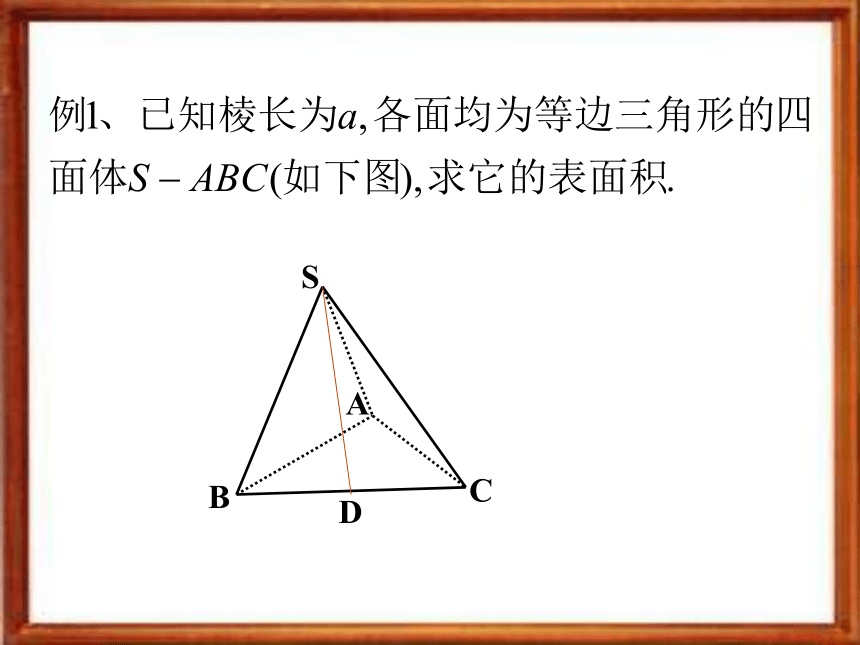
为c/、c,半径分别是r/、r,求圆台的侧面积解:S圆台侧⑴代入⑴,得圆台的展开图是一个扇环,它的表面积等于上、下两个底面和加上侧面的面积,即柱体、锥体、台体的体积正方体、长方体,以及圆柱的体积公式可以统一为:V = Sh(S为底面面积,h为高)一般棱柱的体积公式也是V = Sh,其中S为底面面积,h为高。棱锥的体积公式也是 ,其中S为底面面积,h为高。探究探究棱锥与同底等高的棱柱体积之间的关系?圆台(棱台)的体积公式:其是S‘,S分别为上底面面积,h为圆台(棱台)高。它是同底同高的圆柱的体积的 。圆柱、圆锥、圆台S侧=cl=2πrlS侧= 侧面积=πrlclcllcS侧==π(r+r/)l表面积例4.如图,正方体ABCD-A1B1C1D1的棱长为a,它的各个顶点都在球O的球面上,问球O的表面积。分析:正方体内接于球,则由球和正方体都是中心对称图形可知,它们中心重合,则正方体对角线与球的直径相等。略解:变题1.如果球O和这个正方体的六个面都相切,则有S=——。
变题2.如果球O和这个正方体的各条棱都相切,则有S=——。关键:找正方体的棱长a与球半径R之间的关系例5.钢球直径是5cm,求它的体积.(变式2)把钢球放入一个正方体的有盖纸盒中,至少要用多大的纸?用料最省时,球与正方体有什么位置关系?球内切于正方体侧棱长为5cm1.球的直径伸长为原来的2倍,体积变为原来的几倍?
2.一个正方体的顶点都在球面上,它的棱长是4cm,求这个球的体积. 课堂练习8倍3.有三个球,一球切于正方体的各面,一球切于正方体的各侧棱,一球过正方体的各顶点,求这三个球的体积之比.作轴截面 小结本节课主要介绍了求空间几何体的表面积
和体积的公式和方法:
将空间图形问题转化为平面图形问题,
利用平面图形求面积的方法求立体图形的表面积。
这样,求它们的表面积的问题就可转化为求平行四边形、三角形、梯形的面积问题。D圆柱的展开图是一个矩形:如果圆柱的底面半径为 ,母线为 ,那么圆柱的底面积为 ,侧面积为 。因此圆柱的表面积为圆锥的展开图是一个扇形: 如果圆柱的底面半径为 ,母线为 ,那么它的表面积为设圆台的母线长为l,上、下底面的周长
为c/、c,半径分别是r/、r,求圆台的侧面积解:S圆台侧⑴代入⑴,得圆台的展开图是一个扇环,它的表面积等于上、下两个底面和加上侧面的面积,即柱体、锥体、台体的体积正方体、长方体,以及圆柱的体积公式可以统一为:V = Sh(S为底面面积,h为高)一般棱柱的体积公式也是V = Sh,其中S为底面面积,h为高。棱锥的体积公式也是 ,其中S为底面面积,h为高。探究探究棱锥与同底等高的棱柱体积之间的关系?圆台(棱台)的体积公式:其是S‘,S分别为上底面面积,h为圆台(棱台)高。它是同底同高的圆柱的体积的 。圆柱、圆锥、圆台S侧=cl=2πrlS侧= 侧面积=πrlclcllcS侧==π(r+r/)l表面积例4.如图,正方体ABCD-A1B1C1D1的棱长为a,它的各个顶点都在球O的球面上,问球O的表面积。分析:正方体内接于球,则由球和正方体都是中心对称图形可知,它们中心重合,则正方体对角线与球的直径相等。略解:变题1.如果球O和这个正方体的六个面都相切,则有S=——。
变题2.如果球O和这个正方体的各条棱都相切,则有S=——。关键:找正方体的棱长a与球半径R之间的关系例5.钢球直径是5cm,求它的体积.(变式2)把钢球放入一个正方体的有盖纸盒中,至少要用多大的纸?用料最省时,球与正方体有什么位置关系?球内切于正方体侧棱长为5cm1.球的直径伸长为原来的2倍,体积变为原来的几倍?
2.一个正方体的顶点都在球面上,它的棱长是4cm,求这个球的体积. 课堂练习8倍3.有三个球,一球切于正方体的各面,一球切于正方体的各侧棱,一球过正方体的各顶点,求这三个球的体积之比.作轴截面 小结本节课主要介绍了求空间几何体的表面积
和体积的公式和方法:
将空间图形问题转化为平面图形问题,
利用平面图形求面积的方法求立体图形的表面积。
