2.1.3分层抽样
图片预览







文档简介
课件20张PPT。2.1.3《分层抽样》 湖南省耒阳市振兴学校
高中数学老师欧阳文丰制作
1、知识与技能:
(1)正确理解分层抽样的概念;
(2)掌握分层抽样的一般步骤;
(3)区分简单随机抽样、系统抽样和分层抽样,并选择适当正确的方法进行抽样。
学习目标: 2、过程与方法:通过对现实生活中
实际问题进行分层抽样,感知应用数学
知识解决实际问题的方法。
复习回顾 简单随机抽样、系统抽样的特点是什么?简单随机抽样:①逐个不放回抽取; ②等可能入样;③总体容量较小。
系统抽样:
①分段,按规定的间隔在各部分抽取;
②等可能入样;
③总体容量较大。
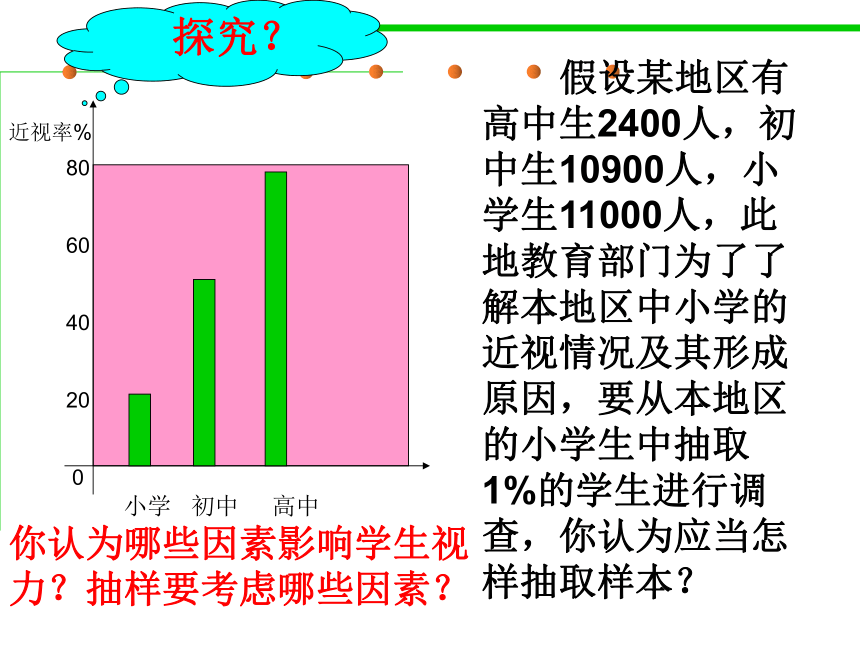
假设某地区有高中生2400人,初中生10900人,小学生11000人,此地教育部门为了了解本地区中小学的近视情况及其形成原因,要从本地区的小学生中抽取1%的学生进行调查,你认为应当怎样抽取样本?你认为哪些因素影响学生视力?抽样要考虑哪些因素?一、分层抽样的定义。 一般地,在抽样时,将总体分成互不交叉的层,然后按照一定的比例,从各层独立地抽取一定数量的个体,将各层取出的个体合在一起作为样本,这种抽样的方法叫分层抽样。应用分层抽样应遵循以下要求:
(1)分层:将相似的个体归入一类,即为一层,分层要求每层的各个个体互不交叉,即遵循不重复、不遗漏的原则。
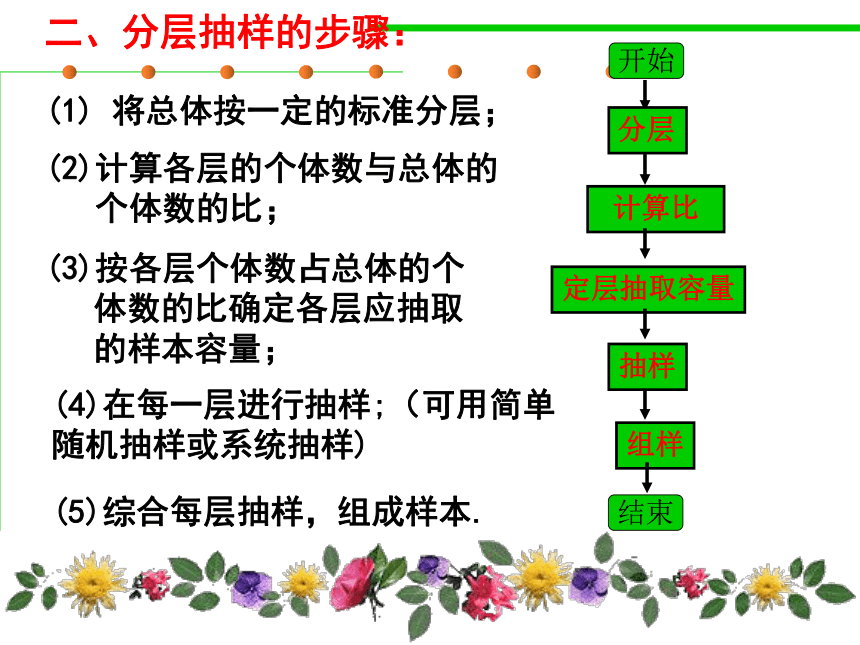
(2)分层抽样为保证每个个体等可能入样,需遵循在各层中进行简单随机抽样,每层样本数量与每层个体数量的比与这层个体数量与总体容量的比相等。二、分层抽样的步骤: (1) 将总体按一定的标准分层;(2)计算各层的个体数与总体的
个体数的比; (3)按各层个体数占总体的个
体数的比确定各层应抽取
的样本容量;(5)综合每层抽样,组成样本.(4)在每一层进行抽样;(可用简单
随机抽样或系统抽样)开始分层计算比定层抽取容量抽样组样结束注意事项: 1.分层抽样法适用于总体中个体差异明显的抽样;
2.分层是按总体中个体的明显差异进行分类;
3.分层抽样是按各层中含个体在总体中所占的比例,确定层抽样的个体个数进行随机抽样.(1)当总体容量较小,样本容量也较小时,制签简单,号签容易搅匀,可采用抽签法(也可采用随机数表法); (2)当总体容量较大,样本容量较小时可用随机数表法;(3)当总体容量较大,样本容量也较大时,可用系统抽样法;(4)当总体由差异明显的几部分组成时,可用分层抽样法。共同特点:均为不放回抽样,在抽样过程中每一个个体被抽取的机会是相等的。课堂练习:1. 在下列问题中,各采用什么抽样方法抽取样本较为合适?(1)从20台彩电中抽取4台进行质量检验;(2)科学会堂有32排座位,每排有40各座位(座位号为01~40),一次报告会坐满了听众,会后为了听取意见,留下了座位号为18的所有的32名听众进行座谈;(3)实验中学有180名教工,其中有专职教师144名,管理人员12名,后勤服务人员24人,今从中抽取一个容量15的样本。简单随机抽样法系统抽样法分层抽样法 2、某单位有老年人27人,中年人55人,青年人81人,为了调查他们的身体情况,需从他们中抽取一个容量为36的样本,则适合的抽取方法是( ) A.简单随机抽样 B.系统抽样
C.分层抽样 D.先从中年人中剔除1人,然后再分层抽样
例1.某高中共有900人,其中高一年级300人,高二年级200人,高三年级400人,现采用分层抽样抽取容量为45的样本,那么高一、高二、高三各年级抽取的人数分别为( )
A.15,5,25 B.15,15,15
C.10,5,30 D.15,10,20D典型例题讲解例2:一个地区共有5个乡镇,人口15万人,其中人口比例为3:2:5:2:3,现从15万人中抽取一个1500人的样本,分析某种疾病的发病率,已知这种疾病与不同的地理位置及水土有关,问应采取什么样的方法?并写出具体过程。解:因为疾病与地理位置和水土均有关系,所以不同乡镇的发病情况差异明显,因而采用分层抽样的方法. 具体过程如下
(1)将15万人分为5层,其中一个乡镇为一层.
(2)按照样本容量的比例求得各乡镇应抽取的人数分别为300人、200人、500人、200人、300 人. (3)按照各层抽取的人数系统抽取各乡镇应抽取的样本.
(4)将1500人组到一起,即得到一个样本。 例3 某电视台在因特网上就观众对某一节目
的喜爱程度进行调查,参加调查的总人数为
12000人,其中持各种态度的人数如表所示电视台为了进一步了解观众的具体想法和意
见,打算从中抽取60人进行更为详细的调查,
应怎样进行抽样?数学应用应取“很喜爱”占“喜爱”占“一般”占“不喜爱”占解:可用分层抽样的方法,其总体容量12000, 人应取 人因此采用分层抽样的方法在很喜爱、喜爱、
一般、不喜爱 的人中各抽取12、23、20、5人。3、某校有老师200人,男学生1200人,女学生1000人,现用分层抽样的方法从所有师生中抽取一个容量为n的样本,已知女学生中抽取的人数为80,则n=1922、某单位有职工160人,其中业务员有104人,管理人员32人,后勤24人,现用分层抽样从中抽取一容量为20的样本,则抽取管理人员( )人
A、3 B、4 C、7 D、12B4、某大学数学系共有本科生5000人,其中一、二、三、四年级的学生比为4:3:2:1,用分层抽样的方法抽取一个容量为200人的样本,则应抽取三年级的学生为( )人。
A、80 B、40 C、60 D、20B课堂练习:抽样过程中每个个体被抽取的可能性相同归纳总结1、分层抽样是当总体由差异明显的几部分组成时采用的抽样方法,进行分层抽样时应注意以下几点:
(1)分层抽样中分多少层、如何分层要视具体情况而定,总的原则是,层内样本的差异要小,面层之间的样本差异要大,且互不重叠。
(2)为了保证每个个体等可能入样,所有层应采用同一抽样比等可能抽样。
(3)在每层抽样时,应采用简单随机抽样或系统抽样的方法进行抽样。
2、分层抽样的优点是:使样本具有较强的代表性,并且抽样过程中可综合选用各种抽样方法,因此分层抽样是一种实用、操作性强、应用比较广泛的抽样方法。
作业
教科书习题2.1第5、6题。 【能力提高】
1.(2004年全国高考天津卷)某工厂生产A、B、C三种不同型号的产品,产品数量之比为2:3:5,现用分层抽样方法抽取一个容量为n的样本,样本中A型产品有16种,那么此样本容量n=_______.80 2、(2004年全国高考湖南卷)某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点,公司为了调查产品销售的情况,需从这600个销售点中抽取一个容量为100的样本,记这项调查为①;在丙地区中有20个特大型销售点,要从中抽取7个调查其销售收入和销后服务等情况,记这项调查为②.则完成①、②这两项调查采用的抽样方法依次是( )A.分层抽样法,系统抽样法B.分层抽样法,简单随机抽样法C.系统抽样法,分层抽样法 D.简单随机抽档法,分层抽样法B
高中数学老师欧阳文丰制作
1、知识与技能:
(1)正确理解分层抽样的概念;
(2)掌握分层抽样的一般步骤;
(3)区分简单随机抽样、系统抽样和分层抽样,并选择适当正确的方法进行抽样。
学习目标: 2、过程与方法:通过对现实生活中
实际问题进行分层抽样,感知应用数学
知识解决实际问题的方法。
复习回顾 简单随机抽样、系统抽样的特点是什么?简单随机抽样:①逐个不放回抽取; ②等可能入样;③总体容量较小。
系统抽样:
①分段,按规定的间隔在各部分抽取;
②等可能入样;
③总体容量较大。
假设某地区有高中生2400人,初中生10900人,小学生11000人,此地教育部门为了了解本地区中小学的近视情况及其形成原因,要从本地区的小学生中抽取1%的学生进行调查,你认为应当怎样抽取样本?你认为哪些因素影响学生视力?抽样要考虑哪些因素?一、分层抽样的定义。 一般地,在抽样时,将总体分成互不交叉的层,然后按照一定的比例,从各层独立地抽取一定数量的个体,将各层取出的个体合在一起作为样本,这种抽样的方法叫分层抽样。应用分层抽样应遵循以下要求:
(1)分层:将相似的个体归入一类,即为一层,分层要求每层的各个个体互不交叉,即遵循不重复、不遗漏的原则。
(2)分层抽样为保证每个个体等可能入样,需遵循在各层中进行简单随机抽样,每层样本数量与每层个体数量的比与这层个体数量与总体容量的比相等。二、分层抽样的步骤: (1) 将总体按一定的标准分层;(2)计算各层的个体数与总体的
个体数的比; (3)按各层个体数占总体的个
体数的比确定各层应抽取
的样本容量;(5)综合每层抽样,组成样本.(4)在每一层进行抽样;(可用简单
随机抽样或系统抽样)开始分层计算比定层抽取容量抽样组样结束注意事项: 1.分层抽样法适用于总体中个体差异明显的抽样;
2.分层是按总体中个体的明显差异进行分类;
3.分层抽样是按各层中含个体在总体中所占的比例,确定层抽样的个体个数进行随机抽样.(1)当总体容量较小,样本容量也较小时,制签简单,号签容易搅匀,可采用抽签法(也可采用随机数表法); (2)当总体容量较大,样本容量较小时可用随机数表法;(3)当总体容量较大,样本容量也较大时,可用系统抽样法;(4)当总体由差异明显的几部分组成时,可用分层抽样法。共同特点:均为不放回抽样,在抽样过程中每一个个体被抽取的机会是相等的。课堂练习:1. 在下列问题中,各采用什么抽样方法抽取样本较为合适?(1)从20台彩电中抽取4台进行质量检验;(2)科学会堂有32排座位,每排有40各座位(座位号为01~40),一次报告会坐满了听众,会后为了听取意见,留下了座位号为18的所有的32名听众进行座谈;(3)实验中学有180名教工,其中有专职教师144名,管理人员12名,后勤服务人员24人,今从中抽取一个容量15的样本。简单随机抽样法系统抽样法分层抽样法 2、某单位有老年人27人,中年人55人,青年人81人,为了调查他们的身体情况,需从他们中抽取一个容量为36的样本,则适合的抽取方法是( ) A.简单随机抽样 B.系统抽样
C.分层抽样 D.先从中年人中剔除1人,然后再分层抽样
例1.某高中共有900人,其中高一年级300人,高二年级200人,高三年级400人,现采用分层抽样抽取容量为45的样本,那么高一、高二、高三各年级抽取的人数分别为( )
A.15,5,25 B.15,15,15
C.10,5,30 D.15,10,20D典型例题讲解例2:一个地区共有5个乡镇,人口15万人,其中人口比例为3:2:5:2:3,现从15万人中抽取一个1500人的样本,分析某种疾病的发病率,已知这种疾病与不同的地理位置及水土有关,问应采取什么样的方法?并写出具体过程。解:因为疾病与地理位置和水土均有关系,所以不同乡镇的发病情况差异明显,因而采用分层抽样的方法. 具体过程如下
(1)将15万人分为5层,其中一个乡镇为一层.
(2)按照样本容量的比例求得各乡镇应抽取的人数分别为300人、200人、500人、200人、300 人. (3)按照各层抽取的人数系统抽取各乡镇应抽取的样本.
(4)将1500人组到一起,即得到一个样本。 例3 某电视台在因特网上就观众对某一节目
的喜爱程度进行调查,参加调查的总人数为
12000人,其中持各种态度的人数如表所示电视台为了进一步了解观众的具体想法和意
见,打算从中抽取60人进行更为详细的调查,
应怎样进行抽样?数学应用应取“很喜爱”占“喜爱”占“一般”占“不喜爱”占解:可用分层抽样的方法,其总体容量12000, 人应取 人因此采用分层抽样的方法在很喜爱、喜爱、
一般、不喜爱 的人中各抽取12、23、20、5人。3、某校有老师200人,男学生1200人,女学生1000人,现用分层抽样的方法从所有师生中抽取一个容量为n的样本,已知女学生中抽取的人数为80,则n=1922、某单位有职工160人,其中业务员有104人,管理人员32人,后勤24人,现用分层抽样从中抽取一容量为20的样本,则抽取管理人员( )人
A、3 B、4 C、7 D、12B4、某大学数学系共有本科生5000人,其中一、二、三、四年级的学生比为4:3:2:1,用分层抽样的方法抽取一个容量为200人的样本,则应抽取三年级的学生为( )人。
A、80 B、40 C、60 D、20B课堂练习:抽样过程中每个个体被抽取的可能性相同归纳总结1、分层抽样是当总体由差异明显的几部分组成时采用的抽样方法,进行分层抽样时应注意以下几点:
(1)分层抽样中分多少层、如何分层要视具体情况而定,总的原则是,层内样本的差异要小,面层之间的样本差异要大,且互不重叠。
(2)为了保证每个个体等可能入样,所有层应采用同一抽样比等可能抽样。
(3)在每层抽样时,应采用简单随机抽样或系统抽样的方法进行抽样。
2、分层抽样的优点是:使样本具有较强的代表性,并且抽样过程中可综合选用各种抽样方法,因此分层抽样是一种实用、操作性强、应用比较广泛的抽样方法。
作业
教科书习题2.1第5、6题。 【能力提高】
1.(2004年全国高考天津卷)某工厂生产A、B、C三种不同型号的产品,产品数量之比为2:3:5,现用分层抽样方法抽取一个容量为n的样本,样本中A型产品有16种,那么此样本容量n=_______.80 2、(2004年全国高考湖南卷)某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点,公司为了调查产品销售的情况,需从这600个销售点中抽取一个容量为100的样本,记这项调查为①;在丙地区中有20个特大型销售点,要从中抽取7个调查其销售收入和销后服务等情况,记这项调查为②.则完成①、②这两项调查采用的抽样方法依次是( )A.分层抽样法,系统抽样法B.分层抽样法,简单随机抽样法C.系统抽样法,分层抽样法 D.简单随机抽档法,分层抽样法B
