2021--2022学年人教版八年级数学下册 17.1.1勾股定理第一课时 课件(共17张PPT)
文档属性
| 名称 | 2021--2022学年人教版八年级数学下册 17.1.1勾股定理第一课时 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 622.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-23 09:52:14 | ||
图片预览




文档简介
(共17张PPT)
17.1.1 勾股定理
新人教版数学八年级下册第十七章 勾股定理
史话勾股定理
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
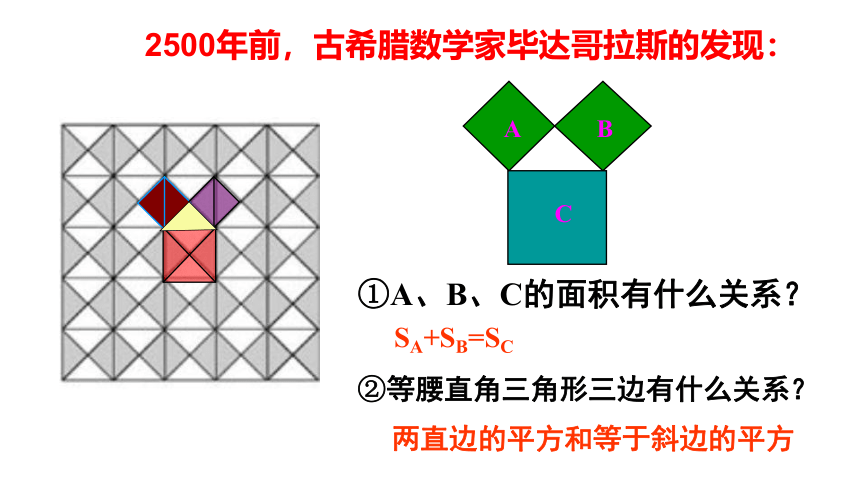
2500年前,古希腊数学家毕达哥拉斯的发现:
①A、B、C的面积有什么关系?
②等腰直角三角形三边有什么关系?
SA+SB=SC
两直边的平方和等于斜边的平方
A
B
C
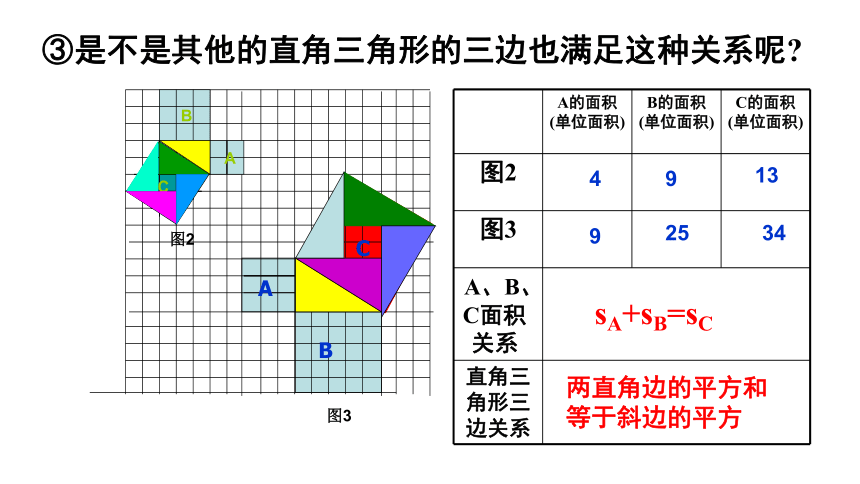
③是不是其他的直角三角形的三边也满足这种关系呢
A
B
C
A的面积(单位面积) B的面积(单位面积) C的面积(单位面积)
图2
图3
A、B、C面积关系
直角三角形三边关系
图2
图3
4
9
13
9
25
34
sA+sB=sC
两直角边的平方和
等于斜边的平方
③是不是其他的直角三角形的三边也满足这种关系呢
A
B
C
证法2:赵爽弦图证法
证法1:欧几里得证法
证法3:美国第二十任总统伽菲尔德的“总统证法”
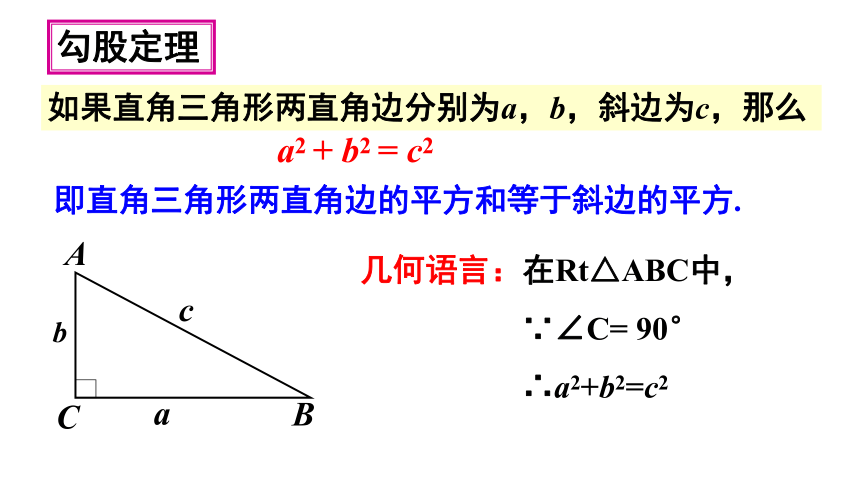
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
即直角三角形两直角边的平方和等于斜边的平方.
勾股定理
几何语言:在Rt△ABC中,
∵∠C= 90°
∴a2+b2=c2
a
b
c
A
C
B
类型之一 勾股定理
例1:已知图17-1-2中的数字代表其所在正方形的面积.
求图中的字母A,B所代表的正方形的面积.
解:正方形A的面积为81+144=225,
正方形B的面积为625-400=225.
点悟:“在直角三角形中,两直角边上的正方形的面积之和等于斜边上的正方形的面积”是勾股定理的图形表现形式.
类型之二 利用勾股定理计算
例2:在△ABC中,∠C=90°,BC=a,AC=b,AB=c.
(1)已知a=1,b=2,求c;
(2)已知a=15,c=17,求b;
(3)已知a= ,b= ,求c;
变式:若一个直角三角形的两边长分别是3、4,则第三边长是 .
4
3
5
A
C
B
3
4
A
C
B
类型之二 利用勾股定理计算
例2:在△ABC中,∠C=90°,BC=a,AC=b,AB=c.
(1)已知a=1,b=2,求c;
(2)已知a=15,c=17,求b;
(3)已知a= ,b= ,求c;
变式:若一个直角三角形的两边长分别是3、4,则第三边长是 .
4
3
5
A
C
B
3
4
A
C
B
类型之二 利用勾股定理计算
例2:在△ABC中,∠C=90°,BC=a,AC=b,AB=c.
(4)已知c=34,a∶b=8∶15,求a,b.
变式1:如图17-1-4,在Rt△ABC中,∠C=90°,∠A=45° ,
则BC∶AC∶AB=_______________;
图17-1-4 图17-1-5
变式2:如图17-1-5,在Rt△ABC中,∠C=90°,∠A=30°,
则BC∶AC∶AB=_______________.
x
x
1
2
变式3:如图,AD是Rt△ABC中BC边上的高.
若AB=6,AC=8,则BC= ,AD= .
10
4.8
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形7的边长为7cm,求正方形1,2,3,4的面积的和.
解:∵ S7= S5+S6 = 49
S5=S1+S2
S6=S3+S4
∴ S1+S2+S3+S4 = S7 = 49cm2
拓展提升
变式:如图,分别以直角三角形的三边为直径作三个半圆S1,S2,S3,这三个半圆的面积之间有什么关系?为什么?
17.1.1 勾股定理
新人教版数学八年级下册第十七章 勾股定理
史话勾股定理
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
2500年前,古希腊数学家毕达哥拉斯的发现:
①A、B、C的面积有什么关系?
②等腰直角三角形三边有什么关系?
SA+SB=SC
两直边的平方和等于斜边的平方
A
B
C
③是不是其他的直角三角形的三边也满足这种关系呢
A
B
C
A的面积(单位面积) B的面积(单位面积) C的面积(单位面积)
图2
图3
A、B、C面积关系
直角三角形三边关系
图2
图3
4
9
13
9
25
34
sA+sB=sC
两直角边的平方和
等于斜边的平方
③是不是其他的直角三角形的三边也满足这种关系呢
A
B
C
证法2:赵爽弦图证法
证法1:欧几里得证法
证法3:美国第二十任总统伽菲尔德的“总统证法”
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
即直角三角形两直角边的平方和等于斜边的平方.
勾股定理
几何语言:在Rt△ABC中,
∵∠C= 90°
∴a2+b2=c2
a
b
c
A
C
B
类型之一 勾股定理
例1:已知图17-1-2中的数字代表其所在正方形的面积.
求图中的字母A,B所代表的正方形的面积.
解:正方形A的面积为81+144=225,
正方形B的面积为625-400=225.
点悟:“在直角三角形中,两直角边上的正方形的面积之和等于斜边上的正方形的面积”是勾股定理的图形表现形式.
类型之二 利用勾股定理计算
例2:在△ABC中,∠C=90°,BC=a,AC=b,AB=c.
(1)已知a=1,b=2,求c;
(2)已知a=15,c=17,求b;
(3)已知a= ,b= ,求c;
变式:若一个直角三角形的两边长分别是3、4,则第三边长是 .
4
3
5
A
C
B
3
4
A
C
B
类型之二 利用勾股定理计算
例2:在△ABC中,∠C=90°,BC=a,AC=b,AB=c.
(1)已知a=1,b=2,求c;
(2)已知a=15,c=17,求b;
(3)已知a= ,b= ,求c;
变式:若一个直角三角形的两边长分别是3、4,则第三边长是 .
4
3
5
A
C
B
3
4
A
C
B
类型之二 利用勾股定理计算
例2:在△ABC中,∠C=90°,BC=a,AC=b,AB=c.
(4)已知c=34,a∶b=8∶15,求a,b.
变式1:如图17-1-4,在Rt△ABC中,∠C=90°,∠A=45° ,
则BC∶AC∶AB=_______________;
图17-1-4 图17-1-5
变式2:如图17-1-5,在Rt△ABC中,∠C=90°,∠A=30°,
则BC∶AC∶AB=_______________.
x
x
1
2
变式3:如图,AD是Rt△ABC中BC边上的高.
若AB=6,AC=8,则BC= ,AD= .
10
4.8
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形7的边长为7cm,求正方形1,2,3,4的面积的和.
解:∵ S7= S5+S6 = 49
S5=S1+S2
S6=S3+S4
∴ S1+S2+S3+S4 = S7 = 49cm2
拓展提升
变式:如图,分别以直角三角形的三边为直径作三个半圆S1,S2,S3,这三个半圆的面积之间有什么关系?为什么?
