2021-2022学年人教版数学八年级下册 18.1.1平行四边形的性质课件 (共14张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册 18.1.1平行四边形的性质课件 (共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 631.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-23 09:59:12 | ||
图片预览



文档简介
(共14张PPT)
平行四边形在生活中无处不在.
情景引入
18.1.1 平行四边形的性质
学练优八年级数学下(RJ)
教学课件
1.两组对边分别平行的四边形叫做平行四边形.
如图:四边形ABCD是平行四边形.记作: ABCD(注意字母顺序)
2.平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
3.平行四边形相对的边称为对边, 相对的角称为对角.
平行四边形的相关概念
A
D
C
B
线段AC、BD就是 ABCD的两条对角线.
对边:AB与CD; BC与DA.
对角: ∠ABC与∠CDA; ∠BAD与∠DCB.
(AB∥CD AD∥BC)
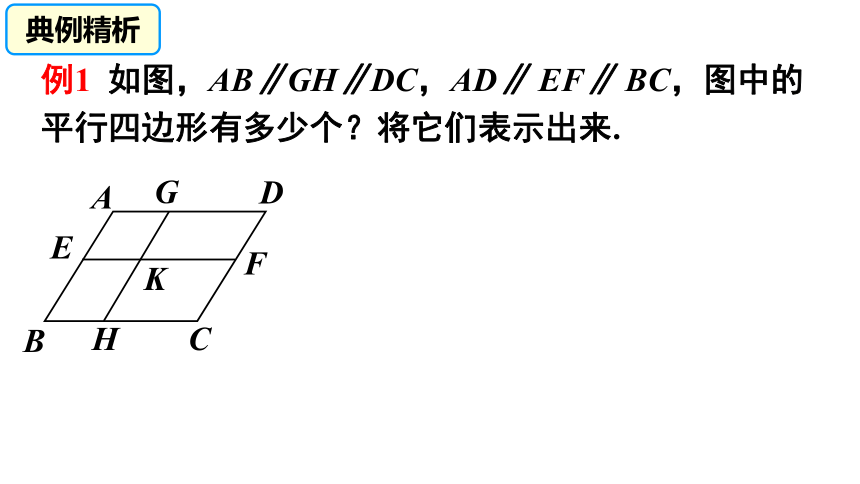
例1 如图,AB∥GH∥DC,AD∥ EF∥ BC,图中的
平行四边形有多少个?将它们表示出来.
D
A
B
C
H
G
F
E
典例精析
K
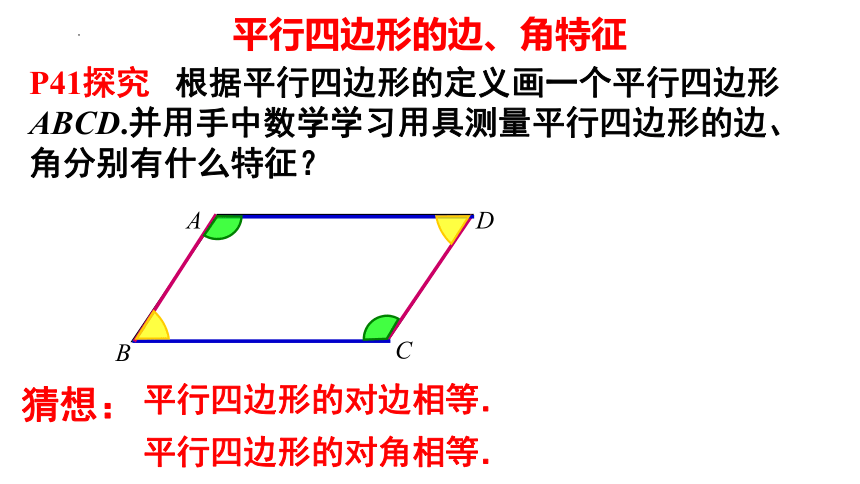
P41探究 根据平行四边形的定义画一个平行四边形ABCD.并用手中数学学习用具测量平行四边形的边、角分别有什么特征?
平行四边形的对边相等.
平行四边形的对角相等.
A
B
C
D
平行四边形的边、角特征
猜想:
A
B
C
D
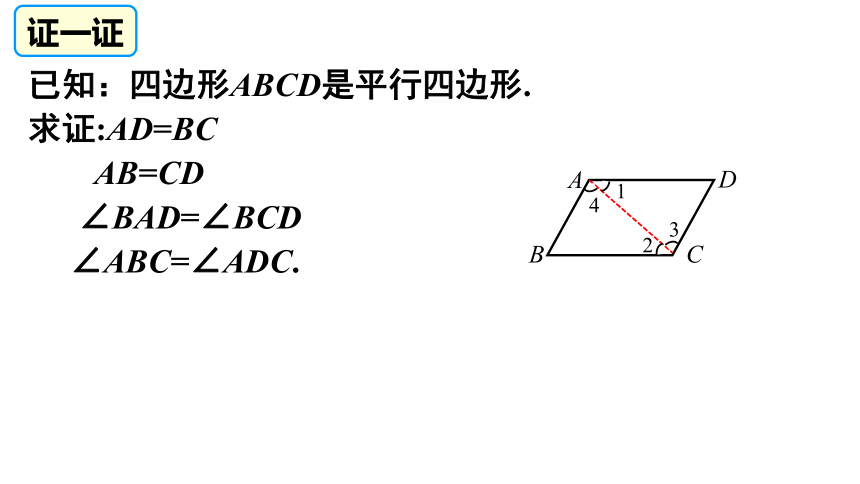
1
4
3
2
已知:四边形ABCD是平行四边形.
求证:AD=BC
AB=CD
∠BAD=∠BCD
∠ABC=∠ADC.
证一证
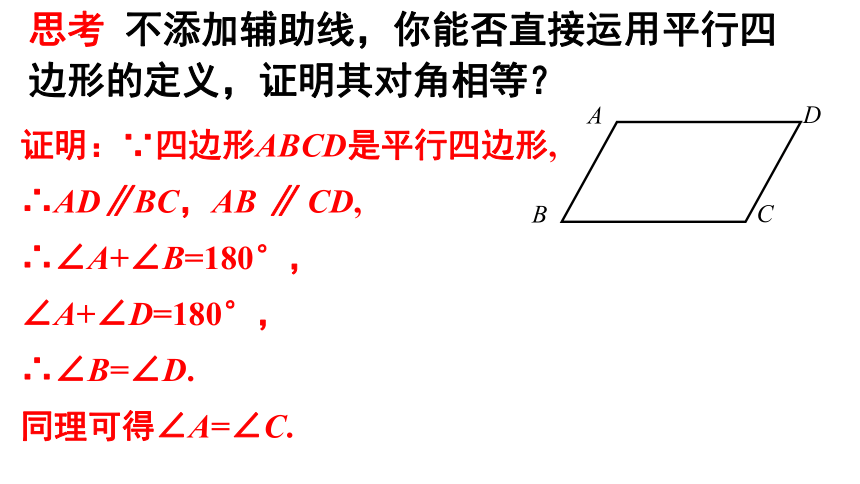
思考 不添加辅助线,你能否直接运用平行四
边形的定义,证明其对角相等?
A
B
C
D
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB ∥ CD,
∴∠A+∠B=180°,
∠A+∠D=180°,
∴∠B=∠D.
同理可得∠A=∠C.
例2 如图,在 ABCD中.
(1)若∠A =38°,求其余三个角的度数;
(2)若AB=3,BC=5,求 ABCD的周长.
A
B
C
D
典例精析
变式训练1 连接AC,已知 ABCD的周长为20 ,
AC=7,求△ABC的周长.
A
B
C
D
变式训练2 在 ABCD中,∠A:∠B=2:3,求各内角的度数.
变式训练3 若 ABCD的周长为28 cm,AB:BC=3:4,求各边的长度.
例3 在 ABCD 中,∠ABC的角平分线BE交AD于
点E,AE=10,ED=4.求 ABCD的周长.
A
B
C
D
E
练习:1.在 ABCD 中,∠ABC的角平分线BE交
AD于点E,∠BCD的角平分线CF交AD于点F.
求证:AE=DF.
A
B
C
D
E
F
2. 在 ABCD 中,∠ABC的角平分线BE交
AD于点E,∠BCD的角平分线CF交AD于点F.
求证:BE⊥ CF.
A
B
C
D
E
F
例4 如图,在 ABCD中,E,F是对角线AC上的两点,并且AE=CF.
求证:BE=DF.
A
D
B
C
E
F
课堂小结
平行
四边形
定义
两组对边分别平行的四边形
性质
两组对边分别平行,相等
两条平行线间的距离相等,
两条平行线间的平行线段也相等
两组对角分别相等,邻角互补
平行四边形在生活中无处不在.
情景引入
18.1.1 平行四边形的性质
学练优八年级数学下(RJ)
教学课件
1.两组对边分别平行的四边形叫做平行四边形.
如图:四边形ABCD是平行四边形.记作: ABCD(注意字母顺序)
2.平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
3.平行四边形相对的边称为对边, 相对的角称为对角.
平行四边形的相关概念
A
D
C
B
线段AC、BD就是 ABCD的两条对角线.
对边:AB与CD; BC与DA.
对角: ∠ABC与∠CDA; ∠BAD与∠DCB.
(AB∥CD AD∥BC)
例1 如图,AB∥GH∥DC,AD∥ EF∥ BC,图中的
平行四边形有多少个?将它们表示出来.
D
A
B
C
H
G
F
E
典例精析
K
P41探究 根据平行四边形的定义画一个平行四边形ABCD.并用手中数学学习用具测量平行四边形的边、角分别有什么特征?
平行四边形的对边相等.
平行四边形的对角相等.
A
B
C
D
平行四边形的边、角特征
猜想:
A
B
C
D
1
4
3
2
已知:四边形ABCD是平行四边形.
求证:AD=BC
AB=CD
∠BAD=∠BCD
∠ABC=∠ADC.
证一证
思考 不添加辅助线,你能否直接运用平行四
边形的定义,证明其对角相等?
A
B
C
D
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB ∥ CD,
∴∠A+∠B=180°,
∠A+∠D=180°,
∴∠B=∠D.
同理可得∠A=∠C.
例2 如图,在 ABCD中.
(1)若∠A =38°,求其余三个角的度数;
(2)若AB=3,BC=5,求 ABCD的周长.
A
B
C
D
典例精析
变式训练1 连接AC,已知 ABCD的周长为20 ,
AC=7,求△ABC的周长.
A
B
C
D
变式训练2 在 ABCD中,∠A:∠B=2:3,求各内角的度数.
变式训练3 若 ABCD的周长为28 cm,AB:BC=3:4,求各边的长度.
例3 在 ABCD 中,∠ABC的角平分线BE交AD于
点E,AE=10,ED=4.求 ABCD的周长.
A
B
C
D
E
练习:1.在 ABCD 中,∠ABC的角平分线BE交
AD于点E,∠BCD的角平分线CF交AD于点F.
求证:AE=DF.
A
B
C
D
E
F
2. 在 ABCD 中,∠ABC的角平分线BE交
AD于点E,∠BCD的角平分线CF交AD于点F.
求证:BE⊥ CF.
A
B
C
D
E
F
例4 如图,在 ABCD中,E,F是对角线AC上的两点,并且AE=CF.
求证:BE=DF.
A
D
B
C
E
F
课堂小结
平行
四边形
定义
两组对边分别平行的四边形
性质
两组对边分别平行,相等
两条平行线间的距离相等,
两条平行线间的平行线段也相等
两组对角分别相等,邻角互补
