2021-2022学年人教版八年级数学下册 18.2.1.1矩形的性质 课件(共18张PPT)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册 18.2.1.1矩形的性质 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 200.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-23 10:50:23 | ||
图片预览


文档简介
(共18张PPT)
18.2.1 矩形
第十八章 平行四边形
第1课时 矩形的性质
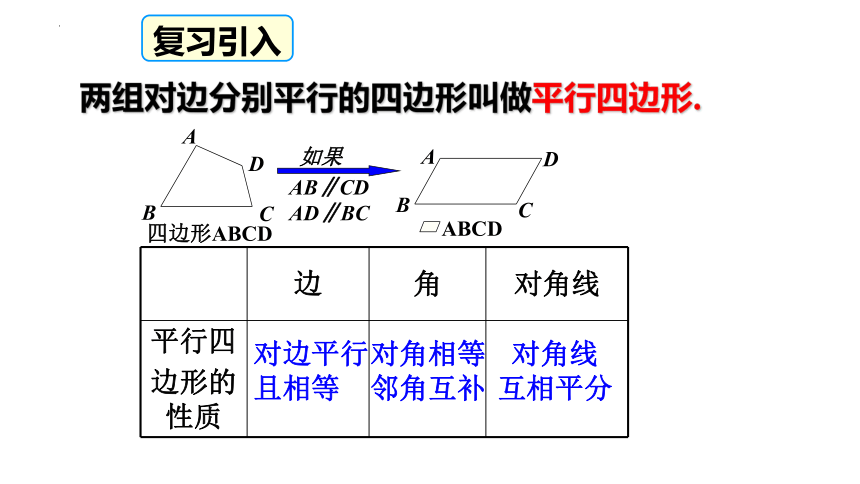
边 角 对角线
平行四 边形的性质
对边平行
且相等
对角相等
邻角互补
对角线
互相平分
两组对边分别平行的四边形叫做平行四边形.
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
ABCD
A
C
复习引入
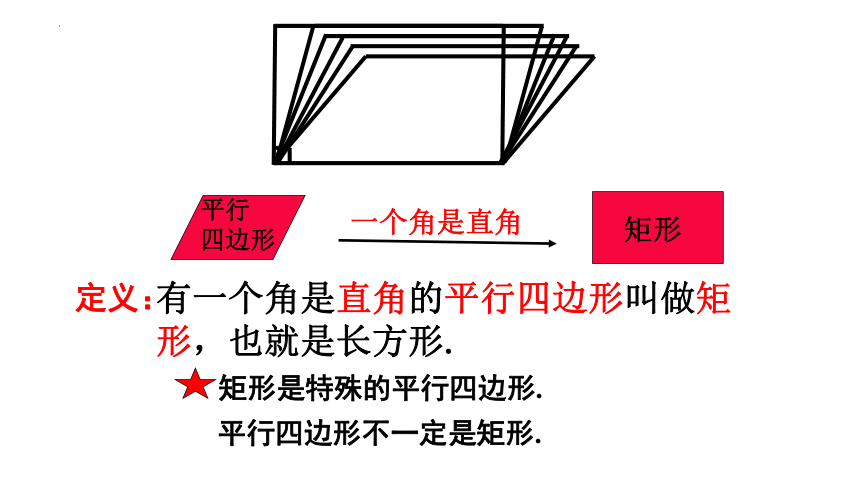
一个角是直角
平行
四边形
矩形
有一个角是直角的平行四边形叫做矩形,也就是长方形.
矩形是特殊的平行四边形.
平行四边形不一定是矩形.
定义:
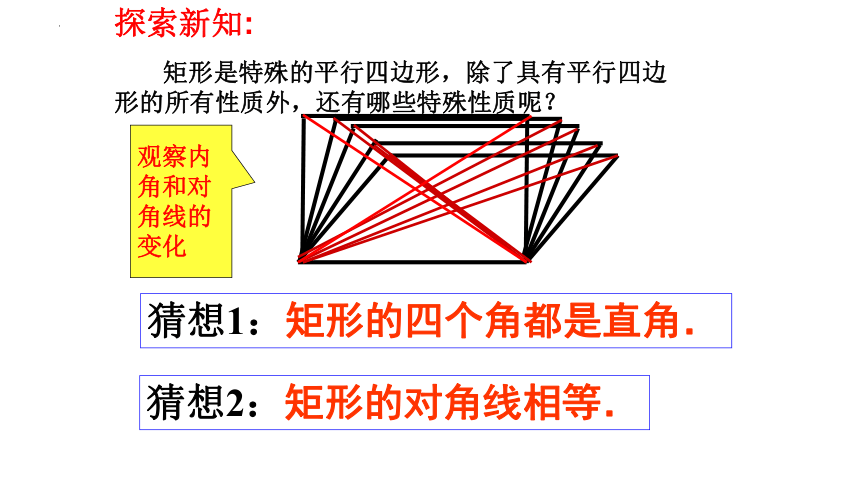
探索新知:
矩形是特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
观察内角和对角线的变化
1:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形,∠B=90°.
求证:∠A=∠B=∠C=∠D=90°.
D
C
B
A
命题
证一证
证明:∵四边形ABCD是矩形,
∴∠D=∠B=90°,∠C=∠A, AB∥DC.
∴∠B+∠C=180°.
又∵∠B = 90°,
∴∠C = 90°.
∴∠B=∠C=∠D=∠A =90°.
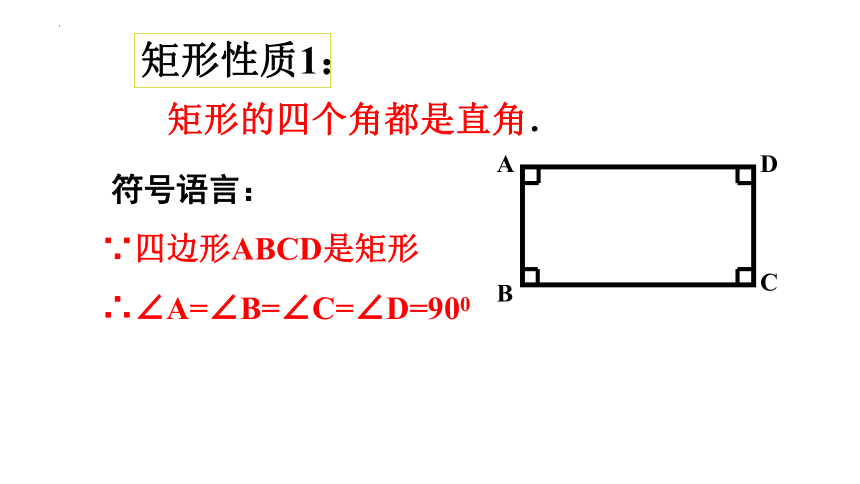
矩形性质1:
A
B
C
D
矩形的四个角都是直角.
∴∠A=∠B=∠C=∠D=900
∵四边形ABCD是矩形
符号语言:
2:矩形的对角线相等..
命题
证一证
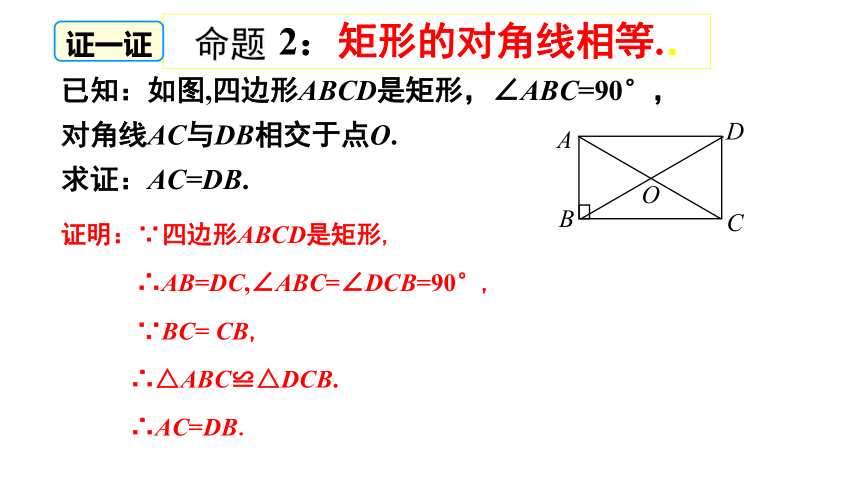
已知:如图,四边形ABCD是矩形,∠ABC=90°,对角线AC与DB相交于点O.
求证:AC=DB.
A
B
C
D
O
证明:∵四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=90°,
∵BC= CB,
∴△ABC≌△DCB.
∴AC=DB.
矩形的对角线相等.
∵四边形ABCD是矩形
∴ AC=BD,
OA=OC,OB=OD
OA=OB=OC=OD
矩形性质2:
A
B
C
D
O
符号语言:
如图,矩形ABCD的对角AC,BD相交于点O,观察图中Rt△ABC,在Rt△ABC中,BO是斜边AC上的中线,BO与AC有什么关系?
根据矩形的性质,可以得到:
直角三角形斜边上的中线等于斜边的一半.
在Rt△ABC中,∵O是斜边AC的中点
∴BO= AC
P53思考
矩形的对称性:
O
2条对称轴
我们都知道矩形是轴对称图形,那么它有几条对称轴?
边 角 对角线 对称性
平行四 边形
矩形
比一比,知关系
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
不一定是轴对称图形
对边平行
且相等
四个角
为直角
对角线互相
平分且相等
轴对称
图形
矩形所特有的性质
如图,四边形ABCD是矩形
1.若AB=8,AD=6,
则AC= _____ ,OB=____.
2.若∠CAB=40°,则∠OCB=____
∠OBA=____ ,∠AOB=_____ ,∠AOD=____.
3.若AC=10,BC=6,则矩形的周长=____,矩形的面积=____.
O
D
C
B
A
练一练
D
C
B
A
┓
4.已知在Rt△ABC中,∠ABC=90°,
BD是斜边AC上的中线.
(1)若BD=3,则AC=______ ;
(2)若∠C=30°,AB=5,则AC=_____,
BD=_____.
练一练
5.如图,在△ABC中,AD是高,
E、F分别是AB、AC的中点.
若AB=10,AC=8,则四边形
AEDF的周长为_____.
例1 如图,矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=4.求矩形对角线的长.
已知矩形的一条对角线长为8,两对角线的一个夹角是120°, 求矩形的边长.
变式:
如果矩形两对角线的夹角是60°或120°,则其中必有等边三角形.
典例精析
A
B
C
D
O
解:∵四边形ABCD是矩形.
∴AC = BD,
OA= OC= AC,OB = OD = BD ,
∴OA = OB.
又∵∠AOB=60°,
∴△OAB是等边三角形,
∴OA=AB=4,
∴AC=BD=2OA=8.
例2 如图,四边形ABCD是矩形,E是AB上一点,且DE=AB,过点C作CF⊥DE,垂足为F.
(1)猜想AD与FC的大小关系;
(2)请证明上面的结论.
例3 如图,在四边形ABCD中,∠ABC=90°,∠ADC=90°,点E为AC的中点,点F为BD的中点,
连接EF.求证:EF⊥BD.
有一个角是直角的平行四边形叫矩形
2.矩形的性质:
对边平行且相等
四个角都是直角
对角线互相平分且相等
1.矩形的定义:
边:
角:
对角线:
4.矩形是轴对称图形.
3.矩形的对角线把矩形分成两对全等的等腰三角形
总结
拓展与应用
如图,在ABCD矩形中AB=6cm,BC=8cm,将矩形折叠,使点B与点D重合,求折痕EF的长.
A
B
O
C
D
E
F
18.2.1 矩形
第十八章 平行四边形
第1课时 矩形的性质
边 角 对角线
平行四 边形的性质
对边平行
且相等
对角相等
邻角互补
对角线
互相平分
两组对边分别平行的四边形叫做平行四边形.
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
ABCD
A
C
复习引入
一个角是直角
平行
四边形
矩形
有一个角是直角的平行四边形叫做矩形,也就是长方形.
矩形是特殊的平行四边形.
平行四边形不一定是矩形.
定义:
探索新知:
矩形是特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
观察内角和对角线的变化
1:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形,∠B=90°.
求证:∠A=∠B=∠C=∠D=90°.
D
C
B
A
命题
证一证
证明:∵四边形ABCD是矩形,
∴∠D=∠B=90°,∠C=∠A, AB∥DC.
∴∠B+∠C=180°.
又∵∠B = 90°,
∴∠C = 90°.
∴∠B=∠C=∠D=∠A =90°.
矩形性质1:
A
B
C
D
矩形的四个角都是直角.
∴∠A=∠B=∠C=∠D=900
∵四边形ABCD是矩形
符号语言:
2:矩形的对角线相等..
命题
证一证
已知:如图,四边形ABCD是矩形,∠ABC=90°,对角线AC与DB相交于点O.
求证:AC=DB.
A
B
C
D
O
证明:∵四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=90°,
∵BC= CB,
∴△ABC≌△DCB.
∴AC=DB.
矩形的对角线相等.
∵四边形ABCD是矩形
∴ AC=BD,
OA=OC,OB=OD
OA=OB=OC=OD
矩形性质2:
A
B
C
D
O
符号语言:
如图,矩形ABCD的对角AC,BD相交于点O,观察图中Rt△ABC,在Rt△ABC中,BO是斜边AC上的中线,BO与AC有什么关系?
根据矩形的性质,可以得到:
直角三角形斜边上的中线等于斜边的一半.
在Rt△ABC中,∵O是斜边AC的中点
∴BO= AC
P53思考
矩形的对称性:
O
2条对称轴
我们都知道矩形是轴对称图形,那么它有几条对称轴?
边 角 对角线 对称性
平行四 边形
矩形
比一比,知关系
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
不一定是轴对称图形
对边平行
且相等
四个角
为直角
对角线互相
平分且相等
轴对称
图形
矩形所特有的性质
如图,四边形ABCD是矩形
1.若AB=8,AD=6,
则AC= _____ ,OB=____.
2.若∠CAB=40°,则∠OCB=____
∠OBA=____ ,∠AOB=_____ ,∠AOD=____.
3.若AC=10,BC=6,则矩形的周长=____,矩形的面积=____.
O
D
C
B
A
练一练
D
C
B
A
┓
4.已知在Rt△ABC中,∠ABC=90°,
BD是斜边AC上的中线.
(1)若BD=3,则AC=______ ;
(2)若∠C=30°,AB=5,则AC=_____,
BD=_____.
练一练
5.如图,在△ABC中,AD是高,
E、F分别是AB、AC的中点.
若AB=10,AC=8,则四边形
AEDF的周长为_____.
例1 如图,矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=4.求矩形对角线的长.
已知矩形的一条对角线长为8,两对角线的一个夹角是120°, 求矩形的边长.
变式:
如果矩形两对角线的夹角是60°或120°,则其中必有等边三角形.
典例精析
A
B
C
D
O
解:∵四边形ABCD是矩形.
∴AC = BD,
OA= OC= AC,OB = OD = BD ,
∴OA = OB.
又∵∠AOB=60°,
∴△OAB是等边三角形,
∴OA=AB=4,
∴AC=BD=2OA=8.
例2 如图,四边形ABCD是矩形,E是AB上一点,且DE=AB,过点C作CF⊥DE,垂足为F.
(1)猜想AD与FC的大小关系;
(2)请证明上面的结论.
例3 如图,在四边形ABCD中,∠ABC=90°,∠ADC=90°,点E为AC的中点,点F为BD的中点,
连接EF.求证:EF⊥BD.
有一个角是直角的平行四边形叫矩形
2.矩形的性质:
对边平行且相等
四个角都是直角
对角线互相平分且相等
1.矩形的定义:
边:
角:
对角线:
4.矩形是轴对称图形.
3.矩形的对角线把矩形分成两对全等的等腰三角形
总结
拓展与应用
如图,在ABCD矩形中AB=6cm,BC=8cm,将矩形折叠,使点B与点D重合,求折痕EF的长.
A
B
O
C
D
E
F
