2021--2022学年沪科版八年级数学下册19.3.8正方形的判定 课件(共18张PPT)
文档属性
| 名称 | 2021--2022学年沪科版八年级数学下册19.3.8正方形的判定 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 264.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-23 10:52:22 | ||
图片预览


文档简介
(共18张PPT)
19.3.8 正方形的判定
课题导入
目标引领
掌握正方形的判定定理,并能利用正方形的判定进行证明或计算.
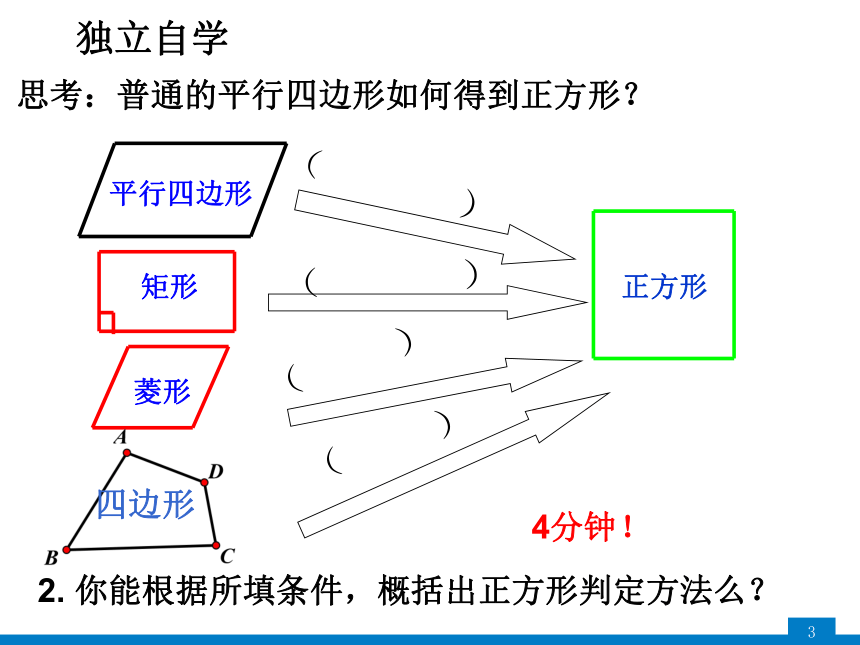
独立自学
菱形
矩形
正方形
平行四边形
( )
( )
( )
2. 你能根据所填条件,概括出正方形判定方法么?
思考:普通的平行四边形如何得到正方形?
( )
四边形
4分钟!
平行四边形
正方形
一组邻边相等
一个角是直角
1、
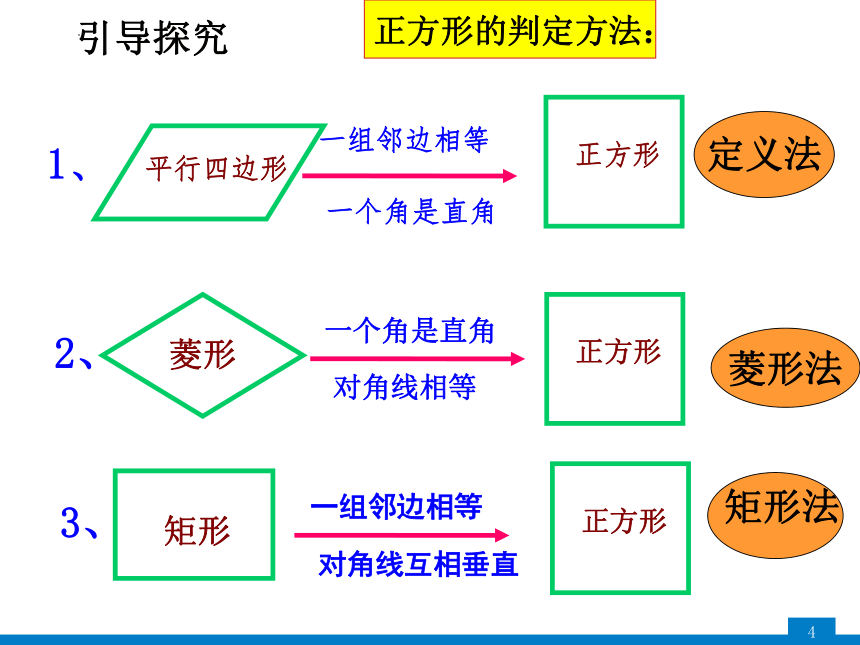
正方形的判定方法:
定义法
菱形法
矩形法
引导探究
正方形
菱形
2、
一个角是直角
对角线相等
矩形
3、
一组邻边相等
正方形
对角线互相垂直
矩形
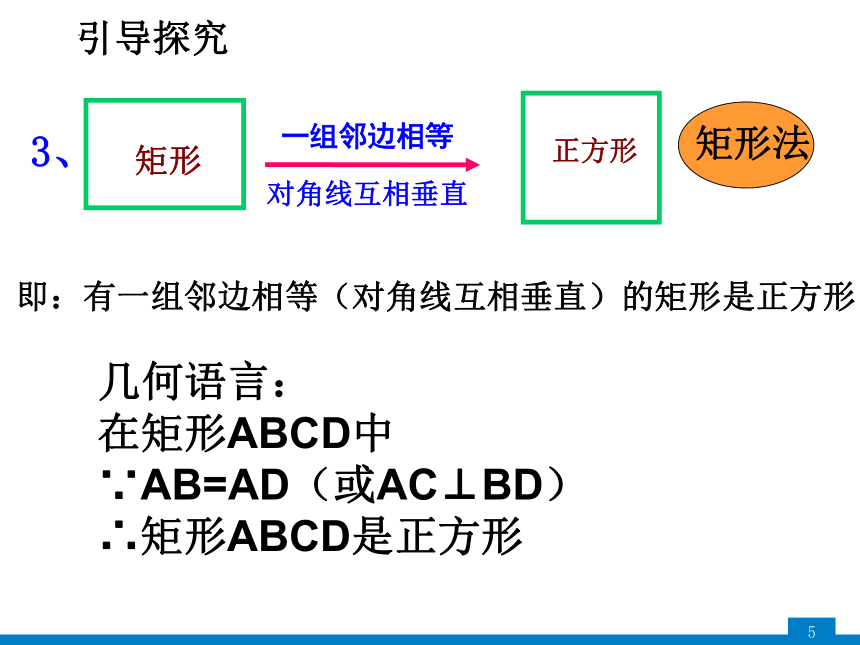
3、
一组邻边相等
正方形
矩形法
引导探究
对角线互相垂直
即:有一组邻边相等(对角线互相垂直)的矩形是正方形
几何语言:
在矩形ABCD中
∵AB=AD(或AC⊥BD)
∴矩形ABCD是正方形
引导探究
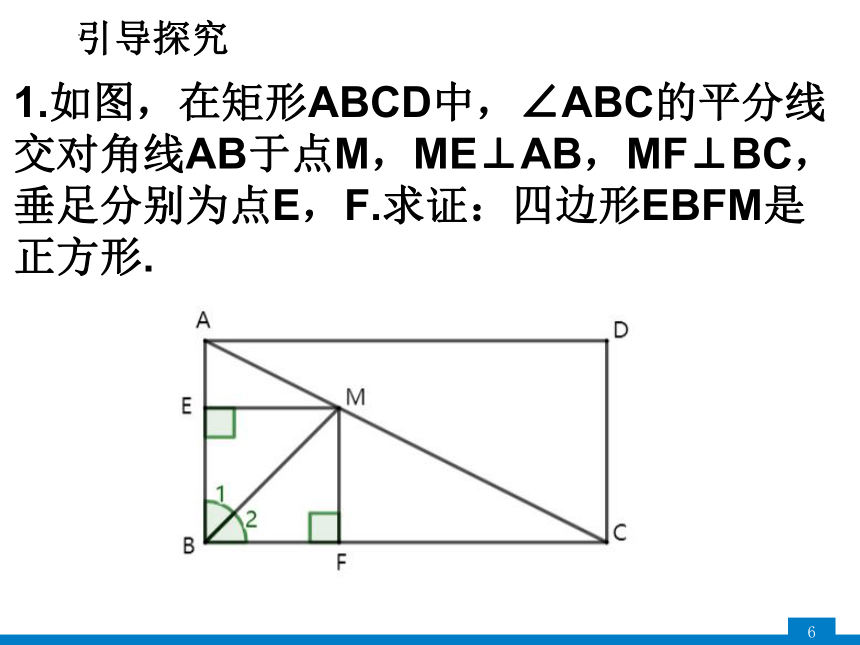
1.如图,在矩形ABCD中,∠ABC的平分线交对角线AB于点M,ME⊥AB,MF⊥BC,垂足分别为点E,F.求证:四边形EBFM是正方形.
引导探究
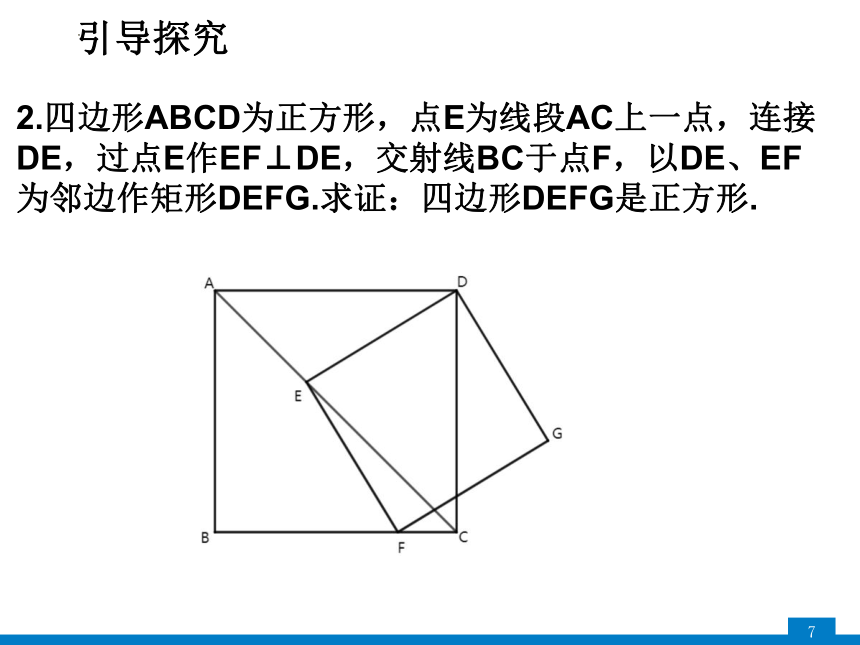
2.四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG.求证:四边形DEFG是正方形.
引导探究
正方形
菱形
2、
一个角是直角
菱形法
即:有一个角是直角(对角线相等)的菱形是正方形
几何语言:
在菱形ABCD中
∵∠A=90°(或AC=BD)
∴菱形ABCD是正方形
对角线相等
引导探究
3.如图,Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,分别过点A,C作AE//DC,CE//AB,两线交于点E.
(1)求证:四边形AECD是菱形;
(2)若∠B=45°,CD=2,求四边形AECD的面积.
引导探究
4.如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD,AB满足什么条件时,四边形MENF是正方形.
引导探究
平行四边形
正方形
一组邻边相等
一个角是直角
1、
定义法
即:有一组邻边相等并且有一个角是直角的平行四边形是正方形
几何语言:
在 ABCD中
∵
∴菱形ABCD是正方形
引导探究
5.判断下列命题哪些是真命题、哪些是假命题?
①对角线相等的菱形是正方形 ( )
②对角线互相垂直的矩形是正方形 ( )
③对角线互相垂直且相等的四边形是正方形 ( )
④四条边都相等的四边形是正方形 ( )
⑤四个角都相等的四边形是正方形 ( )
⑥四边相等,有一个角是直角的四边形是正方形 ( )
真
真
假
假
假
真
引导探究
6.已知Rt△ABC中,CD平分∠ACB,交AB于D,DF//BC,DE//AC,
求证:四边形DECF为正方形.
引导探究
7. 如图,点A',B',C',D'分别是正方形ABCD四条边上的点,并且AA'=BB'=CC'=DD'.
求证:四边形A'B'C'D'是正方形.
引导探究
总结:
你有什么收获或疑惑?
目标升华
如图,在直角三角形中,∠C=90°,∠A、∠B的平分线交于点D.DE⊥AC,DF⊥AB.求证:四边形CEDF为正方形
A
B
C
D
E
F
G
当堂诊学
1、课后练习1、2、3、4;
2、预习
强化补清
19.3.8 正方形的判定
课题导入
目标引领
掌握正方形的判定定理,并能利用正方形的判定进行证明或计算.
独立自学
菱形
矩形
正方形
平行四边形
( )
( )
( )
2. 你能根据所填条件,概括出正方形判定方法么?
思考:普通的平行四边形如何得到正方形?
( )
四边形
4分钟!
平行四边形
正方形
一组邻边相等
一个角是直角
1、
正方形的判定方法:
定义法
菱形法
矩形法
引导探究
正方形
菱形
2、
一个角是直角
对角线相等
矩形
3、
一组邻边相等
正方形
对角线互相垂直
矩形
3、
一组邻边相等
正方形
矩形法
引导探究
对角线互相垂直
即:有一组邻边相等(对角线互相垂直)的矩形是正方形
几何语言:
在矩形ABCD中
∵AB=AD(或AC⊥BD)
∴矩形ABCD是正方形
引导探究
1.如图,在矩形ABCD中,∠ABC的平分线交对角线AB于点M,ME⊥AB,MF⊥BC,垂足分别为点E,F.求证:四边形EBFM是正方形.
引导探究
2.四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG.求证:四边形DEFG是正方形.
引导探究
正方形
菱形
2、
一个角是直角
菱形法
即:有一个角是直角(对角线相等)的菱形是正方形
几何语言:
在菱形ABCD中
∵∠A=90°(或AC=BD)
∴菱形ABCD是正方形
对角线相等
引导探究
3.如图,Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,分别过点A,C作AE//DC,CE//AB,两线交于点E.
(1)求证:四边形AECD是菱形;
(2)若∠B=45°,CD=2,求四边形AECD的面积.
引导探究
4.如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD,AB满足什么条件时,四边形MENF是正方形.
引导探究
平行四边形
正方形
一组邻边相等
一个角是直角
1、
定义法
即:有一组邻边相等并且有一个角是直角的平行四边形是正方形
几何语言:
在 ABCD中
∵
∴菱形ABCD是正方形
引导探究
5.判断下列命题哪些是真命题、哪些是假命题?
①对角线相等的菱形是正方形 ( )
②对角线互相垂直的矩形是正方形 ( )
③对角线互相垂直且相等的四边形是正方形 ( )
④四条边都相等的四边形是正方形 ( )
⑤四个角都相等的四边形是正方形 ( )
⑥四边相等,有一个角是直角的四边形是正方形 ( )
真
真
假
假
假
真
引导探究
6.已知Rt△ABC中,CD平分∠ACB,交AB于D,DF//BC,DE//AC,
求证:四边形DECF为正方形.
引导探究
7. 如图,点A',B',C',D'分别是正方形ABCD四条边上的点,并且AA'=BB'=CC'=DD'.
求证:四边形A'B'C'D'是正方形.
引导探究
总结:
你有什么收获或疑惑?
目标升华
如图,在直角三角形中,∠C=90°,∠A、∠B的平分线交于点D.DE⊥AC,DF⊥AB.求证:四边形CEDF为正方形
A
B
C
D
E
F
G
当堂诊学
1、课后练习1、2、3、4;
2、预习
强化补清
