河南省南阳市2013届高三上学期期终质量评估数学(文)试题
文档属性
| 名称 | 河南省南阳市2013届高三上学期期终质量评估数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 122.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-06 11:18:32 | ||
图片预览



文档简介
南阳市2013届高三年级期终质量评估
数学试题(文)
第Ⅰ卷(选择题共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只 有一项是符合题目要求的.、
1.复数z=的虚部是
A.2 B.2i C.-2i D.-2
2.一个几何体的三视图及其尺寸如右图所示,其中正
(主)视图是直角三角形,侧(左)视图是半圆,
俯视图是等腰三角形,则这个几何体的体积是
(单位cm3)
A.π B.
C. D.
3.设实数x,y满足则x+2y的最小值等于
A.3 B.6 C.9 D.12
4.有下列命题:
①设集合M={x|0<x≤3}, N={x|0<x≤2},则“a∈M”是“a∈N”的充分而不必
要条件;
②命题“若a∈M,则bM”的逆否命题是:若b∈M,则aM;
③若p且q是假命题,则p,q都是假命题;
④命题P:“存在x0∈R, --1>0”的否定P:“任意x∈R,-x-1≤0”
则上述命题中为真命题的是
A.①②③④ B.①③④ C.②④ D.②③④
5.已知公差不为0的等差数列{}满足a1,a3,a4成等比数列,为{}的前n项和,则
的值为
A. B.2
C.3 D.4
6.如图给出的是计算+++……+的值的一个程
序框图,其中判断框内应填入的条件是
A.i>10? B.i<10?
C.i>20? D.i<20?
7.双曲线(a>0,b>0)的离心率是,则的最小值为
A. B.1 C. D.2
8.设A、B、C是圆上不同的三个点,且·=0,存在实数λ,μ使=λ+μ,实数λ,μ的关系为
A. B. C. D.
9.将函数y=f(x)cosx的图像向左平移个单位后,再作关于x轴的对称变换得到函数y=2-1的图像,则f(x)=
A.-2cosx B.2cosx C.-2sinx D.2sinx
10.在三棱锥P-ABC中,AB=BC=,AC=AP=2,PA⊥底面ABC,若P,A,B,C落在以O为球心的球面上,那么球O的体积为
A.8π B. C. D.π
11.已知[x]表示不超过x的最大整数,如: [-0.1]=一1,[0.5]=0,现从[],[],[],[],…,[]中任取一个数,其中该数为奇数的概率为
A. B. C. D.
12.设f(x)是定义在R上的偶函数,对x∈R,都有f(x+4)=f(x),且当x∈[-2,0]时,f(x)=-1,若在区间(-2,6]内关于x的方程f(x)-=0(a>1)恰有3个不同的实数根,则a的取值范围是
A.(1,2) B.(2,+∞) C.(1,) D.(,2)
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题5分,共20分.请把答案填在答题纸相应位置.
13.一支田径队有男女运动员98人,其中男运动员有56人。按男女比例用分层抽样的方 法,从全体运动员中抽出一个容量为28的样本,那么应抽取女运动员人数是____________.
14.已知函数f(x)=则不等式f(x)>0的解集为_____________.
15.设f(x)=+-bx+1的导函数满足=1,=2,其中常数a,b∈R,则曲线y=f(x)在点(1,f(1))处的切线方程为______________.
16.已知斜率为2的直线L过抛物线=px(p>0)的焦点F,且与y轴相交于点A,若
△OAF(O为坐标原点)的面积为l,则P=______________.
三、解答题:本大题共6小题,共70分.应写出必要的文字说明、证明过程或演算步骤.
17.(本题满分10分)
设△ABC的内角A、B、C所对的边分别为a、b、c,已知a=1,b=2,cosC=,
(1)求△ABC的周长;
(2)求cos(A+C)的值.
18.(本题满分12分)
数列{}是等差数列,a1=-2,a3=2.
(1)求通项公式;
(2)若=,求数列{(4+)·}的前n项和.
19.(本题满分12分)
某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x(元)
8
8.2
8.4
8.6
8.8
9
销量y(件)
90
84
83
80
75
68
(1)求回归直线方程y=bx+a,其中b=-20, a=-b;
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4
元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
20.(本题满分12分)
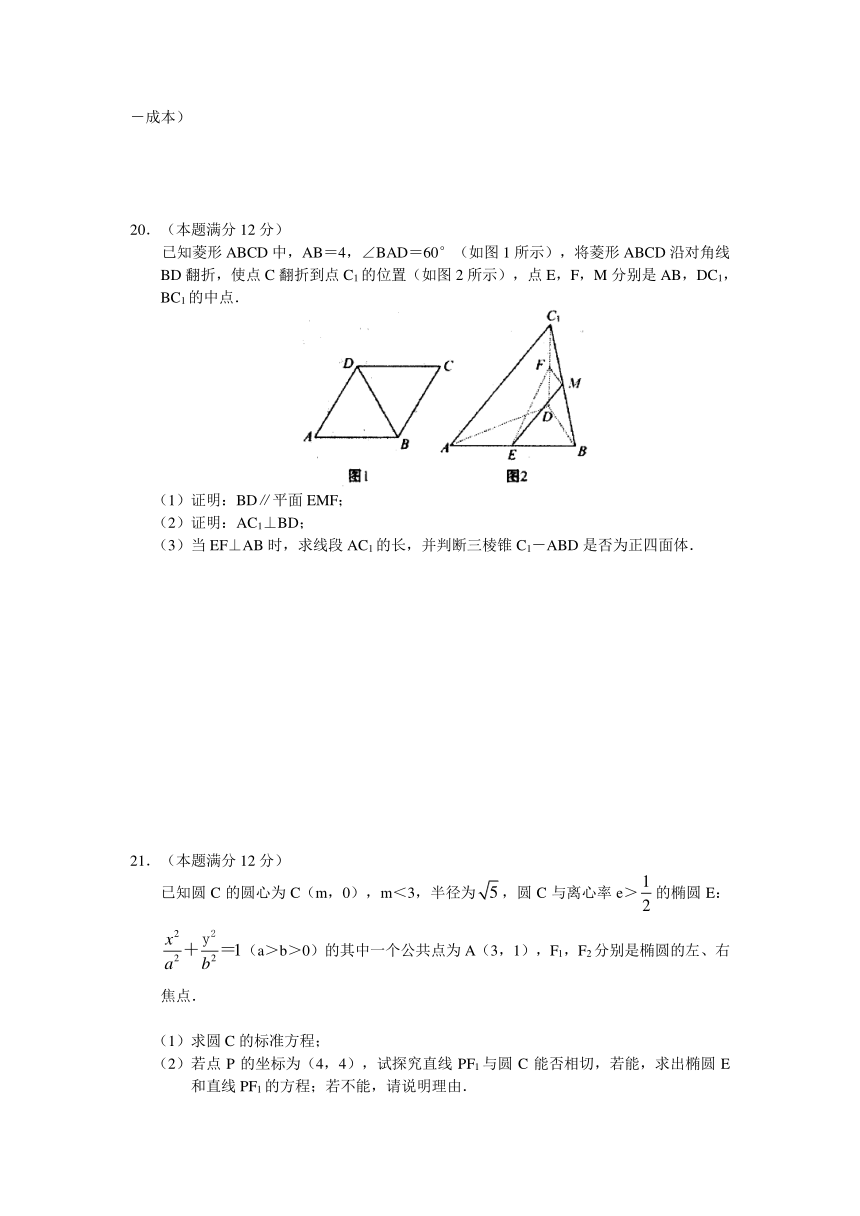
已知菱形ABCD中,AB=4,∠BAD=60°(如图1所示),将菱形ABCD沿对角线BD翻折,使点C翻折到点C1的位置(如图2所示),点E,F,M分别是AB,DC1,BC1的中点.
(1)证明:BD∥平面EMF;
(2)证明:AC1⊥BD;
(3)当EF⊥AB时,求线段AC1的长,并判断三棱锥C1-ABD是否为正四面体.
21.(本题满分12分)
已知圆C的圆心为C(m,0),m<3,半径为,圆C与离心率e>的椭圆E:(a>b>0)的其中一个公共点为A(3,1),F1,F2分别是椭圆的左、右焦点.
(1)求圆C的标准方程;
(2)若点P的坐标为(4,4),试探究直线PF1与圆C能否相切,若能,求出椭圆E和直线PF1的方程;若不能,请说明理由.
22.(本题满分12分)
已知函数f(x)=ln(+a)(a为常数)是实数集R上的奇函数,函数g(x)=
λf(x)+sinx是区间[-1,1]上的减函数.
(1)求a的值;
(2)求关于x的方程=的根的个数;
(3)若g(x)≤+1在x∈[-1,1]上恒成立,求t的取值范围.
数学(文)参考答案
一、选择题:1-5 DBACB 6-10 ACACB 11-12 DD
二、填空题: 13. 12 14. (-1,1) 15. x-y+3=0 16.___4___
三、解答题
17.解:(1)由余弦定理得,c=2,∴△ABC的周长为5. 5分
(2)由(1)得,cos(A+C)=-cosB=-cosC=. 10分
18.解:(1)an=2n-4 6分
(2)
利用错位相减法得, 12分
19.解:(1)由于,
所以,
从而回归直线方程为。 6分
(2)设工厂获得的利润为L元,依题意得
当且仅当时,L取得最大值。
故当单价定为8.25元时,工厂可获得最大利润。 12分
20.证明:(1)因为点F,M分别是C1D,C1B的中点,
所以FM∥BD.
又FM?平面EMF,BD平面EMF,
所以BD∥平面EMF. 4分
(2)在菱形ABCD中,设O为AC,BD的交点,
则AC⊥BD.
所以在三棱锥C1-ABD中,C1O⊥BD,AO⊥BD.
又C1O∩AO=O,
所以BD⊥平面AOC1,
又AC1?平面AOC1,所以BD⊥AC1. 8分
(3)连接DE,C1E,在菱形ABCD中,DA=AB,∠BAD=60°,
所以△ABD是等边三角形.
所以DA=DB.
因为E为AB中点,所以DE⊥AB.
又EF⊥AB,EF∩DE=E,
所以AB⊥平面DEF,即AB⊥平面DEC1.
又C1E?平面DEC1,
所以AB⊥C1E.
因为AE=EB,AB=4,BC1=AB,
所以AC1=BC1=4. 11分
由此知,三棱锥是正四面体。 12分
21. 解:(1)由已知可设圆C的方程为,
将点A的坐标代入圆C的方程,得.
即,解得,
∵, ∴.
∴圆C的方程为. ……4分
(2)直线能与圆C相切,
依题意设直线的方程为,即,
若直线与圆C相切,则.
∴,解得. ……7分
当时,直线与x轴的交点横坐标为,不合题意,舍去.
当时,直线与x轴的交点横坐标为,
∴.
∴由椭圆的定义得:
,
∴, ∴ ,故直线能与圆相切.……10分
直线的方程为,椭圆E的方程为. ………12分
22.解:(1)是奇函数,则恒成立.
即 2分
(2)由(1)知
令,
,
当上为增函数;
上为减函数,
当时,
而,
∴只有一个根. 6分
(3)又在[-1,1]上单调递减,
且∴
令则
. 12分
数学试题(文)
第Ⅰ卷(选择题共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只 有一项是符合题目要求的.、
1.复数z=的虚部是
A.2 B.2i C.-2i D.-2
2.一个几何体的三视图及其尺寸如右图所示,其中正
(主)视图是直角三角形,侧(左)视图是半圆,
俯视图是等腰三角形,则这个几何体的体积是
(单位cm3)
A.π B.
C. D.
3.设实数x,y满足则x+2y的最小值等于
A.3 B.6 C.9 D.12
4.有下列命题:
①设集合M={x|0<x≤3}, N={x|0<x≤2},则“a∈M”是“a∈N”的充分而不必
要条件;
②命题“若a∈M,则bM”的逆否命题是:若b∈M,则aM;
③若p且q是假命题,则p,q都是假命题;
④命题P:“存在x0∈R, --1>0”的否定P:“任意x∈R,-x-1≤0”
则上述命题中为真命题的是
A.①②③④ B.①③④ C.②④ D.②③④
5.已知公差不为0的等差数列{}满足a1,a3,a4成等比数列,为{}的前n项和,则
的值为
A. B.2
C.3 D.4
6.如图给出的是计算+++……+的值的一个程
序框图,其中判断框内应填入的条件是
A.i>10? B.i<10?
C.i>20? D.i<20?
7.双曲线(a>0,b>0)的离心率是,则的最小值为
A. B.1 C. D.2
8.设A、B、C是圆上不同的三个点,且·=0,存在实数λ,μ使=λ+μ,实数λ,μ的关系为
A. B. C. D.
9.将函数y=f(x)cosx的图像向左平移个单位后,再作关于x轴的对称变换得到函数y=2-1的图像,则f(x)=
A.-2cosx B.2cosx C.-2sinx D.2sinx
10.在三棱锥P-ABC中,AB=BC=,AC=AP=2,PA⊥底面ABC,若P,A,B,C落在以O为球心的球面上,那么球O的体积为
A.8π B. C. D.π
11.已知[x]表示不超过x的最大整数,如: [-0.1]=一1,[0.5]=0,现从[],[],[],[],…,[]中任取一个数,其中该数为奇数的概率为
A. B. C. D.
12.设f(x)是定义在R上的偶函数,对x∈R,都有f(x+4)=f(x),且当x∈[-2,0]时,f(x)=-1,若在区间(-2,6]内关于x的方程f(x)-=0(a>1)恰有3个不同的实数根,则a的取值范围是
A.(1,2) B.(2,+∞) C.(1,) D.(,2)
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题5分,共20分.请把答案填在答题纸相应位置.
13.一支田径队有男女运动员98人,其中男运动员有56人。按男女比例用分层抽样的方 法,从全体运动员中抽出一个容量为28的样本,那么应抽取女运动员人数是____________.
14.已知函数f(x)=则不等式f(x)>0的解集为_____________.
15.设f(x)=+-bx+1的导函数满足=1,=2,其中常数a,b∈R,则曲线y=f(x)在点(1,f(1))处的切线方程为______________.
16.已知斜率为2的直线L过抛物线=px(p>0)的焦点F,且与y轴相交于点A,若
△OAF(O为坐标原点)的面积为l,则P=______________.
三、解答题:本大题共6小题,共70分.应写出必要的文字说明、证明过程或演算步骤.
17.(本题满分10分)
设△ABC的内角A、B、C所对的边分别为a、b、c,已知a=1,b=2,cosC=,
(1)求△ABC的周长;
(2)求cos(A+C)的值.
18.(本题满分12分)
数列{}是等差数列,a1=-2,a3=2.
(1)求通项公式;
(2)若=,求数列{(4+)·}的前n项和.
19.(本题满分12分)
某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x(元)
8
8.2
8.4
8.6
8.8
9
销量y(件)
90
84
83
80
75
68
(1)求回归直线方程y=bx+a,其中b=-20, a=-b;
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4
元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
20.(本题满分12分)
已知菱形ABCD中,AB=4,∠BAD=60°(如图1所示),将菱形ABCD沿对角线BD翻折,使点C翻折到点C1的位置(如图2所示),点E,F,M分别是AB,DC1,BC1的中点.
(1)证明:BD∥平面EMF;
(2)证明:AC1⊥BD;
(3)当EF⊥AB时,求线段AC1的长,并判断三棱锥C1-ABD是否为正四面体.
21.(本题满分12分)
已知圆C的圆心为C(m,0),m<3,半径为,圆C与离心率e>的椭圆E:(a>b>0)的其中一个公共点为A(3,1),F1,F2分别是椭圆的左、右焦点.
(1)求圆C的标准方程;
(2)若点P的坐标为(4,4),试探究直线PF1与圆C能否相切,若能,求出椭圆E和直线PF1的方程;若不能,请说明理由.
22.(本题满分12分)
已知函数f(x)=ln(+a)(a为常数)是实数集R上的奇函数,函数g(x)=
λf(x)+sinx是区间[-1,1]上的减函数.
(1)求a的值;
(2)求关于x的方程=的根的个数;
(3)若g(x)≤+1在x∈[-1,1]上恒成立,求t的取值范围.
数学(文)参考答案
一、选择题:1-5 DBACB 6-10 ACACB 11-12 DD
二、填空题: 13. 12 14. (-1,1) 15. x-y+3=0 16.___4___
三、解答题
17.解:(1)由余弦定理得,c=2,∴△ABC的周长为5. 5分
(2)由(1)得,cos(A+C)=-cosB=-cosC=. 10分
18.解:(1)an=2n-4 6分
(2)
利用错位相减法得, 12分
19.解:(1)由于,
所以,
从而回归直线方程为。 6分
(2)设工厂获得的利润为L元,依题意得
当且仅当时,L取得最大值。
故当单价定为8.25元时,工厂可获得最大利润。 12分
20.证明:(1)因为点F,M分别是C1D,C1B的中点,
所以FM∥BD.
又FM?平面EMF,BD平面EMF,
所以BD∥平面EMF. 4分
(2)在菱形ABCD中,设O为AC,BD的交点,
则AC⊥BD.
所以在三棱锥C1-ABD中,C1O⊥BD,AO⊥BD.
又C1O∩AO=O,
所以BD⊥平面AOC1,
又AC1?平面AOC1,所以BD⊥AC1. 8分
(3)连接DE,C1E,在菱形ABCD中,DA=AB,∠BAD=60°,
所以△ABD是等边三角形.
所以DA=DB.
因为E为AB中点,所以DE⊥AB.
又EF⊥AB,EF∩DE=E,
所以AB⊥平面DEF,即AB⊥平面DEC1.
又C1E?平面DEC1,
所以AB⊥C1E.
因为AE=EB,AB=4,BC1=AB,
所以AC1=BC1=4. 11分
由此知,三棱锥是正四面体。 12分
21. 解:(1)由已知可设圆C的方程为,
将点A的坐标代入圆C的方程,得.
即,解得,
∵, ∴.
∴圆C的方程为. ……4分
(2)直线能与圆C相切,
依题意设直线的方程为,即,
若直线与圆C相切,则.
∴,解得. ……7分
当时,直线与x轴的交点横坐标为,不合题意,舍去.
当时,直线与x轴的交点横坐标为,
∴.
∴由椭圆的定义得:
,
∴, ∴ ,故直线能与圆相切.……10分
直线的方程为,椭圆E的方程为. ………12分
22.解:(1)是奇函数,则恒成立.
即 2分
(2)由(1)知
令,
,
当上为增函数;
上为减函数,
当时,
而,
∴只有一个根. 6分
(3)又在[-1,1]上单调递减,
且∴
令则
. 12分
同课章节目录
