湖南省澧县张公庙中学2021-2022学年下期湘教版八年级数学期中复习试卷(word版含答案)
文档属性
| 名称 | 湖南省澧县张公庙中学2021-2022学年下期湘教版八年级数学期中复习试卷(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 905.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-23 15:10:16 | ||
图片预览



文档简介
湖南省澧县张公庙中学2021-2022学年湘教版八年级数学下册期中复习试卷(一)
一.选择题(共10小题,每小题3分,共30分)
1.已知,如果以,的长为直角边作一个直角三角形,那么这个直角三角形的斜边长为
A. B.5 C. D.
2.如图, 直线,,表示三条公路 . 现要建造一个中转站,使到三条公路的距离都相等, 则中转站可选择的点有
A . 一处 B . 二处 C . 三处 D . 四处
3.下列关于平行四边形性质叙述正确的个数是
①平行四边形的对边平行,②平行四边形的对边相等,③平行四边形的对角相等,④平行四边形的对角线相等.
A.1 B.2 C.3 D.4
4.下列疫情防控标识图案中,是中心对称图形的是
A. B. C. D.
5.如图,,于,于,,交于,则以下结论:①;②;③点在的平分线上.正确的是
A.① B.② C.①② D.①②③
6.下列各点中,关于原点对称的两个点是
A.与 B.与
C.与 D.与
7.如图,平行四边形中,是上一点,、分别是、的平分线,若,,则平行四边形的面积为
A.96 B.48 C.60 D.30
8.小玲的爸爸在制作平行四边形框架时,采用了一种方法:如图所示,将两根木条,的中点重叠,并用钉子固定,则四边形就是平行四边形,这种方法的依据是
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对边分别平行的四边形是平行四边形
9.如图,是棋盘的一部分,建立适当的平面直角坐标系,已知棋子“车”的坐标为,棋子“炮”的坐标为,则棋子“马”的坐标为
A. B. C. D.
10.已知等腰中,于点,且,则底角的度数为
A. B. C. D.,或
二.填空题(共8小题,每小题3分,共24分)
11.如图,在中,,将折叠,使点落在边上的点处,折痕为;若,则 .
12.如图,直线、垂直相交于点,曲线关于点成中心对称,点的对称点是点,于点,于点.若,,则阴影部分的面积之和为 .
13.已知在中,,点、分别是、的中点,连接,在上有一点,,连接,,若,则 .
14.在平面直角坐标系中,若点在轴上,则的值是 .
15.平行四边形的对角线与相交于点,且,请添加一个条件: ,使得平行四边形为正方形.
16.已知平面直角坐标系内不同的两点和到轴的距离相等,则的值为 .
17.菱形的周长为,对角线和相交于点,,则菱形的面积为 .
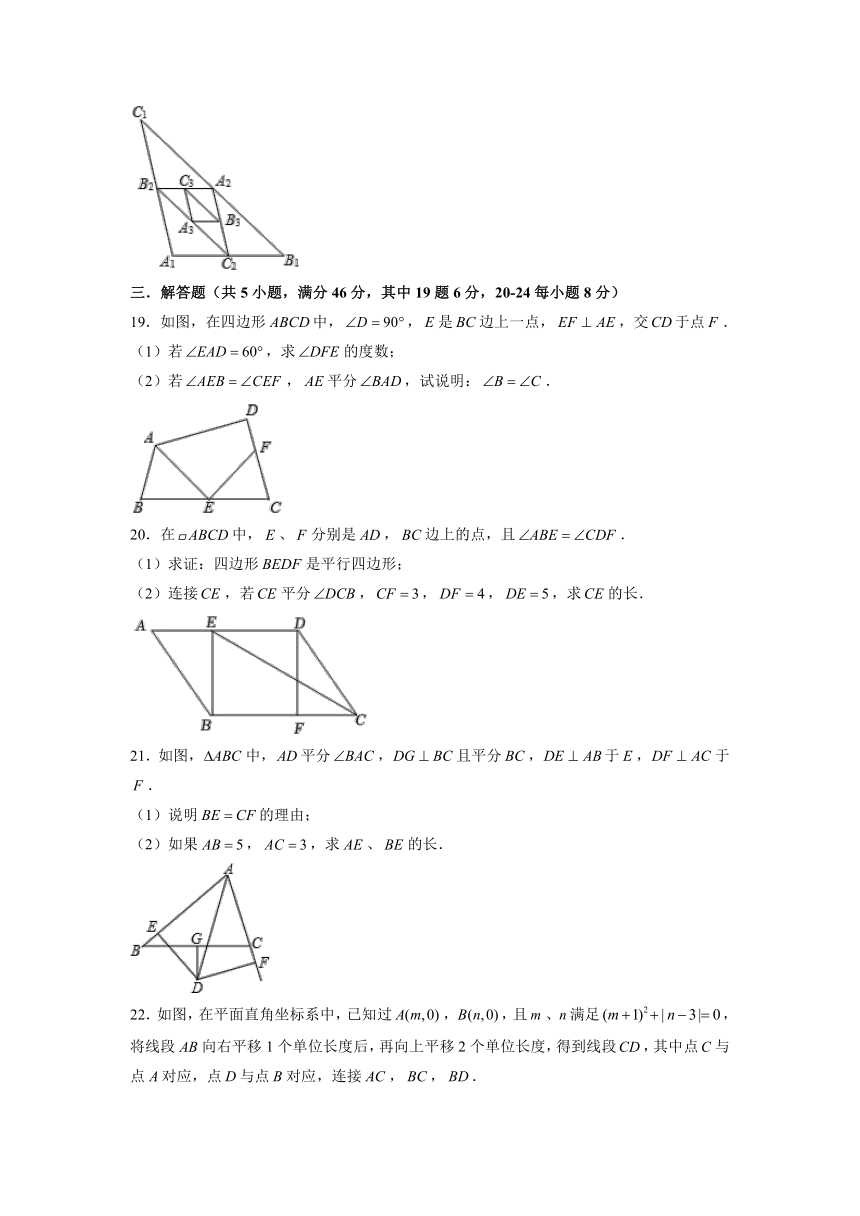
18.如图,△中,,,.点,,分别是边,,的中点;点,,分别是边,,的中点;以此类推,则△的周长是 .
三.解答题(共5小题,满分46分,其中19题6分,20-24每小题8分)
19.如图,在四边形中,,是边上一点,,交于点.
(1)若,求的度数;
(2)若,平分,试说明:.
20.在中,、分别是,边上的点,且.
(1)求证:四边形是平行四边形;
(2)连接,若平分,,,,求的长.
21.如图,中,平分,且平分,于,于.
(1)说明的理由;
(2)如果,,求、的长.
22.如图,在平面直角坐标系中,已知过,,且、满足,将线段向右平移1个单位长度后,再向上平移2个单位长度,得到线段,其中点与点对应,点与点对应,连接,,.
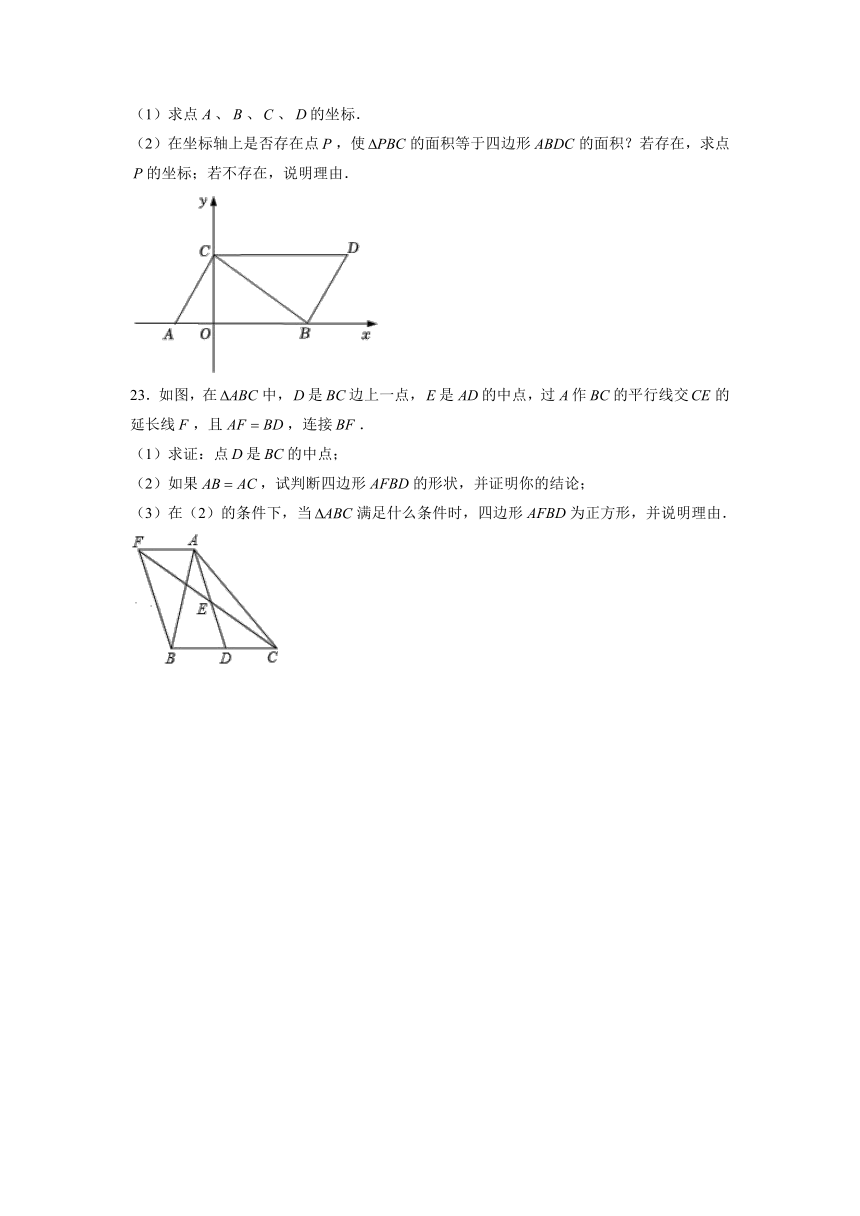
(1)求点、、、的坐标.
(2)在坐标轴上是否存在点,使的面积等于四边形的面积?若存在,求点的坐标;若不存在,说明理由.
23.如图,在中,是边上一点,是的中点,过作的平行线交的延长线,且,连接.
(1)求证:点是的中点;
(2)如果,试判断四边形的形状,并证明你的结论;
(3)在(2)的条件下,当满足什么条件时,四边形为正方形,并说明理由.
湖南省澧县张公庙中学2021-2022学年湘教版八年级数学下册期中复习试卷(一)参考简答
一.选择题(共10小题)
1.. 2.. 3.. 4.. 5.. 6.. 7.. 8..
9.. 10..
二.填空题(共8小题)
11. 39 . 12. 12 . 13. . 14. .
15. 或 . 16. 1或 . 17. 4 .
18. .
三.解答题(共5小题)
19.如图,在四边形中,,是边上一点,,交于点.
(1)若,求的度数;
(2)若,平分,试说明:.
【解】:(1),
,
四边形的内角和是,
,,
;
(2)证明:四边形的内角和是,,,
,
,
,
平分,
,
,
,,,
.
20.在中,、分别是,边上的点,且.
(1)求证:四边形是平行四边形;
(2)连接,若平分,,,,求的长.
【解】:(1)证明:四边形是平行四边形,
,,,,
,
,
,
,
,
四边形是平行四边形;
(2)四边形是平行四边形,
,,
四边形是平行四边形,
,
,
平分,
,
,
,
在中,,,,
,
是直角三角形,
,
,
在中,.
21.如图,中,平分,且平分,于,于.
(1)说明的理由;
(2)如果,,求、的长.
【解】:(1)证明:连接,,
平分,,,
,,
且平分,
,
在与中,
,
,
;
(2)解:在和中,
,
,
,
设,则,
,,,,
,
解得:,
,.
22.如图,在平面直角坐标系中,已知过,,且、满足,将线段向右平移1个单位长度后,再向上平移2个单位长度,得到线段,其中点与点对应,点与点对应,连接,,.
(1)求点、、、的坐标.
(2)在坐标轴上是否存在点,使的面积等于四边形的面积?若存在,求点的坐标;若不存在,说明理由.
【解】:(1),满足,
,且,
,,
,,
由平移的性质得:,;
(2)解:存在,理由如下:
设,
由(1)得:,,
,
,
,
解得:,或,
点的坐标为或.
23.如图,在中,是边上一点,是的中点,过作的平行线交的延长线,且,连接.
(1)求证:点是的中点;
(2)如果,试判断四边形的形状,并证明你的结论;
(3)在(2)的条件下,当满足什么条件时,四边形为正方形,并说明理由.
【解】:(1)证明:,
,
点为的中点,
,
在和中,
,
,
,
,
,
是的中点;
(2)四边形为矩形;
证明:,,
四边形为平行四边形,
,,
,
,
四边形为矩形;
(3)若是等腰直角三角形时,四边形是正方形,理由如下:
,
,
,
;
,,
四边形是平行四边形,
,,
,,
平行四边形是正方形.
一.选择题(共10小题,每小题3分,共30分)
1.已知,如果以,的长为直角边作一个直角三角形,那么这个直角三角形的斜边长为
A. B.5 C. D.
2.如图, 直线,,表示三条公路 . 现要建造一个中转站,使到三条公路的距离都相等, 则中转站可选择的点有
A . 一处 B . 二处 C . 三处 D . 四处
3.下列关于平行四边形性质叙述正确的个数是
①平行四边形的对边平行,②平行四边形的对边相等,③平行四边形的对角相等,④平行四边形的对角线相等.
A.1 B.2 C.3 D.4
4.下列疫情防控标识图案中,是中心对称图形的是
A. B. C. D.
5.如图,,于,于,,交于,则以下结论:①;②;③点在的平分线上.正确的是
A.① B.② C.①② D.①②③
6.下列各点中,关于原点对称的两个点是
A.与 B.与
C.与 D.与
7.如图,平行四边形中,是上一点,、分别是、的平分线,若,,则平行四边形的面积为
A.96 B.48 C.60 D.30
8.小玲的爸爸在制作平行四边形框架时,采用了一种方法:如图所示,将两根木条,的中点重叠,并用钉子固定,则四边形就是平行四边形,这种方法的依据是
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对边分别平行的四边形是平行四边形
9.如图,是棋盘的一部分,建立适当的平面直角坐标系,已知棋子“车”的坐标为,棋子“炮”的坐标为,则棋子“马”的坐标为
A. B. C. D.
10.已知等腰中,于点,且,则底角的度数为
A. B. C. D.,或
二.填空题(共8小题,每小题3分,共24分)
11.如图,在中,,将折叠,使点落在边上的点处,折痕为;若,则 .
12.如图,直线、垂直相交于点,曲线关于点成中心对称,点的对称点是点,于点,于点.若,,则阴影部分的面积之和为 .
13.已知在中,,点、分别是、的中点,连接,在上有一点,,连接,,若,则 .
14.在平面直角坐标系中,若点在轴上,则的值是 .
15.平行四边形的对角线与相交于点,且,请添加一个条件: ,使得平行四边形为正方形.
16.已知平面直角坐标系内不同的两点和到轴的距离相等,则的值为 .
17.菱形的周长为,对角线和相交于点,,则菱形的面积为 .
18.如图,△中,,,.点,,分别是边,,的中点;点,,分别是边,,的中点;以此类推,则△的周长是 .
三.解答题(共5小题,满分46分,其中19题6分,20-24每小题8分)
19.如图,在四边形中,,是边上一点,,交于点.
(1)若,求的度数;
(2)若,平分,试说明:.
20.在中,、分别是,边上的点,且.
(1)求证:四边形是平行四边形;
(2)连接,若平分,,,,求的长.
21.如图,中,平分,且平分,于,于.
(1)说明的理由;
(2)如果,,求、的长.
22.如图,在平面直角坐标系中,已知过,,且、满足,将线段向右平移1个单位长度后,再向上平移2个单位长度,得到线段,其中点与点对应,点与点对应,连接,,.
(1)求点、、、的坐标.
(2)在坐标轴上是否存在点,使的面积等于四边形的面积?若存在,求点的坐标;若不存在,说明理由.
23.如图,在中,是边上一点,是的中点,过作的平行线交的延长线,且,连接.
(1)求证:点是的中点;
(2)如果,试判断四边形的形状,并证明你的结论;
(3)在(2)的条件下,当满足什么条件时,四边形为正方形,并说明理由.
湖南省澧县张公庙中学2021-2022学年湘教版八年级数学下册期中复习试卷(一)参考简答
一.选择题(共10小题)
1.. 2.. 3.. 4.. 5.. 6.. 7.. 8..
9.. 10..
二.填空题(共8小题)
11. 39 . 12. 12 . 13. . 14. .
15. 或 . 16. 1或 . 17. 4 .
18. .
三.解答题(共5小题)
19.如图,在四边形中,,是边上一点,,交于点.
(1)若,求的度数;
(2)若,平分,试说明:.
【解】:(1),
,
四边形的内角和是,
,,
;
(2)证明:四边形的内角和是,,,
,
,
,
平分,
,
,
,,,
.
20.在中,、分别是,边上的点,且.
(1)求证:四边形是平行四边形;
(2)连接,若平分,,,,求的长.
【解】:(1)证明:四边形是平行四边形,
,,,,
,
,
,
,
,
四边形是平行四边形;
(2)四边形是平行四边形,
,,
四边形是平行四边形,
,
,
平分,
,
,
,
在中,,,,
,
是直角三角形,
,
,
在中,.
21.如图,中,平分,且平分,于,于.
(1)说明的理由;
(2)如果,,求、的长.
【解】:(1)证明:连接,,
平分,,,
,,
且平分,
,
在与中,
,
,
;
(2)解:在和中,
,
,
,
设,则,
,,,,
,
解得:,
,.
22.如图,在平面直角坐标系中,已知过,,且、满足,将线段向右平移1个单位长度后,再向上平移2个单位长度,得到线段,其中点与点对应,点与点对应,连接,,.
(1)求点、、、的坐标.
(2)在坐标轴上是否存在点,使的面积等于四边形的面积?若存在,求点的坐标;若不存在,说明理由.
【解】:(1),满足,
,且,
,,
,,
由平移的性质得:,;
(2)解:存在,理由如下:
设,
由(1)得:,,
,
,
,
解得:,或,
点的坐标为或.
23.如图,在中,是边上一点,是的中点,过作的平行线交的延长线,且,连接.
(1)求证:点是的中点;
(2)如果,试判断四边形的形状,并证明你的结论;
(3)在(2)的条件下,当满足什么条件时,四边形为正方形,并说明理由.
【解】:(1)证明:,
,
点为的中点,
,
在和中,
,
,
,
,
,
是的中点;
(2)四边形为矩形;
证明:,,
四边形为平行四边形,
,,
,
,
四边形为矩形;
(3)若是等腰直角三角形时,四边形是正方形,理由如下:
,
,
,
;
,,
四边形是平行四边形,
,,
,,
平行四边形是正方形.
同课章节目录
