上海市青浦区2021-2022学年第二学期九年级数学期中线上练习试卷(PDF版无答案)
文档属性
| 名称 | 上海市青浦区2021-2022学年第二学期九年级数学期中线上练习试卷(PDF版无答案) |  | |
| 格式 | |||
| 文件大小 | 504.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-22 22:17:00 | ||
图片预览

文档简介
2021 学年第二学期 九年级数学期中线上练习
班级___________姓名____________
一、选择
1. 在 Rt△ABC 中,∠C=90°,∠A 的余弦是……………………………………………( )
AB BC AC AC
A. B. C. D.
AC AB AB BC
2. 已知非零向量 a和单位向量 e,那么下列结论中,正确的是…………………………( )
A. a = e a 1B. e = a C. a = e a D. a = a e
a
3. 下列二次根式的被开方数中,各因式指数为 1 的有……………………………………( )
2
A. 4x + 9y
2
B. 5x
2 y C. 12(x + y) 2 2D. x 2xy + y
4. 下列说法中,错误的有………………………………………………………………………( )
①2 能被 6 整除; ②把 16开平方得 16的平方根,表示为 16 = 4;
n
③把 237145 精确到万位是 240000; ④ a,规定am = m对于实数 an .
A. 1 个 B. 2 个 C. 3 个 D. 4 个
5. 下列关于代数式的说法中,正确的有…………………………………………………………( )
x2
①单项式 22022 系数是 2,次数是 2022 次; ②多项式 +1是一次二项; y
x
③ 29 是二次根式; ④对于实数a, a = a .
A. 1 个 B. 2 个 C. 3 个 D. 4 个
6. 如图,在平面直角坐标系中,已知 A(2,1), B (0,2),以 A 为顶点,BA 为 B
A
一边作 45°角,角的另一边交 y 轴于 C(C 在 B 上方),则 C 坐标为( ) O x
22 13
A. (0,6) B. (0,7) C. 0, D. 0,
3 2
二、填空
1
0 22
7. 如果从 、 、 1、93 、 tan 30 任意选取一个数,选到的数是无理数的概率为_______.
7
2
8. 将抛物线 C 向左平移 2 个单位,向上平移 1 个单位后,所得抛物线为 y = (x 1) ,则抛物线 C
解析式为______________.
2
9. 抛物线 y = (a 1) x 2x +3在对称轴左侧,y 随 x 的增大而增大,则a的取值范围是________.
10. 为防治新冠病毒,某医药公司一月份的产值为 1 亿元,若每月平均增
长率为 x,第一季度的总产值为 y(亿元),则 y 关于 x 的函数解析式
为___________________.
36°
11. 如图,是实验室里一批种子的发芽天数统计图,其中“1 天发芽”的圆
心角和“3 天发芽”的百分比如图所示,“2 天发芽”与“4 天发芽”的扇形 50%
弧长相等. 则这批种子的平均发芽天数为_________.
12. 已知正多边形每个内角的度数为 144°,则正多边形的边长与半径的比值为___________
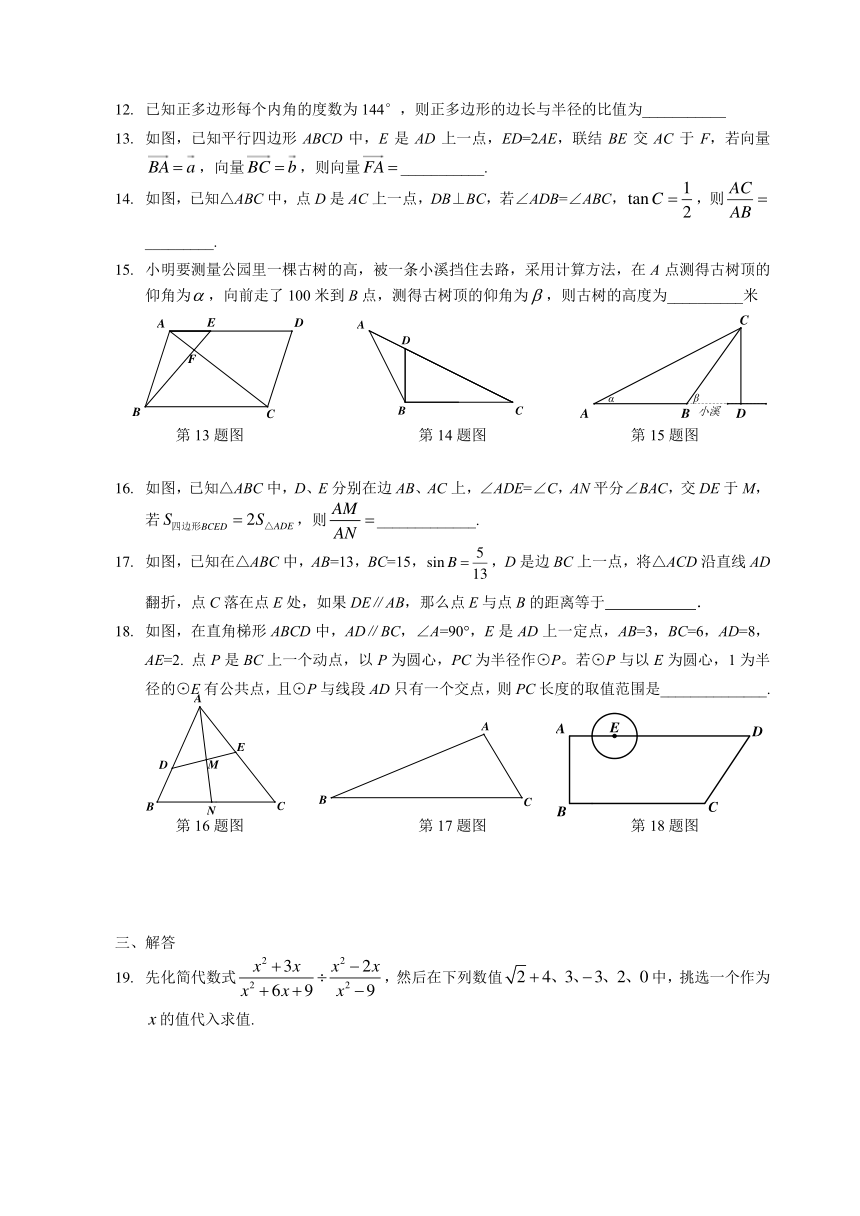
13. 如图,已知平行四边形 ABCD 中,E 是 AD 上一点,ED=2AE,联结 BE 交 AC 于 F,若向量
BA = a ,向量BC = b,则向量FA = ___________.
1 AC
14. 如图,已知△ABC 中,点 D 是 AC 上一点,DB⊥BC,若∠ADB=∠ABC,tan C = ,则 =
2 AB
_________.
15. 小明要测量公园里一棵古树的高,被一条小溪挡住去路,采用计算方法,在 A 点测得古树顶的
仰角为 ,向前走了 100 米到 B 点,测得古树顶的仰角为 ,则古树的高度为__________米
A
E D A C
D
F
α β
B C B C A B 小溪 D
第 13 题图 第 14 题图 第 15 题图
16. 如图,已知△ABC 中,D、E 分别在边 AB、AC 上,∠ADE=∠C,AN 平分∠BAC,交 DE 于 M,
AM
若 S = 2S四边形 △ADE ,则 = _____________. BCED
AN
5
17. 如图,已知在△ABC 中,AB=13,BC=15,sin B = ,D 是边 BC 上一点,将△ACD 沿直线 AD
13
翻折,点 C 落在点 E 处,如果 DE∥AB,那么点 E 与点 B 的距离等于 .
18. 如图,在直角梯形 ABCD 中,AD∥BC,∠A=90°,E 是 AD 上一定点,AB=3,BC=6,AD=8,
AE=2. 点 P 是 BC 上一个动点,以 P 为圆心,PC 为半径作⊙P。若⊙P 与以 E 为圆心,1 为半
径的⊙E 有公共点,且⊙P 与线段 AD 只有一个交点,则 PC 长度的取值范围是______________.
A
A A E D
E
D M
B
B C CN B C
第 16 题图 第 17 题图 第 18 题图
三、解答
x2 + 3x x2 2x
19. 先化简代数式 ,然后在下列数值 2 + 4、3、 3、2、0 中,挑选一个作为
x2 + 6x + 9 x2 9
x 的值代入求值.
2x 1 5x
20. 解不等式组: x x 1 并写出它的自然数解.
+ 2
5 3
21. (本题满分 10 分)
频率 图表2
为了解某区 3200 名学生放学后在校体育运动的情 组距 学生放学后体育运动时间
况,调研组选择了有 600 名学生的 W 校,抽取 40 名学生 0.04
进行调查,调查情况具体如下表 0.03
0.025
图表 1:感兴趣的运动项目 0.02
0.015
项目 乒乓球 篮球 足球 羽毛球 健美操 0.01
人数 4 16 10 4 6 0 10 20 30 40 50 t(分钟)
(1) 此次调查的总体是
________________________________________,样本容量是___________
(2) 若从 9 年级某学习加强班进行抽样调查,则这样的调查__________(“合适”,“不合适”),原
因是样本不是_________样本;
(3) 根据图表 1,估计该校对篮球感兴趣的学生的总人数为____________;
(4) 根据图表 2,若从左至右依次是第一、二、三、四、五组,则中位数落在第______组.
(5) 若要从对篮球感兴趣的同学中选拔出一支篮球队来,现在有以下两名学生的投篮数据,记录的
是每 10 次投篮命中的个数。
甲同学:10、5、7、9、4;乙同学:7、8、7、6、7.
若想要选择更稳定的同学,你会选择计算这两组数据的_________,因为这个量可以代表数据
的_____________. 请计算出你所填写的统计量,并且根据计算的结果,选择合适的队员。
22. 如图,已知 AB 是⊙O 的直径,P 是 AO 上一点,点 C、D 在直径两侧的圆周上,若 PB 平分∠
A
CPD,求证:劣弧 BC 与劣弧 BD 相等.
P
O
C
D
B
23. (本题满分 12 分,每小题满分 6 分)
如图,已知在梯形 ABCD 中,AD∥BC,对角线 AC、BD 交于 E,BD 平分∠ABC,点 G 在底边 BC
上,联结 DG 交对角线 AC 于 F,∠DGB=∠DAB. A D
E
(1) 求证:四边形 ABGD 是菱形.
F
(2) 联结 EG,求证:BG EG = BC EF .
B C G
24. (第(1)问 3 分,第(2)问 4 分,第(3)问 5 分)
已知直线 y = kx +b经过点 A( 2, 0),B (1, 3) 2两点,抛物线 y = ax 4ax+b与已知直线交于
C 、 D 两点(点C 在点 D 的右侧),顶点为P . y
(1)求直线 y = kx+b的表达式;
(2)若抛物线的顶点不在第一象限,求a的取值范围;
(3)若直线DP与直线 AB 所成夹角的余切值等于 3,求抛物
线 y = ax2 4ax+b的表达式.
o x
25. (第(1)问 4 分,第(2)问 5 分,第(3)问 5 分)
4
梯形 ABCD 中,AD∥BC,DC⊥BC 于点 C,AB = 10,tanB= ,⊙O1以 AB 为直径,⊙O2 以
3
CD 为直径,直线 O1O2与⊙O1 交于点 M,与⊙O2 交于点 N(如图 1),设 AD = x.
(1) 记两圆交点为 E、F(E 在上方),当 EF=6 时,求 x 的值;
(2) 当⊙O2与线段 AO1交于 P、Q 时,设 PQ=y,求 y 关于 x 的函数关系式,并写出定义域;
(3) 联结 AM,线段 AM 与⊙O2 交于点 G,分别联结 NG、O2G,若△GMN 与△GNO2相似,求 x 的
值. A D
E
O1
ON 2M
F
B C
AE D
P
Q
O1
N O2 M
B F C
A
O1
M
B
班级___________姓名____________
一、选择
1. 在 Rt△ABC 中,∠C=90°,∠A 的余弦是……………………………………………( )
AB BC AC AC
A. B. C. D.
AC AB AB BC
2. 已知非零向量 a和单位向量 e,那么下列结论中,正确的是…………………………( )
A. a = e a 1B. e = a C. a = e a D. a = a e
a
3. 下列二次根式的被开方数中,各因式指数为 1 的有……………………………………( )
2
A. 4x + 9y
2
B. 5x
2 y C. 12(x + y) 2 2D. x 2xy + y
4. 下列说法中,错误的有………………………………………………………………………( )
①2 能被 6 整除; ②把 16开平方得 16的平方根,表示为 16 = 4;
n
③把 237145 精确到万位是 240000; ④ a,规定am = m对于实数 an .
A. 1 个 B. 2 个 C. 3 个 D. 4 个
5. 下列关于代数式的说法中,正确的有…………………………………………………………( )
x2
①单项式 22022 系数是 2,次数是 2022 次; ②多项式 +1是一次二项; y
x
③ 29 是二次根式; ④对于实数a, a = a .
A. 1 个 B. 2 个 C. 3 个 D. 4 个
6. 如图,在平面直角坐标系中,已知 A(2,1), B (0,2),以 A 为顶点,BA 为 B
A
一边作 45°角,角的另一边交 y 轴于 C(C 在 B 上方),则 C 坐标为( ) O x
22 13
A. (0,6) B. (0,7) C. 0, D. 0,
3 2
二、填空
1
0 22
7. 如果从 、 、 1、93 、 tan 30 任意选取一个数,选到的数是无理数的概率为_______.
7
2
8. 将抛物线 C 向左平移 2 个单位,向上平移 1 个单位后,所得抛物线为 y = (x 1) ,则抛物线 C
解析式为______________.
2
9. 抛物线 y = (a 1) x 2x +3在对称轴左侧,y 随 x 的增大而增大,则a的取值范围是________.
10. 为防治新冠病毒,某医药公司一月份的产值为 1 亿元,若每月平均增
长率为 x,第一季度的总产值为 y(亿元),则 y 关于 x 的函数解析式
为___________________.
36°
11. 如图,是实验室里一批种子的发芽天数统计图,其中“1 天发芽”的圆
心角和“3 天发芽”的百分比如图所示,“2 天发芽”与“4 天发芽”的扇形 50%
弧长相等. 则这批种子的平均发芽天数为_________.
12. 已知正多边形每个内角的度数为 144°,则正多边形的边长与半径的比值为___________
13. 如图,已知平行四边形 ABCD 中,E 是 AD 上一点,ED=2AE,联结 BE 交 AC 于 F,若向量
BA = a ,向量BC = b,则向量FA = ___________.
1 AC
14. 如图,已知△ABC 中,点 D 是 AC 上一点,DB⊥BC,若∠ADB=∠ABC,tan C = ,则 =
2 AB
_________.
15. 小明要测量公园里一棵古树的高,被一条小溪挡住去路,采用计算方法,在 A 点测得古树顶的
仰角为 ,向前走了 100 米到 B 点,测得古树顶的仰角为 ,则古树的高度为__________米
A
E D A C
D
F
α β
B C B C A B 小溪 D
第 13 题图 第 14 题图 第 15 题图
16. 如图,已知△ABC 中,D、E 分别在边 AB、AC 上,∠ADE=∠C,AN 平分∠BAC,交 DE 于 M,
AM
若 S = 2S四边形 △ADE ,则 = _____________. BCED
AN
5
17. 如图,已知在△ABC 中,AB=13,BC=15,sin B = ,D 是边 BC 上一点,将△ACD 沿直线 AD
13
翻折,点 C 落在点 E 处,如果 DE∥AB,那么点 E 与点 B 的距离等于 .
18. 如图,在直角梯形 ABCD 中,AD∥BC,∠A=90°,E 是 AD 上一定点,AB=3,BC=6,AD=8,
AE=2. 点 P 是 BC 上一个动点,以 P 为圆心,PC 为半径作⊙P。若⊙P 与以 E 为圆心,1 为半
径的⊙E 有公共点,且⊙P 与线段 AD 只有一个交点,则 PC 长度的取值范围是______________.
A
A A E D
E
D M
B
B C CN B C
第 16 题图 第 17 题图 第 18 题图
三、解答
x2 + 3x x2 2x
19. 先化简代数式 ,然后在下列数值 2 + 4、3、 3、2、0 中,挑选一个作为
x2 + 6x + 9 x2 9
x 的值代入求值.
2x 1 5x
20. 解不等式组: x x 1 并写出它的自然数解.
+ 2
5 3
21. (本题满分 10 分)
频率 图表2
为了解某区 3200 名学生放学后在校体育运动的情 组距 学生放学后体育运动时间
况,调研组选择了有 600 名学生的 W 校,抽取 40 名学生 0.04
进行调查,调查情况具体如下表 0.03
0.025
图表 1:感兴趣的运动项目 0.02
0.015
项目 乒乓球 篮球 足球 羽毛球 健美操 0.01
人数 4 16 10 4 6 0 10 20 30 40 50 t(分钟)
(1) 此次调查的总体是
________________________________________,样本容量是___________
(2) 若从 9 年级某学习加强班进行抽样调查,则这样的调查__________(“合适”,“不合适”),原
因是样本不是_________样本;
(3) 根据图表 1,估计该校对篮球感兴趣的学生的总人数为____________;
(4) 根据图表 2,若从左至右依次是第一、二、三、四、五组,则中位数落在第______组.
(5) 若要从对篮球感兴趣的同学中选拔出一支篮球队来,现在有以下两名学生的投篮数据,记录的
是每 10 次投篮命中的个数。
甲同学:10、5、7、9、4;乙同学:7、8、7、6、7.
若想要选择更稳定的同学,你会选择计算这两组数据的_________,因为这个量可以代表数据
的_____________. 请计算出你所填写的统计量,并且根据计算的结果,选择合适的队员。
22. 如图,已知 AB 是⊙O 的直径,P 是 AO 上一点,点 C、D 在直径两侧的圆周上,若 PB 平分∠
A
CPD,求证:劣弧 BC 与劣弧 BD 相等.
P
O
C
D
B
23. (本题满分 12 分,每小题满分 6 分)
如图,已知在梯形 ABCD 中,AD∥BC,对角线 AC、BD 交于 E,BD 平分∠ABC,点 G 在底边 BC
上,联结 DG 交对角线 AC 于 F,∠DGB=∠DAB. A D
E
(1) 求证:四边形 ABGD 是菱形.
F
(2) 联结 EG,求证:BG EG = BC EF .
B C G
24. (第(1)问 3 分,第(2)问 4 分,第(3)问 5 分)
已知直线 y = kx +b经过点 A( 2, 0),B (1, 3) 2两点,抛物线 y = ax 4ax+b与已知直线交于
C 、 D 两点(点C 在点 D 的右侧),顶点为P . y
(1)求直线 y = kx+b的表达式;
(2)若抛物线的顶点不在第一象限,求a的取值范围;
(3)若直线DP与直线 AB 所成夹角的余切值等于 3,求抛物
线 y = ax2 4ax+b的表达式.
o x
25. (第(1)问 4 分,第(2)问 5 分,第(3)问 5 分)
4
梯形 ABCD 中,AD∥BC,DC⊥BC 于点 C,AB = 10,tanB= ,⊙O1以 AB 为直径,⊙O2 以
3
CD 为直径,直线 O1O2与⊙O1 交于点 M,与⊙O2 交于点 N(如图 1),设 AD = x.
(1) 记两圆交点为 E、F(E 在上方),当 EF=6 时,求 x 的值;
(2) 当⊙O2与线段 AO1交于 P、Q 时,设 PQ=y,求 y 关于 x 的函数关系式,并写出定义域;
(3) 联结 AM,线段 AM 与⊙O2 交于点 G,分别联结 NG、O2G,若△GMN 与△GNO2相似,求 x 的
值. A D
E
O1
ON 2M
F
B C
AE D
P
Q
O1
N O2 M
B F C
A
O1
M
B
同课章节目录
