物理人教版(2019)必修第二册6.4生活中的圆周运动(共17张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第二册6.4生活中的圆周运动(共17张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-22 10:20:29 | ||
图片预览





文档简介
(共17张PPT)
6.4 生活中的圆周运动
1.变速圆周运动:
轨迹为圆,速度大小发生改变
2. 加速度:可以分解为向心加速度(法向)、切向加速度
a切:改变v大小
a法:改变速度方向
三、 变速圆周运动
2. 合外力:可分解为法向合外力、切向合外力
F切改变速度的大小
F法=改变速度的方向
三、 变速圆周运动
F法
F切
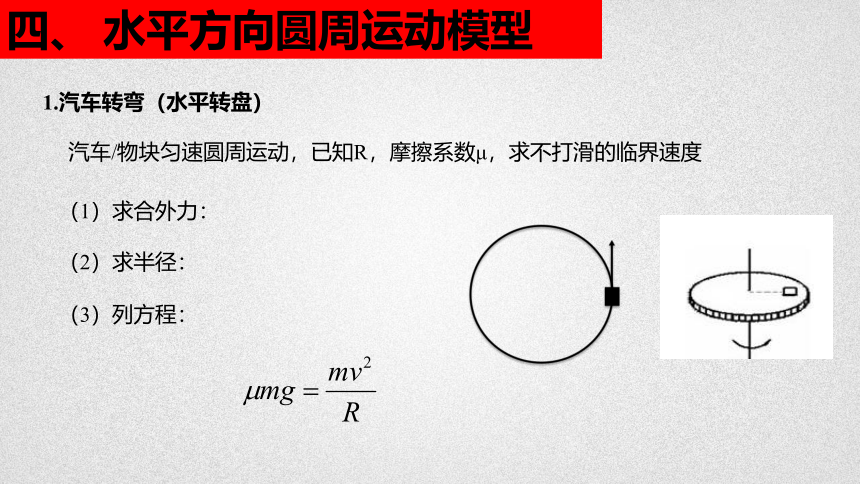
四、 水平方向圆周运动模型
1.汽车转弯(水平转盘)
汽车/物块匀速圆周运动,已知R,摩擦系数μ,求不打滑的临界速度
(1)求合外力:
(2)求半径:
(3)列方程:
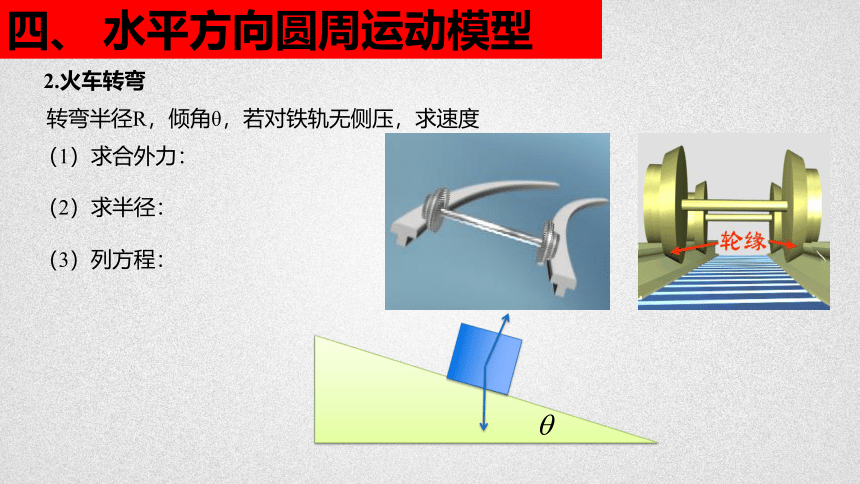
2.火车转弯
(1)求合外力:
(2)求半径:
(3)列方程:
转弯半径R,倾角θ,若对铁轨无侧压,求速度
四、 水平方向圆周运动模型
汽车跑道做成斜坡的目的是什么?
已知R,摩擦系数μ,拐弯斜面与地面夹角θ,求拐弯安全速度
某赛车场地为圆形,半径为100m。一赛车和乘客的总质量为100kg,车轮胎与地面间的最大静摩擦力为600N。
(1)若赛车的速度达到72km/h,运动员操作正确,这辆车在运动过程中有没有可能发生滑出赛道的事故?(通过计算说明)
(2)若将场地建成外高内低的圆形赛道,且倾角为37°,并假设车轮和地面之间的最大静摩擦力大小不变,为保证赛车的行驶安全,赛车行驶的最大速度应为多大?(取g=10m/s2,sin37 =0.6,cos37 =0.8)
四、 竖直方向圆周运动模型
(1)均为变速圆周运动
绳
杆
单侧轨
(2)绳子和单侧轨提供的力向心
1.竖直方向圆周运动模型
拱桥
(3)拱桥在最低/高点提供的力向上
绳球模型
A
B
(1)A点:
2. 绳球模型
(2)B点:
四、 竖直方向圆周运动模型
杆球模型
3. 杆球模型
(1)A点:
F
(2)B点:
假设F向下
①
②
向下
③
向上
F向上
A
B
四、 竖直方向圆周运动模型
一轻杆一端固定质量为m 的小球,以另一端O 为圆心,使小球在竖直平面内作半径为R 的圆周运动,如图所示,则( )
A.小球过最高点时,杆所受弹力可以为零
B.小球过最高点时的最小速度是gR
C.小球过最高点时杆对球的作用力可以竖直向上,但此时重力一定大于杆对球的作用力
D.小球过最高点时,杆对球的作用力一定跟小球所受重力的方向相反
单侧轨模型
4. 单侧轨模型
时,最高点FN=0
(3)最
四、 竖直方向圆周运动模型
A
B
质量为m 的小球在竖直平面内的圆形轨道的内侧运动,经过最高点而不脱离轨道的最小速度是v,则当小球以2v 的速度经过最高点时,对轨道压力的大小是( )
A.0 B.mg C.3mg D.5mg
5.拱桥模型
汽车质量m,速度v,桥面的圆弧半径R,分析汽车通过桥的最高点时对桥的压力.求过桥安全速度(不腾空飞起)
mg
FN
a
四、 竖直圆周运动模型
(1)求合外力:
(2)求半径:
(3)列方程:
mg
FN
a
汽车质量为m的,速度为v,桥面的圆弧半径为R,分析汽车通过桥的最低点时对桥的压力
(1)求合外力:
(2)求半径:
(3)列方程:
F压=FN <mg
失重
超重
F压=FN =mg
F压=FN >mg
2. 如图所示,当汽车通过拱桥顶点的速度为 10 米/秒时,车对桥顶的压力为车重的 3/4,如果要使汽车在粗糙的桥面行驶至桥顶时,不受摩擦力作用,则汽车通过桥顶的速度应为(g=10m/s2)( )
A.15m/s B.20m/s
C.25m/s D.30m/s
1. 如图 所示,质量一定的汽车驶过圆弧形桥面顶点时未脱离桥面,关于汽车所处的运动状态以及对桥面的压力,以下说法正确的是( )
A.汽车处于超重状态,它对桥面的压力大于汽车的重力
B.汽车处于超重状态,它对桥面的压力小于汽车的重力
C.汽车处于失重状态,它对桥面的压力大于汽车的重力
D.汽车处于失重状态,它对桥面的压力小于汽车的重力
6.4 生活中的圆周运动
1.变速圆周运动:
轨迹为圆,速度大小发生改变
2. 加速度:可以分解为向心加速度(法向)、切向加速度
a切:改变v大小
a法:改变速度方向
三、 变速圆周运动
2. 合外力:可分解为法向合外力、切向合外力
F切改变速度的大小
F法=改变速度的方向
三、 变速圆周运动
F法
F切
四、 水平方向圆周运动模型
1.汽车转弯(水平转盘)
汽车/物块匀速圆周运动,已知R,摩擦系数μ,求不打滑的临界速度
(1)求合外力:
(2)求半径:
(3)列方程:
2.火车转弯
(1)求合外力:
(2)求半径:
(3)列方程:
转弯半径R,倾角θ,若对铁轨无侧压,求速度
四、 水平方向圆周运动模型
汽车跑道做成斜坡的目的是什么?
已知R,摩擦系数μ,拐弯斜面与地面夹角θ,求拐弯安全速度
某赛车场地为圆形,半径为100m。一赛车和乘客的总质量为100kg,车轮胎与地面间的最大静摩擦力为600N。
(1)若赛车的速度达到72km/h,运动员操作正确,这辆车在运动过程中有没有可能发生滑出赛道的事故?(通过计算说明)
(2)若将场地建成外高内低的圆形赛道,且倾角为37°,并假设车轮和地面之间的最大静摩擦力大小不变,为保证赛车的行驶安全,赛车行驶的最大速度应为多大?(取g=10m/s2,sin37 =0.6,cos37 =0.8)
四、 竖直方向圆周运动模型
(1)均为变速圆周运动
绳
杆
单侧轨
(2)绳子和单侧轨提供的力向心
1.竖直方向圆周运动模型
拱桥
(3)拱桥在最低/高点提供的力向上
绳球模型
A
B
(1)A点:
2. 绳球模型
(2)B点:
四、 竖直方向圆周运动模型
杆球模型
3. 杆球模型
(1)A点:
F
(2)B点:
假设F向下
①
②
向下
③
向上
F向上
A
B
四、 竖直方向圆周运动模型
一轻杆一端固定质量为m 的小球,以另一端O 为圆心,使小球在竖直平面内作半径为R 的圆周运动,如图所示,则( )
A.小球过最高点时,杆所受弹力可以为零
B.小球过最高点时的最小速度是gR
C.小球过最高点时杆对球的作用力可以竖直向上,但此时重力一定大于杆对球的作用力
D.小球过最高点时,杆对球的作用力一定跟小球所受重力的方向相反
单侧轨模型
4. 单侧轨模型
时,最高点FN=0
(3)最
四、 竖直方向圆周运动模型
A
B
质量为m 的小球在竖直平面内的圆形轨道的内侧运动,经过最高点而不脱离轨道的最小速度是v,则当小球以2v 的速度经过最高点时,对轨道压力的大小是( )
A.0 B.mg C.3mg D.5mg
5.拱桥模型
汽车质量m,速度v,桥面的圆弧半径R,分析汽车通过桥的最高点时对桥的压力.求过桥安全速度(不腾空飞起)
mg
FN
a
四、 竖直圆周运动模型
(1)求合外力:
(2)求半径:
(3)列方程:
mg
FN
a
汽车质量为m的,速度为v,桥面的圆弧半径为R,分析汽车通过桥的最低点时对桥的压力
(1)求合外力:
(2)求半径:
(3)列方程:
F压=FN <mg
失重
超重
F压=FN =mg
F压=FN >mg
2. 如图所示,当汽车通过拱桥顶点的速度为 10 米/秒时,车对桥顶的压力为车重的 3/4,如果要使汽车在粗糙的桥面行驶至桥顶时,不受摩擦力作用,则汽车通过桥顶的速度应为(g=10m/s2)( )
A.15m/s B.20m/s
C.25m/s D.30m/s
1. 如图 所示,质量一定的汽车驶过圆弧形桥面顶点时未脱离桥面,关于汽车所处的运动状态以及对桥面的压力,以下说法正确的是( )
A.汽车处于超重状态,它对桥面的压力大于汽车的重力
B.汽车处于超重状态,它对桥面的压力小于汽车的重力
C.汽车处于失重状态,它对桥面的压力大于汽车的重力
D.汽车处于失重状态,它对桥面的压力小于汽车的重力
