6.1圆周运动(共28张ppt)
文档属性
| 名称 | 6.1圆周运动(共28张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-22 13:29:51 | ||
图片预览








文档简介
(共28张PPT)
圆周运动
r
A
B
C
线速度v
线速度定义
物体通过的弧长,与所用时间的比值。单位:米/秒 (m/s)
r
A
B
C
t 时刻的瞬时速度
1、单位:m/s
2、矢量
足够小
线速度v
速度方向沿切线方向
若 s 等于圆的周长
(v 为线速度)
(周期)
周期定义:
做匀速圆周运动的物体,转过完整一圈
所用的时间,叫做周期,符号为T。
单位: 秒(s)
A
B
C
周期与线速度
转换关系
周期T
1、
1秒钟转10圈
1秒钟转0.5圈
转速定义
单位时间所转过的圈数,用n表示
单位:转/秒 (r/s)
或转/分钟 (r/min)
2、
频率定义
单位时间所完成的周期数,用f 表示
单位:赫兹 (Hz)
若 n 单位取转/秒(r/s)
转速=频率
转速n与频率f
转速:n=10 r/s
频率:f=10 Hz
转速:n=0.5 r/s
频率:f=0.5 Hz
周期与频率
转换关系
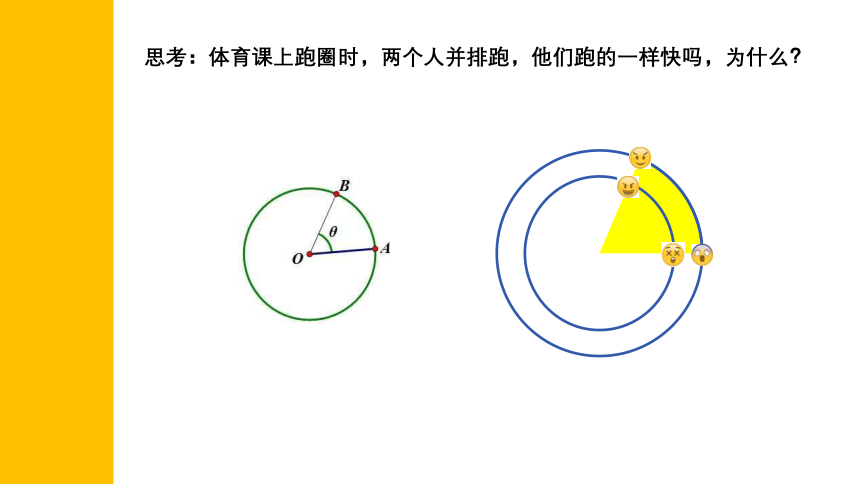
思考:体育课上跑圈时,两个人并排跑,他们跑的一样快吗,为什么?
角速度
角速度定义:
在圆周运动中,连接运动物体和圆心的半径,转过的弧度与所用的时间的比值,符号,单位rad/s
公式:
A
B
C
弧度
弧度定义:
弧长等于半径的一段弧,它所对应的圆心角为1弧度,单位rad
A
B
A
B
A
B
A(B)
弧度
角速度与线速度v、周期T
角速度与线速度
转换关系
角速度与周期
转换关系
角速度与频率
转换关系
三种算法求 线速度
A
B
已知
1、从A到B所用时间:2秒钟
2、半径:r=3m
求:线速度大小?
常见传动装置
1、同轴共线模型
A
C
B
线速度关系
1、同轴的两个圆,角速度相等
2、同传送带的两个圆,线速度相等
角速度关系
常见传动装置
2、齿轮模型
线速度关系
相互啮合的两个齿轮,线速度相等
角速度关系
向心
加速度
S
N
引力/
加速度
速度
引力/
加速度
速度
引力/
加速度
速度
引力/
加速度
速度
如果引力朝上,则速度向上偏
S
N
引力/
加速度
速度
引力/
加速度
速度
引力/
加速度
速度
引力/
加速度
速度
如果引力朝下,则速度向下偏
引力/
加速度
速度
引力/
加速度
速度
引力/
加速度
速度
引力/
加速度
速度
a
v
a
v
a
v
a
v
a
v
a
v
a
v
a
v
1、定义:
4、作用效果:
2、符号:
3、方向:
一、向心力:
做匀速圆周运动的物体始终受到一个_______________,这个力称为向心力。
Fn
始终指向圆心,方向不断发生改变。
只改变速度的方向,不改变速度的大小。
指向圆心的合外力
如果引力在不断变化,则物体做
圆周运动,向心加速度指向圆心,
速度沿着切线
向心加速度a
定义
做匀速圆周运动的物体,其加速度指向圆心,这个加速度称为
向心加速度。
方向
方向时刻在变化,总是沿着半径指向圆心,即始终与线速度垂直。
效果
只改变线速度的方向,不改变线速度的大小。
公式
向心加速度a
公式推导
对向心加速度的理解
1、无论向心加速度a大小是否变化,a的方向是时刻改变的,所以圆周运动一定是变加速曲线运动
2、加速度分解
2)向心加速度
作用:改变速度方向
3)切向加速度
作用:改变速度大小
1)a合加速度
作用:改变速度大小和方向
1.
2.
4. 如图所示的皮带传动装置,主动轮O1上两轮的半径分别为3r和r,从动轮O2的半径为2r,A、B、C分别为轮缘上的三点,设皮带不打滑,则A、B、C三点的角速度大小之比ωA:ωB:ωC=______,三点的线速度大小之比vA:vB:vC=______
3. 绳的一端拴着一个小球(将球视为质点),使其在水平面上做匀速圆周运动,3 s内转过的圆心角是120°,通过的弧长为6m,则球的角速度是________,线速度是________,周期是________,频率是________,转速是________;若细绳突然断了,则球的运动方向是_____________________。
5.(不定项)
a、b和c是玩具陀螺上的三个点,当陀螺绕垂直于地面的轴线以角速度ω稳定旋转时,下列表述正确的是( )
A. a、b和c三点的线速度大小相等
B. a、b和c三点的角速度相等
C. a、b的角速度比c的大
D. c的线速度比a、b的大
圆周运动
r
A
B
C
线速度v
线速度定义
物体通过的弧长,与所用时间的比值。单位:米/秒 (m/s)
r
A
B
C
t 时刻的瞬时速度
1、单位:m/s
2、矢量
足够小
线速度v
速度方向沿切线方向
若 s 等于圆的周长
(v 为线速度)
(周期)
周期定义:
做匀速圆周运动的物体,转过完整一圈
所用的时间,叫做周期,符号为T。
单位: 秒(s)
A
B
C
周期与线速度
转换关系
周期T
1、
1秒钟转10圈
1秒钟转0.5圈
转速定义
单位时间所转过的圈数,用n表示
单位:转/秒 (r/s)
或转/分钟 (r/min)
2、
频率定义
单位时间所完成的周期数,用f 表示
单位:赫兹 (Hz)
若 n 单位取转/秒(r/s)
转速=频率
转速n与频率f
转速:n=10 r/s
频率:f=10 Hz
转速:n=0.5 r/s
频率:f=0.5 Hz
周期与频率
转换关系
思考:体育课上跑圈时,两个人并排跑,他们跑的一样快吗,为什么?
角速度
角速度定义:
在圆周运动中,连接运动物体和圆心的半径,转过的弧度与所用的时间的比值,符号,单位rad/s
公式:
A
B
C
弧度
弧度定义:
弧长等于半径的一段弧,它所对应的圆心角为1弧度,单位rad
A
B
A
B
A
B
A(B)
弧度
角速度与线速度v、周期T
角速度与线速度
转换关系
角速度与周期
转换关系
角速度与频率
转换关系
三种算法求 线速度
A
B
已知
1、从A到B所用时间:2秒钟
2、半径:r=3m
求:线速度大小?
常见传动装置
1、同轴共线模型
A
C
B
线速度关系
1、同轴的两个圆,角速度相等
2、同传送带的两个圆,线速度相等
角速度关系
常见传动装置
2、齿轮模型
线速度关系
相互啮合的两个齿轮,线速度相等
角速度关系
向心
加速度
S
N
引力/
加速度
速度
引力/
加速度
速度
引力/
加速度
速度
引力/
加速度
速度
如果引力朝上,则速度向上偏
S
N
引力/
加速度
速度
引力/
加速度
速度
引力/
加速度
速度
引力/
加速度
速度
如果引力朝下,则速度向下偏
引力/
加速度
速度
引力/
加速度
速度
引力/
加速度
速度
引力/
加速度
速度
a
v
a
v
a
v
a
v
a
v
a
v
a
v
a
v
1、定义:
4、作用效果:
2、符号:
3、方向:
一、向心力:
做匀速圆周运动的物体始终受到一个_______________,这个力称为向心力。
Fn
始终指向圆心,方向不断发生改变。
只改变速度的方向,不改变速度的大小。
指向圆心的合外力
如果引力在不断变化,则物体做
圆周运动,向心加速度指向圆心,
速度沿着切线
向心加速度a
定义
做匀速圆周运动的物体,其加速度指向圆心,这个加速度称为
向心加速度。
方向
方向时刻在变化,总是沿着半径指向圆心,即始终与线速度垂直。
效果
只改变线速度的方向,不改变线速度的大小。
公式
向心加速度a
公式推导
对向心加速度的理解
1、无论向心加速度a大小是否变化,a的方向是时刻改变的,所以圆周运动一定是变加速曲线运动
2、加速度分解
2)向心加速度
作用:改变速度方向
3)切向加速度
作用:改变速度大小
1)a合加速度
作用:改变速度大小和方向
1.
2.
4. 如图所示的皮带传动装置,主动轮O1上两轮的半径分别为3r和r,从动轮O2的半径为2r,A、B、C分别为轮缘上的三点,设皮带不打滑,则A、B、C三点的角速度大小之比ωA:ωB:ωC=______,三点的线速度大小之比vA:vB:vC=______
3. 绳的一端拴着一个小球(将球视为质点),使其在水平面上做匀速圆周运动,3 s内转过的圆心角是120°,通过的弧长为6m,则球的角速度是________,线速度是________,周期是________,频率是________,转速是________;若细绳突然断了,则球的运动方向是_____________________。
5.(不定项)
a、b和c是玩具陀螺上的三个点,当陀螺绕垂直于地面的轴线以角速度ω稳定旋转时,下列表述正确的是( )
A. a、b和c三点的线速度大小相等
B. a、b和c三点的角速度相等
C. a、b的角速度比c的大
D. c的线速度比a、b的大
