青岛版九年级数学下册 7.2 直棱柱的侧面展开图(第2课时)课件(共18张PPT)
文档属性
| 名称 | 青岛版九年级数学下册 7.2 直棱柱的侧面展开图(第2课时)课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-24 07:33:40 | ||
图片预览



文档简介
(共21张PPT)
学习目标
多面体
直棱柱
斜棱柱
棱柱
新课导入
引例
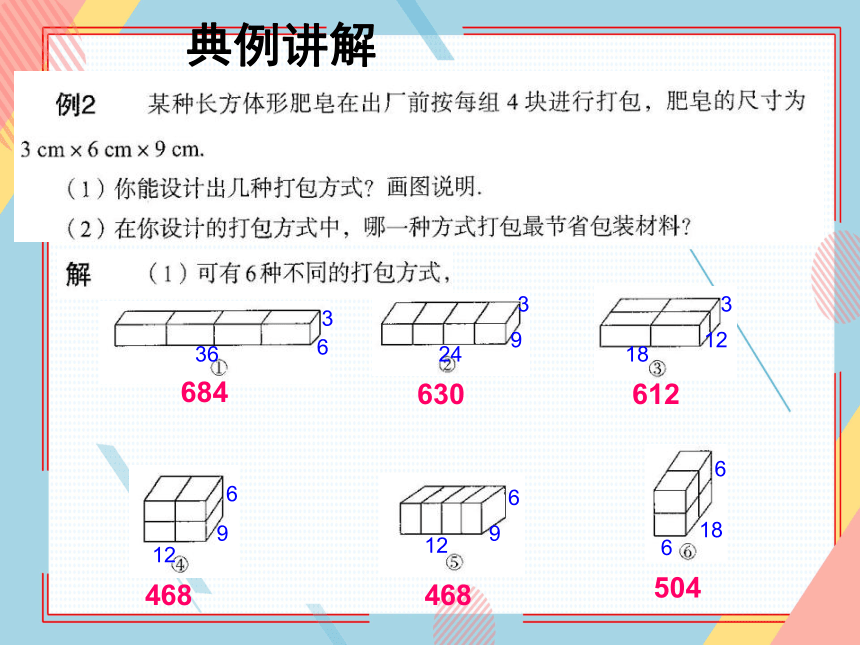
684
630
612
468
468
504
36
6
3
3
9
24
18
12
3
12
6
9
12
9
6
6
18
6
典例讲解
(1)
(2)
例3
D′
D
E
D′
C′
E
D′
C′
D′
A′
跟踪训练
B
6
3
随堂练习
B
6
B
3
B
3
6
2.
C
A
E
C
B
20
10
5
15
3.
本课小结
7.2直棱柱的侧面展开图
第2课时
米
米
学习目标
1.画出立体图形和对应的平面展开图制作实体模型
归纳出所在直角三角形的两直角边的一般性规律;
2.利用直棱柱的侧面展开图知识,解决几何体中最短
路径问题.
①
②
③
图7-5
例1
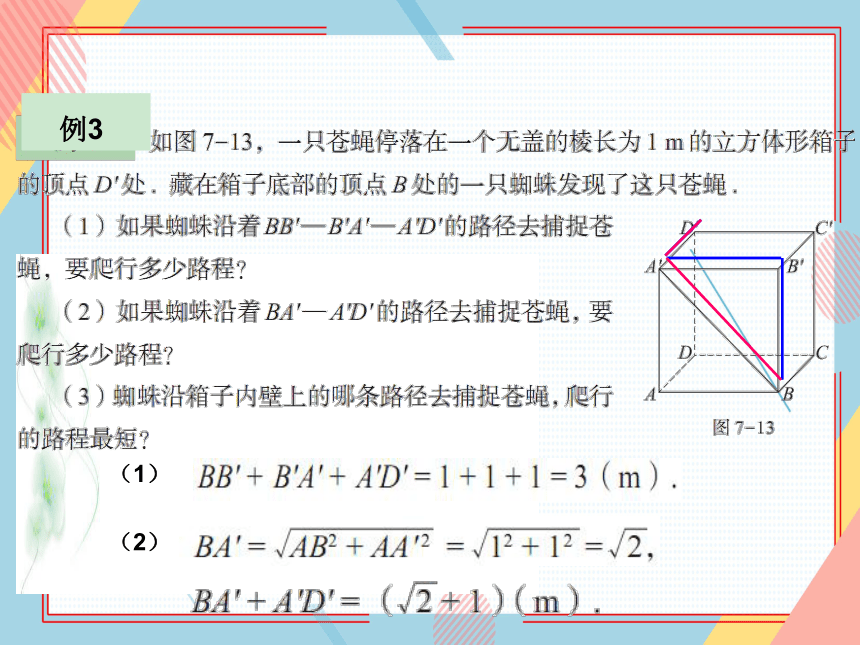
如图7-13,一只苍蝇停落在一个无盖的棱长为1m的立方体形箱子
的顶点D'处.藏在箱子底部的顶点B处的一只蜘蛛发现了这只苍蝇.
(1)如果蜘蛛沿着BB'一BA'一AD'的路径去捕捉苍
蝇,要爬行多少路程?
B'
(2)如果蜘蛛沿着BA'一AD'的路径去捕捉苍蝇,要
爬行多少路程?
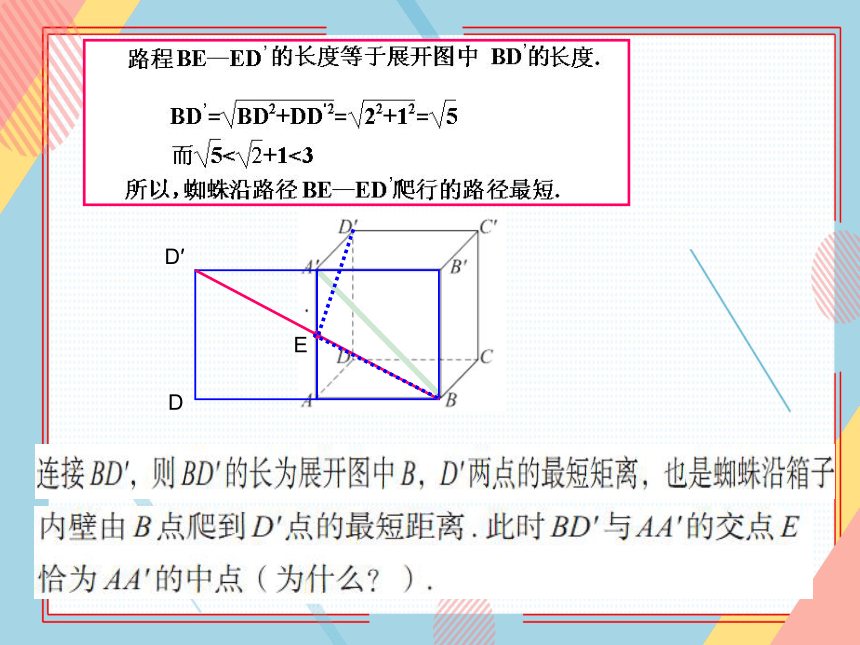
(3)蜘蛛沿箱子内壁上的哪条路径去捕捉苍蝇,爬行
的路程最短?
图7-13
跟踪训练
如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方
体的外表面爬到顶点B的最短距离是(B)
(A)3
(B)V5
(C)2
(D)1
B
C
2
B
1
A
分析:由于蚂蚁是沿正方体的外表面爬行的,故需把正方体
展开成平面图形(如图).
随堂练习
1.如图,是一块长,宽,高分别是6cm,4cm和3cm的长方
体木块一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体
的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬
行的最短路径的长是多少?
B
3
6
4
如图是一个三级台阶,它的每一级的长宽和高分别为20dm、
3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只
蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最
短路程是多少?
20
C
20
3
2
3
2
B
3
AB=25
2
本课小结
找方法、巧归纳
分别画出立体图形和对应的平面展开图制作实体模型
归纳出所在直角三角形的两直角边的一般性规律,并
记录在平面图或模型上.
利用直棱柱的侧面展开图,解决几何体最短路径问题
学习目标
多面体
直棱柱
斜棱柱
棱柱
新课导入
引例
684
630
612
468
468
504
36
6
3
3
9
24
18
12
3
12
6
9
12
9
6
6
18
6
典例讲解
(1)
(2)
例3
D′
D
E
D′
C′
E
D′
C′
D′
A′
跟踪训练
B
6
3
随堂练习
B
6
B
3
B
3
6
2.
C
A
E
C
B
20
10
5
15
3.
本课小结
7.2直棱柱的侧面展开图
第2课时
米
米
学习目标
1.画出立体图形和对应的平面展开图制作实体模型
归纳出所在直角三角形的两直角边的一般性规律;
2.利用直棱柱的侧面展开图知识,解决几何体中最短
路径问题.
①
②
③
图7-5
例1
如图7-13,一只苍蝇停落在一个无盖的棱长为1m的立方体形箱子
的顶点D'处.藏在箱子底部的顶点B处的一只蜘蛛发现了这只苍蝇.
(1)如果蜘蛛沿着BB'一BA'一AD'的路径去捕捉苍
蝇,要爬行多少路程?
B'
(2)如果蜘蛛沿着BA'一AD'的路径去捕捉苍蝇,要
爬行多少路程?
(3)蜘蛛沿箱子内壁上的哪条路径去捕捉苍蝇,爬行
的路程最短?
图7-13
跟踪训练
如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方
体的外表面爬到顶点B的最短距离是(B)
(A)3
(B)V5
(C)2
(D)1
B
C
2
B
1
A
分析:由于蚂蚁是沿正方体的外表面爬行的,故需把正方体
展开成平面图形(如图).
随堂练习
1.如图,是一块长,宽,高分别是6cm,4cm和3cm的长方
体木块一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体
的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬
行的最短路径的长是多少?
B
3
6
4
如图是一个三级台阶,它的每一级的长宽和高分别为20dm、
3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只
蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最
短路程是多少?
20
C
20
3
2
3
2
B
3
AB=25
2
本课小结
找方法、巧归纳
分别画出立体图形和对应的平面展开图制作实体模型
归纳出所在直角三角形的两直角边的一般性规律,并
记录在平面图或模型上.
利用直棱柱的侧面展开图,解决几何体最短路径问题
