数学北师大版(2019)必修第二册 6.1.3简单旋转体——球、圆柱、圆锥和圆台 课件(共23张PPT)
文档属性
| 名称 | 数学北师大版(2019)必修第二册 6.1.3简单旋转体——球、圆柱、圆锥和圆台 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 997.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-24 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
6.1.3 简单旋转体——球、圆柱、圆锥和圆台
课标阐释
1.了解球、圆柱、圆锥、圆台的定义.(数学抽象)
2.掌握球、圆柱、圆锥、圆台的结构特征,并能在几何体中进行相关的计算.(几何直观、数学运算)
3.了解简单组合体的概念及结构特征.(几何直观)
思维脉络
激趣诱思
知识点拨
素描是艺术类考生必须掌握的基本功之一,素描如果按表现内容可分为静物、动物、风景、人像等,其中几何体的素描就属于静物素描的范畴.要画好素描静物,必须打好石膏几何体这个基础,其中空间想象能力是必不可少的.下图是一位考生的素描作品,它是组合体,你能从中找出两个旋转体吗 是怎样旋转而成的 这两个旋转体互相交叉的部分形状如何
激趣诱思
知识点拨
一、球
1.球的定义、相关概念、图形及表示
球及相关概念 图形及表示
定义 以半圆的直径所在的直线为旋转轴,将半圆旋转一周所形成的曲面称为球面,球面所围成的几何体称为球体,简称球 用表示球心的字母表示
图中的球记作:球O
相关 概念 球心:半圆的圆心称为球心 半径:连接球心和球面上任意一点的线段称为球的半径 直径:连接球面上两点并且过球心的线段称为球的直径
激趣诱思
知识点拨
2.球的相关性质
(1)球面上所有的点到球心的距离都等于球的半径.
(2)用任何一个平面去截球面,得到的截面都是圆,其中过球心的平面截球面得到的半径最大,等于球的半径.
微拓展
(1)球的大圆:球面被经过球心的平面截得的圆.
(2)球的小圆:球面被不经过球心的平面截得的圆.
(3)两点的球面距离:在球面上,两点之间的最短距离,就是经过这两点的大圆在这两点间的一段劣弧的长度,把这个弧长叫作两点的球面距离.
激趣诱思
知识点拨
微练习
一条直线被一个半径为13的球截得的线段长为24,则球心到直线的距离为( )
A.13 B.12 C.5 D.24
答案C
激趣诱思
知识点拨
二、圆柱、圆锥、圆台的定义及结构特征
1.定义
激趣诱思
知识点拨
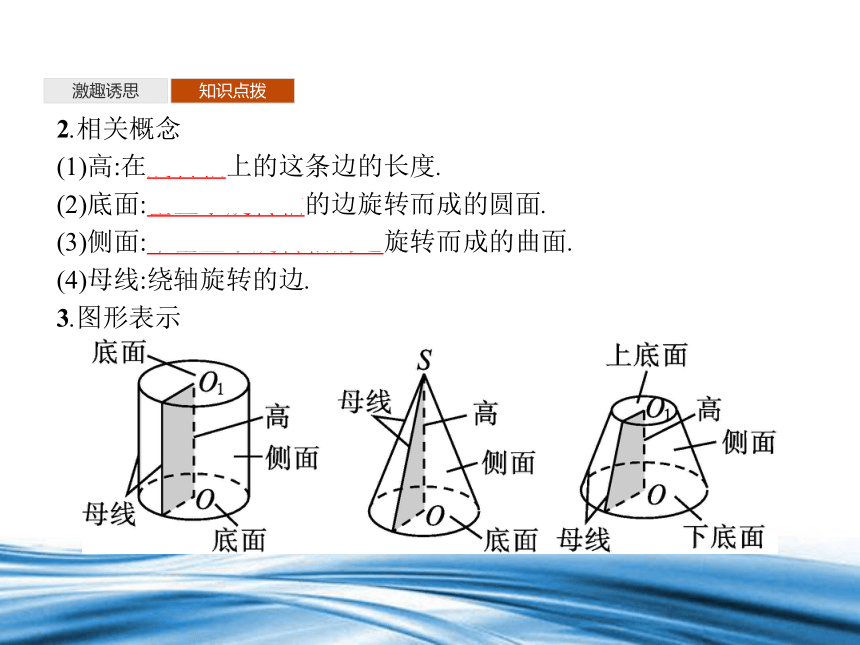
2.相关概念
(1)高:在旋转轴上的这条边的长度.
(2)底面:垂直于旋转轴的边旋转而成的圆面.
(3)侧面:不垂直于旋转轴的边旋转而成的曲面.
(4)母线:绕轴旋转的边.
3.图形表示
激趣诱思
知识点拨
微判断
判断(正确的打“√”,错误的打“×”).
(1)直角三角形绕一边所在直线旋转得到的旋转体是圆锥.( )
(2)圆锥截去一个小圆锥后剩余部分是圆台.( )
(3)夹在圆柱的两个平行截面间的几何体是一圆柱.( )
答案(1)× (2)√ (3)×
激趣诱思
知识点拨
微练习1
将一个等腰梯形绕着它的较长的底边所在直线旋转一周,所得的几何体包括( )
A.一个圆台、两个圆锥B.两个圆柱、一个圆锥
C.两个圆台、一个圆柱 D.一个圆柱、两个圆锥
解析图①是一个等腰梯形,CD为较长的底边,以CD边所在直线为旋转轴旋转一周所得几何体为一个组合体,如图②,包括一个圆柱、两个圆锥.
答案D
激趣诱思
知识点拨
名师点析 四种常见简单旋转体的性质比较
类型 球 圆 柱 圆 锥 圆 台
底面形状 无 两个底面是互相平行且半径相等的圆 圆 两个底面是互相平行且半径不相等的圆
母线 无 互相平行且长度相等 相交于顶点 且长度相等 延长线交于一点且长度相等
平行于 底面的 截面形状 无 与两个底面半径相等的圆 与底面半径 不相等的圆 与两个底面半径不相等的圆
过轴的截 面的形状 圆 矩形 等腰三角形 等腰梯形
激趣诱思
知识点拨
微练习2
如图所示的几何体是由哪个平面图形旋转得到的( )
解析图中所给的几何体是由上部的圆锥和下部的圆台组合而成的,故所求平面图形的上部是直角三角形,下部为直角梯形构成.
答案D
探究一
探究二
探究三
当堂检测
旋转体的结构特征
例1判断下列各说法是否正确.
(1)用一个平面去截圆锥,得到一个圆锥和圆台;
(2)一直角梯形绕下底所在直线旋转一周而形成的面所围成的几何体是圆台;
(3)圆锥、圆台中过轴的截面是轴截面,圆锥的轴截面是等腰三角形,圆台的轴截面是等腰梯形;
(4)到定点的距离等于定长的点的集合是球.
探究一
探究二
探究三
当堂检测
解(1)错.
只有在平面平行于圆锥底面时,才能将圆锥截为一个圆锥和一个圆台.
(2)错.直角梯形绕下底所在直线旋转一周所形成的几何体是由一个圆柱与一个圆锥组成的简单组合体,如图所示.
(3)正确.
(4)错.应为球面.
反思感悟 准确理解旋转体的定义,在此基础上掌握各旋转体的性质,才能更好地把握它们的结构特征,以作出准确的判断.
探究一
探究二
探究三
当堂检测
变式训练1给出下列说法:①经过圆柱任意两条母线的截面是一个矩形面;②圆台的任意两条母线的延长线,可能相交,也可能不相交;③圆柱上底面圆上任一点与下底面圆上任一点的连线都是圆柱的母线.其中说法正确的是 .(填序号)
解析①
正确,如图所示,经过圆柱任意两条母线的截面是一个矩形面;
②不正确,圆台的母线延长后必相交于一点;
③不正确,由圆柱母线的定义知,圆柱的母线应平行于轴.
答案①
探究一
探究二
探究三
当堂检测
球的截面问题
例2已知半径为25 cm的球的一个截面的面积是49π cm2,则球心到这个截面的距离为 .
解析设球的半径为R,截面圆的半径为r,球心到截面的距离为d.因为S截=πr2=49π,
所以r=7 cm,
即球心到这个截面的距离为24 cm.
答案24 cm
反思感悟 设球的截面圆上一点A,球心为O,截面圆心为O1,则△AO1O是以O1为直角顶点的直角三角形,解答球的截面问题时,常用该直角三角形或者用过球心和截面圆心的轴截面求解.
探究一
探究二
探究三
当堂检测
变式训练2半径是13 cm的球面上有A,B,C三点,并且AB=BC=CA=12 cm,试求球心到经过这三点的截面的距离.
解设截面圆的圆心为O1,球的球心为O,
则OO1即为球心到截面的距离,
又O1是正三角形ABC的外心,
所以球心到经过A,B,C三点的截面的距离为11 cm.
探究一
探究二
探究三
当堂检测
圆柱、圆锥、圆台中的有关计算
例3如图,用一个平行于圆锥SO底面的平面截这个圆锥,截得圆台上、下底面的面积之比为1∶16,截去的圆锥的母线长是3 cm,求圆台O'O的母线长.
解设圆台的母线长为l cm,由截得圆台上、下底面面积之比为1∶16,可设截得圆台的上、下底面的半径分别为r cm,4r cm.
过轴SO作截面,如图.
探究一
探究二
探究三
当堂检测
延伸探究本例中若圆台的上底面半径为1 cm,其他条件不变,试求圆台的高.
探究一
探究二
探究三
当堂检测
1.下列选项中的三角形绕直线l旋转一周,能得到如下图中的几何体的是( )
答案B
探究一
探究二
探究三
当堂检测
2.一正方体内接于一个球,经过球心作一个截面,则截面的可能图形为 .(只填写序号)
解析当截面平行于正方体的一个侧面时得①图;当截面过正方体的体对角线时得③图;当截面不平行于任何侧面也不过体对角线时得②图.
答案①②③
探究一
探究二
探究三
当堂检测
答案2
探究一
探究二
探究三
当堂检测
4.湖面上浮着一个球,湖水结冰后,将球取出,冰上留下一个直径为24 cm,深为8 cm的空穴,则球的半径为 cm.
解析设球的半径为R cm,
由题意知,截面圆的半径r=12 cm,截面圆圆心与球心的距离
d=(R-8)cm,由R2=r2+d2,得R2=144+(R-8)2,
即208-16R=0,解得R=13 cm.
答案13
6.1.3 简单旋转体——球、圆柱、圆锥和圆台
课标阐释
1.了解球、圆柱、圆锥、圆台的定义.(数学抽象)
2.掌握球、圆柱、圆锥、圆台的结构特征,并能在几何体中进行相关的计算.(几何直观、数学运算)
3.了解简单组合体的概念及结构特征.(几何直观)
思维脉络
激趣诱思
知识点拨
素描是艺术类考生必须掌握的基本功之一,素描如果按表现内容可分为静物、动物、风景、人像等,其中几何体的素描就属于静物素描的范畴.要画好素描静物,必须打好石膏几何体这个基础,其中空间想象能力是必不可少的.下图是一位考生的素描作品,它是组合体,你能从中找出两个旋转体吗 是怎样旋转而成的 这两个旋转体互相交叉的部分形状如何
激趣诱思
知识点拨
一、球
1.球的定义、相关概念、图形及表示
球及相关概念 图形及表示
定义 以半圆的直径所在的直线为旋转轴,将半圆旋转一周所形成的曲面称为球面,球面所围成的几何体称为球体,简称球 用表示球心的字母表示
图中的球记作:球O
相关 概念 球心:半圆的圆心称为球心 半径:连接球心和球面上任意一点的线段称为球的半径 直径:连接球面上两点并且过球心的线段称为球的直径
激趣诱思
知识点拨
2.球的相关性质
(1)球面上所有的点到球心的距离都等于球的半径.
(2)用任何一个平面去截球面,得到的截面都是圆,其中过球心的平面截球面得到的半径最大,等于球的半径.
微拓展
(1)球的大圆:球面被经过球心的平面截得的圆.
(2)球的小圆:球面被不经过球心的平面截得的圆.
(3)两点的球面距离:在球面上,两点之间的最短距离,就是经过这两点的大圆在这两点间的一段劣弧的长度,把这个弧长叫作两点的球面距离.
激趣诱思
知识点拨
微练习
一条直线被一个半径为13的球截得的线段长为24,则球心到直线的距离为( )
A.13 B.12 C.5 D.24
答案C
激趣诱思
知识点拨
二、圆柱、圆锥、圆台的定义及结构特征
1.定义
激趣诱思
知识点拨
2.相关概念
(1)高:在旋转轴上的这条边的长度.
(2)底面:垂直于旋转轴的边旋转而成的圆面.
(3)侧面:不垂直于旋转轴的边旋转而成的曲面.
(4)母线:绕轴旋转的边.
3.图形表示
激趣诱思
知识点拨
微判断
判断(正确的打“√”,错误的打“×”).
(1)直角三角形绕一边所在直线旋转得到的旋转体是圆锥.( )
(2)圆锥截去一个小圆锥后剩余部分是圆台.( )
(3)夹在圆柱的两个平行截面间的几何体是一圆柱.( )
答案(1)× (2)√ (3)×
激趣诱思
知识点拨
微练习1
将一个等腰梯形绕着它的较长的底边所在直线旋转一周,所得的几何体包括( )
A.一个圆台、两个圆锥B.两个圆柱、一个圆锥
C.两个圆台、一个圆柱 D.一个圆柱、两个圆锥
解析图①是一个等腰梯形,CD为较长的底边,以CD边所在直线为旋转轴旋转一周所得几何体为一个组合体,如图②,包括一个圆柱、两个圆锥.
答案D
激趣诱思
知识点拨
名师点析 四种常见简单旋转体的性质比较
类型 球 圆 柱 圆 锥 圆 台
底面形状 无 两个底面是互相平行且半径相等的圆 圆 两个底面是互相平行且半径不相等的圆
母线 无 互相平行且长度相等 相交于顶点 且长度相等 延长线交于一点且长度相等
平行于 底面的 截面形状 无 与两个底面半径相等的圆 与底面半径 不相等的圆 与两个底面半径不相等的圆
过轴的截 面的形状 圆 矩形 等腰三角形 等腰梯形
激趣诱思
知识点拨
微练习2
如图所示的几何体是由哪个平面图形旋转得到的( )
解析图中所给的几何体是由上部的圆锥和下部的圆台组合而成的,故所求平面图形的上部是直角三角形,下部为直角梯形构成.
答案D
探究一
探究二
探究三
当堂检测
旋转体的结构特征
例1判断下列各说法是否正确.
(1)用一个平面去截圆锥,得到一个圆锥和圆台;
(2)一直角梯形绕下底所在直线旋转一周而形成的面所围成的几何体是圆台;
(3)圆锥、圆台中过轴的截面是轴截面,圆锥的轴截面是等腰三角形,圆台的轴截面是等腰梯形;
(4)到定点的距离等于定长的点的集合是球.
探究一
探究二
探究三
当堂检测
解(1)错.
只有在平面平行于圆锥底面时,才能将圆锥截为一个圆锥和一个圆台.
(2)错.直角梯形绕下底所在直线旋转一周所形成的几何体是由一个圆柱与一个圆锥组成的简单组合体,如图所示.
(3)正确.
(4)错.应为球面.
反思感悟 准确理解旋转体的定义,在此基础上掌握各旋转体的性质,才能更好地把握它们的结构特征,以作出准确的判断.
探究一
探究二
探究三
当堂检测
变式训练1给出下列说法:①经过圆柱任意两条母线的截面是一个矩形面;②圆台的任意两条母线的延长线,可能相交,也可能不相交;③圆柱上底面圆上任一点与下底面圆上任一点的连线都是圆柱的母线.其中说法正确的是 .(填序号)
解析①
正确,如图所示,经过圆柱任意两条母线的截面是一个矩形面;
②不正确,圆台的母线延长后必相交于一点;
③不正确,由圆柱母线的定义知,圆柱的母线应平行于轴.
答案①
探究一
探究二
探究三
当堂检测
球的截面问题
例2已知半径为25 cm的球的一个截面的面积是49π cm2,则球心到这个截面的距离为 .
解析设球的半径为R,截面圆的半径为r,球心到截面的距离为d.因为S截=πr2=49π,
所以r=7 cm,
即球心到这个截面的距离为24 cm.
答案24 cm
反思感悟 设球的截面圆上一点A,球心为O,截面圆心为O1,则△AO1O是以O1为直角顶点的直角三角形,解答球的截面问题时,常用该直角三角形或者用过球心和截面圆心的轴截面求解.
探究一
探究二
探究三
当堂检测
变式训练2半径是13 cm的球面上有A,B,C三点,并且AB=BC=CA=12 cm,试求球心到经过这三点的截面的距离.
解设截面圆的圆心为O1,球的球心为O,
则OO1即为球心到截面的距离,
又O1是正三角形ABC的外心,
所以球心到经过A,B,C三点的截面的距离为11 cm.
探究一
探究二
探究三
当堂检测
圆柱、圆锥、圆台中的有关计算
例3如图,用一个平行于圆锥SO底面的平面截这个圆锥,截得圆台上、下底面的面积之比为1∶16,截去的圆锥的母线长是3 cm,求圆台O'O的母线长.
解设圆台的母线长为l cm,由截得圆台上、下底面面积之比为1∶16,可设截得圆台的上、下底面的半径分别为r cm,4r cm.
过轴SO作截面,如图.
探究一
探究二
探究三
当堂检测
延伸探究本例中若圆台的上底面半径为1 cm,其他条件不变,试求圆台的高.
探究一
探究二
探究三
当堂检测
1.下列选项中的三角形绕直线l旋转一周,能得到如下图中的几何体的是( )
答案B
探究一
探究二
探究三
当堂检测
2.一正方体内接于一个球,经过球心作一个截面,则截面的可能图形为 .(只填写序号)
解析当截面平行于正方体的一个侧面时得①图;当截面过正方体的体对角线时得③图;当截面不平行于任何侧面也不过体对角线时得②图.
答案①②③
探究一
探究二
探究三
当堂检测
答案2
探究一
探究二
探究三
当堂检测
4.湖面上浮着一个球,湖水结冰后,将球取出,冰上留下一个直径为24 cm,深为8 cm的空穴,则球的半径为 cm.
解析设球的半径为R cm,
由题意知,截面圆的半径r=12 cm,截面圆圆心与球心的距离
d=(R-8)cm,由R2=r2+d2,得R2=144+(R-8)2,
即208-16R=0,解得R=13 cm.
答案13
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
