沪粤版九年级上册物理 14.2探究欧姆定律 第2课时串、并联电路的计算 习题课件 (共15张PPT)
文档属性
| 名称 | 沪粤版九年级上册物理 14.2探究欧姆定律 第2课时串、并联电路的计算 习题课件 (共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 235.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪粤版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-23 00:00:00 | ||
图片预览



文档简介
(共15张PPT)
第十四章 探究欧姆定律
14.2 探究欧姆定律
第2课时 串、并联电路的计算
夯实基础
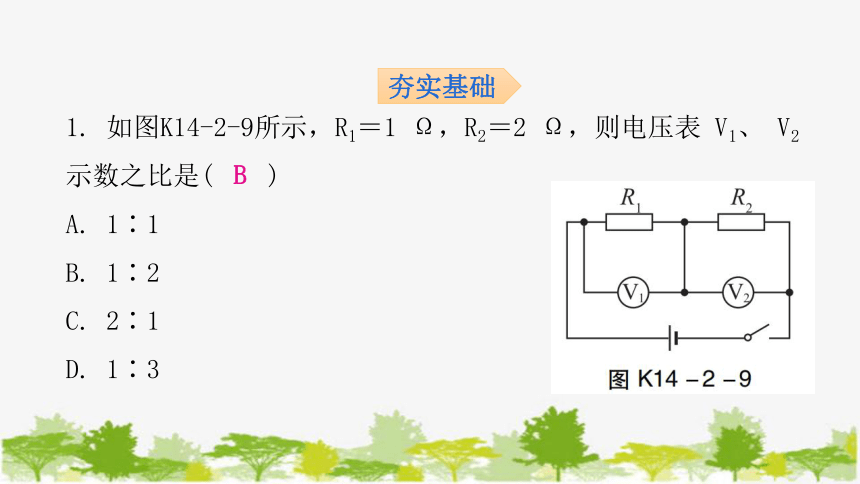
1. 如图K14-2-9所示,R1=1 Ω,R2=2 Ω,则电压表 V1、 V2示数之比是( )
A. 1∶1
B. 1∶2
C. 2∶1
D. 1∶3
B
2. 如图K14-2-10所示,灯泡L1、L2的电阻分别为200 Ω和300 Ω,闭合开关S,通过灯泡L1、L2的电流分别为I1、I2,它们两端的电压分别为U1、U2,则下列正确的是( )
A.I1∶I2=2∶3,U1∶U2=1:1
B.I1∶I2=3∶2,U1∶U2=1:1
C.I1∶I2=1∶1,U1∶U2=2:3
D.I1∶I2=1∶1,U1∶U2=3∶2
B
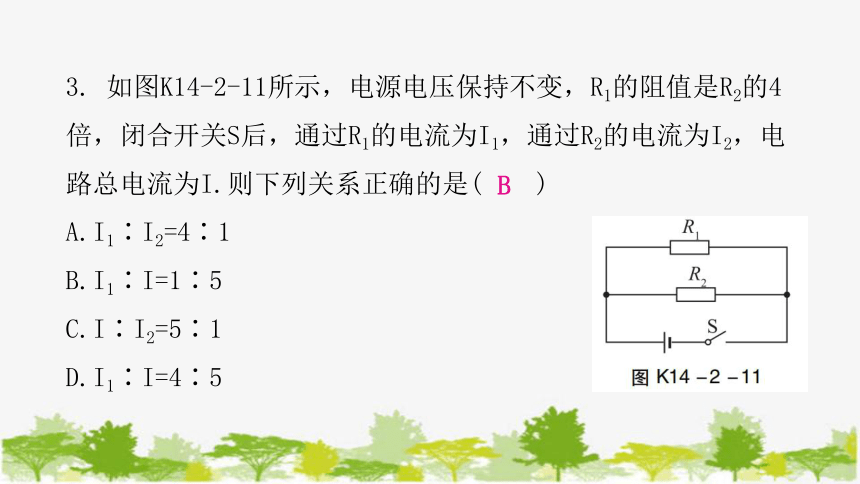
3. 如图K14-2-11所示,电源电压保持不变,R1的阻值是R2的4倍,闭合开关S后,通过R1的电流为I1,通过R2的电流为I2,电路总电流为I.则下列关系正确的是( )
A.I1∶I2=4∶1
B.I1∶I=1∶5
C.I∶I2=5∶1
D.I1∶I=4∶5
B
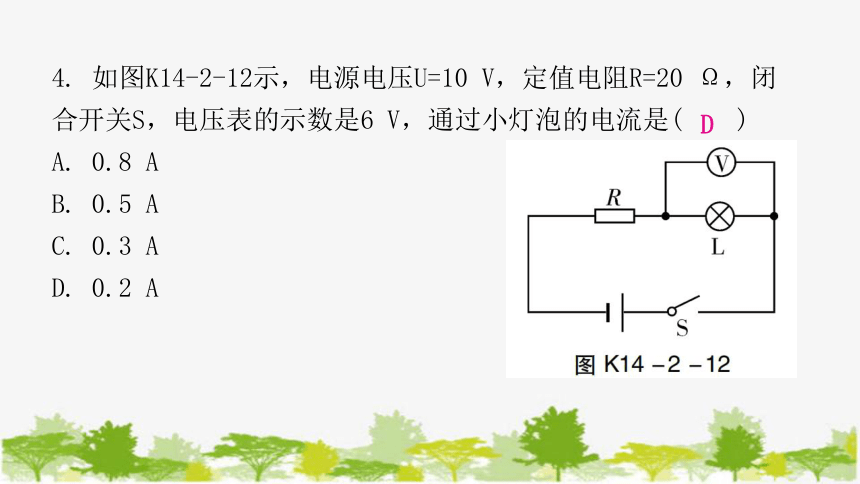
4. 如图K14-2-12示,电源电压U=10 V,定值电阻R=20 Ω,闭合开关S,电压表的示数是6 V,通过小灯泡的电流是( )
A. 0.8 A
B. 0.5 A
C. 0.3 A
D. 0.2 A
D
5. 小敏在探究串、并联电路的电流、电压、电阻之间的关系时,用了两个阻值不同的电阻R1、R2,它们的阻值之比是5∶3,如果它们串联在电路中,则电阻两端的电压之比为________;如果把它们并联在电路中,则通过电阻的电流之比为________。
5∶3
3∶5
0.2 A
6 V
30 Ω
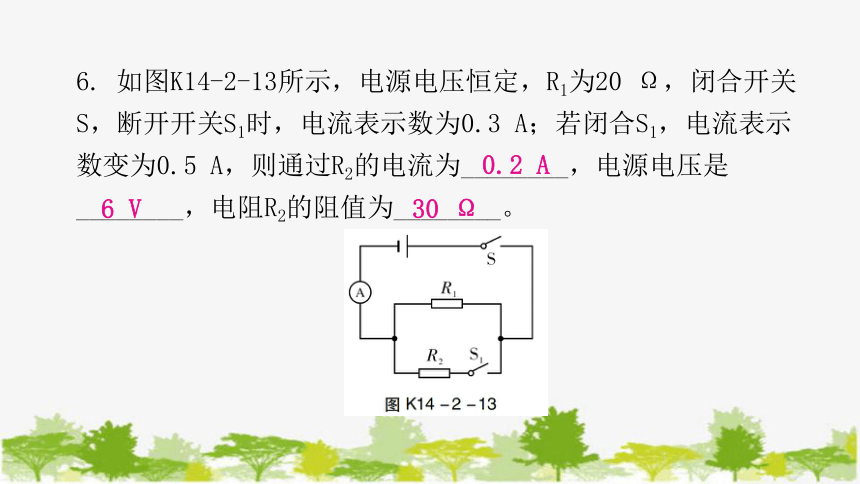
6. 如图K14-2-13所示,电源电压恒定,R1为20 Ω,闭合开关S,断开开关S1时,电流表示数为0.3 A;若闭合S1,电流表示数变为0.5 A,则通过R2的电流为________,电源电压是________,电阻R2的阻值为________。
7. 如图K14-2-14所示,当电源电压为4 V时,电压表的示数为1 V;当电源电压增加到12 V时,电流表的示数为1 A。则电阻R1=________Ω,R2=________Ω。
9
3
8. 如图K14-2-15所示,把10 Ω的电阻R1和15 Ω的电阻R2并联起来。闭合开关S后,电流表的示数为0.2 A。求:
(1)电源电压。
(2)通过电阻R1的电流。
解:(1)U2=I2R2=0.2 A×15 Ω=3 V,因为R1与R2并联,所以U=U1=U2=3 V。
(2)I1= =0.3 A。
答:(1)电源电压为3 V。
(2)通过电阻R1的电流为0.3 A。
9. 小林用一个电流表和一个阻值为10 Ω的电阻R0来测某未知电阻Rx的阻值,设计了如图K14-2-16所示的电路,在只闭合S的情况下,电流表的示数为0.6 A;在同时闭合S、S1时,电流表的示数为0.9 A,电源电压不变,求:
(1)电源电压。
(2)电阻Rx的阻值。
解:(1)只闭合S时,电路为R0的简单电路,电流表测通过R0的电流,由I= 可得,电源的电压U=I0R0=0.6 A×10 Ω=6 V。
(2)同时闭合S、S1时,R0与Rx并联,电流表测干路电流,所以,通过Rx的电流
Ix=I-I0=0.9 A-0.6 A=0.3 A,
所以Rx= =20 Ω。
答:(1)电源电压为6 V。
(2)电阻Rx的阻值为20 Ω。
能力提升
10. 在相距50 km的甲、乙两地间沿直线架设两条输电线。输电线的电阻与其长度成正比,若输电线在某处发生了短路,为确定短路位置,甲、乙两地的检修员用输出电压相同且不变的电源和电流表做成如图K14-2-17所示的测量仪,并分别进行了如下测量:将测量仪连接a、b时,电流表
的示数为1.2 A;将测量仪连接c、d时,电
流表的示数为0.3 A,由此可判断短路位置
离甲地的距离是( )
A. 10 km B. 20 km
C. 30 km D. 40 km
A
11. 甲电阻标有“10 Ω 1 A”字样,乙电阻标有“20 Ω 0.6 A”字样,将两个电阻串联起来,电路中允许通过的最大电流是________A;电源电压最大为________V;如果将两个电阻并联起来,电源电压最大为________V;此时干路电流是________A。
0.6
18
10
1.5
第十四章 探究欧姆定律
14.2 探究欧姆定律
第2课时 串、并联电路的计算
夯实基础
1. 如图K14-2-9所示,R1=1 Ω,R2=2 Ω,则电压表 V1、 V2示数之比是( )
A. 1∶1
B. 1∶2
C. 2∶1
D. 1∶3
B
2. 如图K14-2-10所示,灯泡L1、L2的电阻分别为200 Ω和300 Ω,闭合开关S,通过灯泡L1、L2的电流分别为I1、I2,它们两端的电压分别为U1、U2,则下列正确的是( )
A.I1∶I2=2∶3,U1∶U2=1:1
B.I1∶I2=3∶2,U1∶U2=1:1
C.I1∶I2=1∶1,U1∶U2=2:3
D.I1∶I2=1∶1,U1∶U2=3∶2
B
3. 如图K14-2-11所示,电源电压保持不变,R1的阻值是R2的4倍,闭合开关S后,通过R1的电流为I1,通过R2的电流为I2,电路总电流为I.则下列关系正确的是( )
A.I1∶I2=4∶1
B.I1∶I=1∶5
C.I∶I2=5∶1
D.I1∶I=4∶5
B
4. 如图K14-2-12示,电源电压U=10 V,定值电阻R=20 Ω,闭合开关S,电压表的示数是6 V,通过小灯泡的电流是( )
A. 0.8 A
B. 0.5 A
C. 0.3 A
D. 0.2 A
D
5. 小敏在探究串、并联电路的电流、电压、电阻之间的关系时,用了两个阻值不同的电阻R1、R2,它们的阻值之比是5∶3,如果它们串联在电路中,则电阻两端的电压之比为________;如果把它们并联在电路中,则通过电阻的电流之比为________。
5∶3
3∶5
0.2 A
6 V
30 Ω
6. 如图K14-2-13所示,电源电压恒定,R1为20 Ω,闭合开关S,断开开关S1时,电流表示数为0.3 A;若闭合S1,电流表示数变为0.5 A,则通过R2的电流为________,电源电压是________,电阻R2的阻值为________。
7. 如图K14-2-14所示,当电源电压为4 V时,电压表的示数为1 V;当电源电压增加到12 V时,电流表的示数为1 A。则电阻R1=________Ω,R2=________Ω。
9
3
8. 如图K14-2-15所示,把10 Ω的电阻R1和15 Ω的电阻R2并联起来。闭合开关S后,电流表的示数为0.2 A。求:
(1)电源电压。
(2)通过电阻R1的电流。
解:(1)U2=I2R2=0.2 A×15 Ω=3 V,因为R1与R2并联,所以U=U1=U2=3 V。
(2)I1= =0.3 A。
答:(1)电源电压为3 V。
(2)通过电阻R1的电流为0.3 A。
9. 小林用一个电流表和一个阻值为10 Ω的电阻R0来测某未知电阻Rx的阻值,设计了如图K14-2-16所示的电路,在只闭合S的情况下,电流表的示数为0.6 A;在同时闭合S、S1时,电流表的示数为0.9 A,电源电压不变,求:
(1)电源电压。
(2)电阻Rx的阻值。
解:(1)只闭合S时,电路为R0的简单电路,电流表测通过R0的电流,由I= 可得,电源的电压U=I0R0=0.6 A×10 Ω=6 V。
(2)同时闭合S、S1时,R0与Rx并联,电流表测干路电流,所以,通过Rx的电流
Ix=I-I0=0.9 A-0.6 A=0.3 A,
所以Rx= =20 Ω。
答:(1)电源电压为6 V。
(2)电阻Rx的阻值为20 Ω。
能力提升
10. 在相距50 km的甲、乙两地间沿直线架设两条输电线。输电线的电阻与其长度成正比,若输电线在某处发生了短路,为确定短路位置,甲、乙两地的检修员用输出电压相同且不变的电源和电流表做成如图K14-2-17所示的测量仪,并分别进行了如下测量:将测量仪连接a、b时,电流表
的示数为1.2 A;将测量仪连接c、d时,电
流表的示数为0.3 A,由此可判断短路位置
离甲地的距离是( )
A. 10 km B. 20 km
C. 30 km D. 40 km
A
11. 甲电阻标有“10 Ω 1 A”字样,乙电阻标有“20 Ω 0.6 A”字样,将两个电阻串联起来,电路中允许通过的最大电流是________A;电源电压最大为________V;如果将两个电阻并联起来,电源电压最大为________V;此时干路电流是________A。
0.6
18
10
1.5
同课章节目录
- 第十一章 机械功与机械能
- 11.1 怎样才叫做功
- 11.2 怎样比较做功的快慢
- 11.3 如何提高机械效率
- 11.4 认识动能和势能
- 第十二章 内能与热机
- 12.1 认识内能
- 12.2 热量和热值
- 12.3 研究物质的比热容
- 12.4 热机与社会发展
- 第十三章 探究简单电路
- 13.1 从闪电谈起
- 13.2 电路的组成和连接方式
- 13.3 怎样认识和测量电流
- 13.4 探究串、并联电路中的电流
- 13.5 怎样认识和测量电压
- 13.6 探究串、并联电路中的电压
- 第十四章 探究欧姆定律
- 14.1 怎样认识电阻
- 14.2 探究欧姆定律
- 14.3 欧姆定律的应用
- 第十五章 电能与电功率
- 15.1 电能与电功
- 15.2 认识电功率
- 15.3 怎样使用电器正常工作
- 15.4 探究焦耳定律
