高中数学人教A版(2019)必修 第二册第八章 立体几何初步8.6.2 直线与平面垂直1(共24张PPT)
文档属性
| 名称 | 高中数学人教A版(2019)必修 第二册第八章 立体几何初步8.6.2 直线与平面垂直1(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-24 11:27:43 | ||
图片预览







文档简介
(共24张PPT)
8.6.2直线与平面垂直
定义 前提 两条异面直线a,b
作法 经过空间任一点O作直线a′∥a,b′∥b
结论 我们把a′与b′所成的 叫做异面直线a与b所成的角(或夹角)
范围 记异面直线a与b所成的角为θ,则___________
特殊情况 当θ=_____时,a与b互相垂直,记作______
锐角(或直角)
0°<θ≤90°
90°
a⊥b
复习回顾
异面直线所成角
3、求异面直线的所成角的一般步骤是:作—证—求
作出异面直线所成的角,可通过多种方法平移产生,主要有三种方法:
①直接平移法(可利用图中已有的平行线);
②中位线平移法;
③补形平移法(在已知图形中,补作一个相同的几何体,以便找到平行线).
问题1:请同学们观察图片,说出旗杆与地面、
大桥桥柱与水面是什么位置关系?
你能举出一些类似的例子吗?
A
B
α
B1
C1
C
B
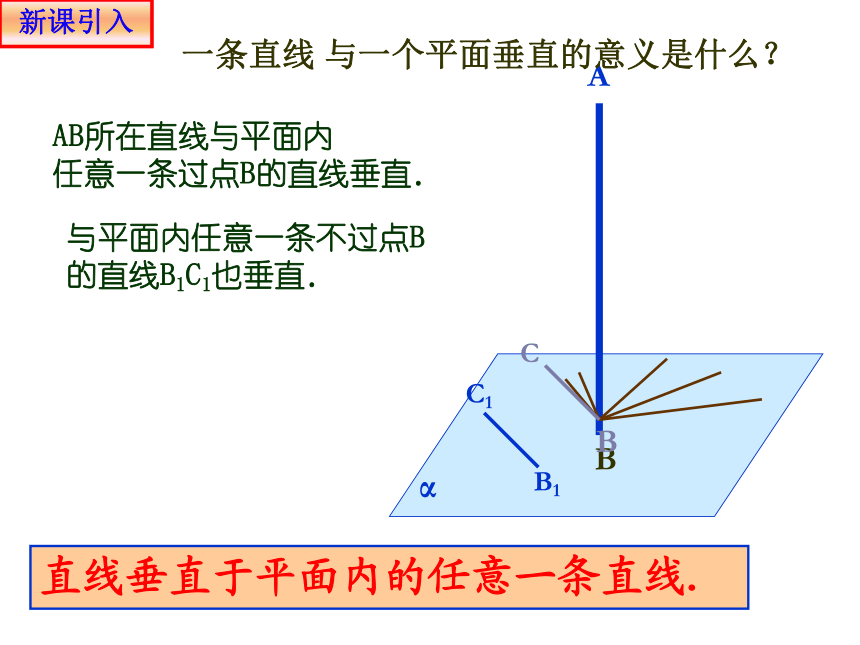
一条直线 与一个平面垂直的意义是什么?
新课引入
AB所在直线与平面内
任意一条过点B的直线垂直.
与平面内任意一条不过点B的直线B1C1也垂直.
直线垂直于平面内的任意一条直线.
(一)直线与平面垂直的定义
如果直线 l和平面α内的任意一条直线都垂直,我们就说直线 l 和平面α互相垂直.记作l⊥α
直线l叫做平面α的垂线, 平面α叫做直线 l的垂面,
直线 和平面垂直,它们唯一的公共点P叫做垂足.
α
l
P
(性质定理)
b是平面α内任一直线,a⊥α,则 .
a⊥b
学习新知
符号语言:任意a α,都有l⊥a .
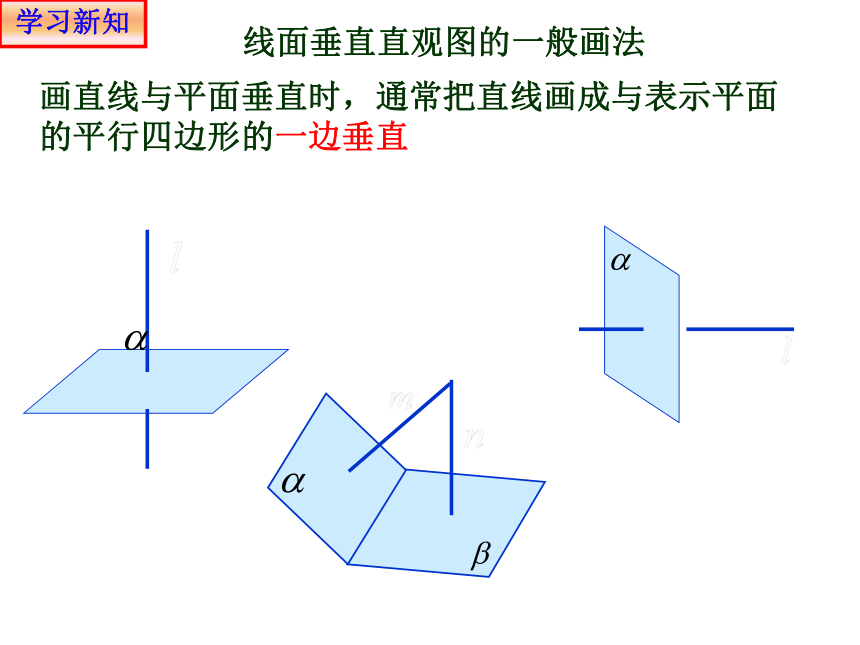
画直线与平面垂直时,通常把直线画成与表示平面的平行四边形的一边垂直
线面垂直直观图的一般画法
学习新知
思考:在同一平面内,过一点有且只有一条直线与已知直线垂直.将这一结论推广到空间,过一点垂直于已知平面的直线有几条?为什么?
可以发现:过一点垂直于已知平面的直线有且只有一条.
过一点作垂直于已知平面的直线,则该点与垂足间的线段,叫做这个点到该平面的垂线段,垂线段的长度叫做这个点到该平面的距离.
点到平面的距离
如棱锥的高就是顶点到底面的距离.
学习新知
1、如果一条直线垂直于平面内的一条直线,能否判断这条直线和这个平面垂直?
2、如果一条直线垂直于平面内的两条直线,能否判断这条直线和这个平面垂直?
3、如果一条直线垂直于平面内的无数条直线,能否判断这条直线和这个平面垂直?
怎样判断线面垂直呢?
学习新知
不一定.当平面α内的无数条直线a,b,c…都互相平行时,直线l在保证与直线a,b,c…都垂直的条件下,与平面α可能垂直也可能斜交.
D
B
A
C
容易发现,当且仅当折痕AD是BC边上的高时,AD所在直线与桌面所在平面α垂直。
a
B
D
C
A
(1)有人说,折痕AD所在直线与桌面所在平面α上的一条直线垂直,就可以判断AD垂直平面α,你同意他的说法吗
(2)折痕AD⊥BC,翻折之后垂直关系不变,即AD ⊥ CD,AD ⊥ BD,由此你能得到什么结论
学习新知
判定定理
如果一条直线和一个平面内的两条相交
直线都垂直,那么这条直线垂直于这个平面.
B
m
n
l
α
学习新知
例1、有一根旗杆AB高8m,它的顶端A挂有一条长10m的绳子,拉紧绳子并把它的下端放在地面上的两点(和旗杆脚不在同一条直线上)C、D,如果这两点都和旗杆脚B的距离是6m,那么旗杆就和地面垂直,为什么?
A
B
C
D
典型例题
V
A
B
C
.
D
巩固练习
m
a
b
例2、求证:如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面
n
典型例题
已知:如图,已知a∥b,a⊥α.
求证:b⊥α.
分析:在平面内作两条相交直线,由直线与平面垂直的定义可知,直线a与这两条相交直线是垂直的,又由b平行a,可证b与这两条相交直线也垂直,从而可证直线与平面垂直.
证明:在平面α内取两条相交直线m、n,
E
A
B
C
D
巩固练习
2 、如果平面外的一条直线上有两点到这个平面的
距离相等,则这条直线和平面的位置关系是( )
A.平行 B.相交 C.平行或相交
3、在空间,下列命题
(1)平行于同一直线的两条直线互相平行;
(2)垂直于同一直线的两条直线互相平行;
(3)平行于同一平面的两条直线互相平行;
(4)垂直于同一平面的两条直线互相平行。
正确的是( )
A.(1)(3)(4) B.(1)(4) C.(1) D.(1)(2)(3)(4)
C
B
巩固练习
证明:(1)因为SA=SC,D为AC的中点,
所以SD⊥AC.
则在Rt△ABC中,
有AD=DC=BD,所以△ADS≌△BDS.
所以∠BDS=∠ADS=90°,即SD⊥BD.
又AC∩BD=D,AC,BD 平面ABC,
所以SD⊥平面ABC.
典型例题
典型例题
[证明] (2)因为AB=BC,D为AC的中点,
所以BD⊥AC.
又由(1)知SD⊥BD
于是BD垂直于平面SAC内的两条相交直线
所以BD⊥平面SAC.
判定直线与平面垂直,可以用定义,就是证明这条直线与平面内的任一直线垂直,但这种方法一般不用.最常用也最好用的是直线与平面垂直的判定定理,根据定理,只需证明这条直线与平面内的两条相交直线垂直即可.
另外,判定直线与平面垂直还有如下两个结论可用:
(1)两条平行直线中的一条垂直于一个平面,则另一条也垂直于这个平面.
(2)若一条直线与两平行平面中的一个面垂直,则它与另
一个平面也垂直.
方法总结
例4如图,已知PA垂直于☉O所在的平面,AB是☉O的直径,C是☉O上任意一点,求证:BC⊥PC.
分析:首先利用PA⊥平面ABC得到PA⊥BC,然后根据圆的性质得到AC⊥BC,进而利用线面垂直判定定理证得BC⊥平面PAC,从而得到BC⊥PC.
证明:∵PA⊥平面ABC,BC 平面ABC,∴PA⊥BC.
∵AB是☉O的直径,∴BC⊥AC.
又PA∩AC=A,∴BC⊥平面PAC.
∵PC 平面PAC,∴BC⊥PC.
变式:若本例中其他条件不变,
作AE⊥PC交PC于点E,求证:AE⊥PB.
典型例题
直线和平面垂直的定义具有双重作用:判定和性质.
判定是指:如果一条直线和平面内的任意一条直线都垂直,那么直线就与平面垂直;
性质是指:如果一条直线垂直于一个平面,那么这条直线就垂直于平面内的任意一条直线,即a⊥α,b α a⊥b.
由直线与平面垂直的定义及判定定理,就可以由线线垂直得到线面垂直,再由线面垂直得到线线垂直,即得到线线垂直与线面垂直的相互转化.因此,要证明两条直线垂直(无论它们是异面还是共面),通常是证明其中的一条直线垂直于另一条直线所在的一个平面.
反思感悟
思考探究
总结:证明线线垂直的方法
1、直线与平面垂直的定义
2、直线与平面垂直的判定与性质
课堂小结
8.6.2直线与平面垂直
定义 前提 两条异面直线a,b
作法 经过空间任一点O作直线a′∥a,b′∥b
结论 我们把a′与b′所成的 叫做异面直线a与b所成的角(或夹角)
范围 记异面直线a与b所成的角为θ,则___________
特殊情况 当θ=_____时,a与b互相垂直,记作______
锐角(或直角)
0°<θ≤90°
90°
a⊥b
复习回顾
异面直线所成角
3、求异面直线的所成角的一般步骤是:作—证—求
作出异面直线所成的角,可通过多种方法平移产生,主要有三种方法:
①直接平移法(可利用图中已有的平行线);
②中位线平移法;
③补形平移法(在已知图形中,补作一个相同的几何体,以便找到平行线).
问题1:请同学们观察图片,说出旗杆与地面、
大桥桥柱与水面是什么位置关系?
你能举出一些类似的例子吗?
A
B
α
B1
C1
C
B
一条直线 与一个平面垂直的意义是什么?
新课引入
AB所在直线与平面内
任意一条过点B的直线垂直.
与平面内任意一条不过点B的直线B1C1也垂直.
直线垂直于平面内的任意一条直线.
(一)直线与平面垂直的定义
如果直线 l和平面α内的任意一条直线都垂直,我们就说直线 l 和平面α互相垂直.记作l⊥α
直线l叫做平面α的垂线, 平面α叫做直线 l的垂面,
直线 和平面垂直,它们唯一的公共点P叫做垂足.
α
l
P
(性质定理)
b是平面α内任一直线,a⊥α,则 .
a⊥b
学习新知
符号语言:任意a α,都有l⊥a .
画直线与平面垂直时,通常把直线画成与表示平面的平行四边形的一边垂直
线面垂直直观图的一般画法
学习新知
思考:在同一平面内,过一点有且只有一条直线与已知直线垂直.将这一结论推广到空间,过一点垂直于已知平面的直线有几条?为什么?
可以发现:过一点垂直于已知平面的直线有且只有一条.
过一点作垂直于已知平面的直线,则该点与垂足间的线段,叫做这个点到该平面的垂线段,垂线段的长度叫做这个点到该平面的距离.
点到平面的距离
如棱锥的高就是顶点到底面的距离.
学习新知
1、如果一条直线垂直于平面内的一条直线,能否判断这条直线和这个平面垂直?
2、如果一条直线垂直于平面内的两条直线,能否判断这条直线和这个平面垂直?
3、如果一条直线垂直于平面内的无数条直线,能否判断这条直线和这个平面垂直?
怎样判断线面垂直呢?
学习新知
不一定.当平面α内的无数条直线a,b,c…都互相平行时,直线l在保证与直线a,b,c…都垂直的条件下,与平面α可能垂直也可能斜交.
D
B
A
C
容易发现,当且仅当折痕AD是BC边上的高时,AD所在直线与桌面所在平面α垂直。
a
B
D
C
A
(1)有人说,折痕AD所在直线与桌面所在平面α上的一条直线垂直,就可以判断AD垂直平面α,你同意他的说法吗
(2)折痕AD⊥BC,翻折之后垂直关系不变,即AD ⊥ CD,AD ⊥ BD,由此你能得到什么结论
学习新知
判定定理
如果一条直线和一个平面内的两条相交
直线都垂直,那么这条直线垂直于这个平面.
B
m
n
l
α
学习新知
例1、有一根旗杆AB高8m,它的顶端A挂有一条长10m的绳子,拉紧绳子并把它的下端放在地面上的两点(和旗杆脚不在同一条直线上)C、D,如果这两点都和旗杆脚B的距离是6m,那么旗杆就和地面垂直,为什么?
A
B
C
D
典型例题
V
A
B
C
.
D
巩固练习
m
a
b
例2、求证:如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面
n
典型例题
已知:如图,已知a∥b,a⊥α.
求证:b⊥α.
分析:在平面内作两条相交直线,由直线与平面垂直的定义可知,直线a与这两条相交直线是垂直的,又由b平行a,可证b与这两条相交直线也垂直,从而可证直线与平面垂直.
证明:在平面α内取两条相交直线m、n,
E
A
B
C
D
巩固练习
2 、如果平面外的一条直线上有两点到这个平面的
距离相等,则这条直线和平面的位置关系是( )
A.平行 B.相交 C.平行或相交
3、在空间,下列命题
(1)平行于同一直线的两条直线互相平行;
(2)垂直于同一直线的两条直线互相平行;
(3)平行于同一平面的两条直线互相平行;
(4)垂直于同一平面的两条直线互相平行。
正确的是( )
A.(1)(3)(4) B.(1)(4) C.(1) D.(1)(2)(3)(4)
C
B
巩固练习
证明:(1)因为SA=SC,D为AC的中点,
所以SD⊥AC.
则在Rt△ABC中,
有AD=DC=BD,所以△ADS≌△BDS.
所以∠BDS=∠ADS=90°,即SD⊥BD.
又AC∩BD=D,AC,BD 平面ABC,
所以SD⊥平面ABC.
典型例题
典型例题
[证明] (2)因为AB=BC,D为AC的中点,
所以BD⊥AC.
又由(1)知SD⊥BD
于是BD垂直于平面SAC内的两条相交直线
所以BD⊥平面SAC.
判定直线与平面垂直,可以用定义,就是证明这条直线与平面内的任一直线垂直,但这种方法一般不用.最常用也最好用的是直线与平面垂直的判定定理,根据定理,只需证明这条直线与平面内的两条相交直线垂直即可.
另外,判定直线与平面垂直还有如下两个结论可用:
(1)两条平行直线中的一条垂直于一个平面,则另一条也垂直于这个平面.
(2)若一条直线与两平行平面中的一个面垂直,则它与另
一个平面也垂直.
方法总结
例4如图,已知PA垂直于☉O所在的平面,AB是☉O的直径,C是☉O上任意一点,求证:BC⊥PC.
分析:首先利用PA⊥平面ABC得到PA⊥BC,然后根据圆的性质得到AC⊥BC,进而利用线面垂直判定定理证得BC⊥平面PAC,从而得到BC⊥PC.
证明:∵PA⊥平面ABC,BC 平面ABC,∴PA⊥BC.
∵AB是☉O的直径,∴BC⊥AC.
又PA∩AC=A,∴BC⊥平面PAC.
∵PC 平面PAC,∴BC⊥PC.
变式:若本例中其他条件不变,
作AE⊥PC交PC于点E,求证:AE⊥PB.
典型例题
直线和平面垂直的定义具有双重作用:判定和性质.
判定是指:如果一条直线和平面内的任意一条直线都垂直,那么直线就与平面垂直;
性质是指:如果一条直线垂直于一个平面,那么这条直线就垂直于平面内的任意一条直线,即a⊥α,b α a⊥b.
由直线与平面垂直的定义及判定定理,就可以由线线垂直得到线面垂直,再由线面垂直得到线线垂直,即得到线线垂直与线面垂直的相互转化.因此,要证明两条直线垂直(无论它们是异面还是共面),通常是证明其中的一条直线垂直于另一条直线所在的一个平面.
反思感悟
思考探究
总结:证明线线垂直的方法
1、直线与平面垂直的定义
2、直线与平面垂直的判定与性质
课堂小结
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
