8.6.3 平面与平面垂直(第1课时)课件(21张PPT)
文档属性
| 名称 | 8.6.3 平面与平面垂直(第1课时)课件(21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 512.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-24 13:25:01 | ||
图片预览






文档简介
(共21张PPT)
人教2019版必修第一册
第八章 立体几何初步
8.6.3 平面与平面垂直
第1课时 平面与平面垂直的判定
学习目标
1.理解二面角的概念,并会求简单的二面角;
2.理解直二面角与面面垂直的关系,理解平面和平面垂直的判定定理并能运用其解决相关问题.
3. 通过面面垂直定理的理解及运用,培养学生的空间转化能力和逻辑推理能力.
自主预习,回答问题
阅读课本155-158页,思考并完成以下问题
1、什么是二面角?什么是直二面角?
2、平面与平面平行的判定定理是什么?
3、怎样用符号语言表示平面与平面平行的判定定理?
要求:学生独立完成,以小组为单位,组内可商量,最终选出代表回答问题。
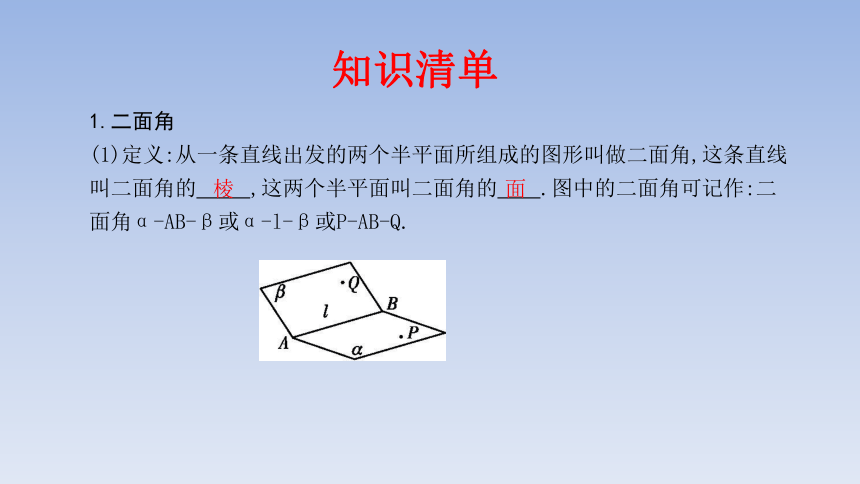
1.二面角
(1)定义:从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫二面角的 ,这两个半平面叫二面角的 .图中的二面角可记作:二面角α-AB-β或α-l-β或P-AB-Q.
棱
面
知识清单
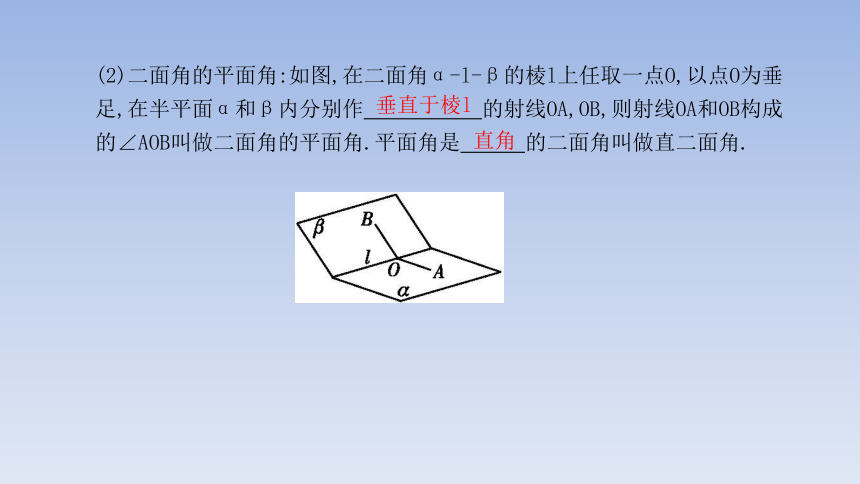
(2)二面角的平面角:如图,在二面角α-l-β的棱l上任取一点O,以点O为垂足,在半平面α和β内分别作 的射线OA,OB,则射线OA和OB构成的∠AOB叫做二面角的平面角.平面角是 的二面角叫做直二面角.
垂直于棱l
直角
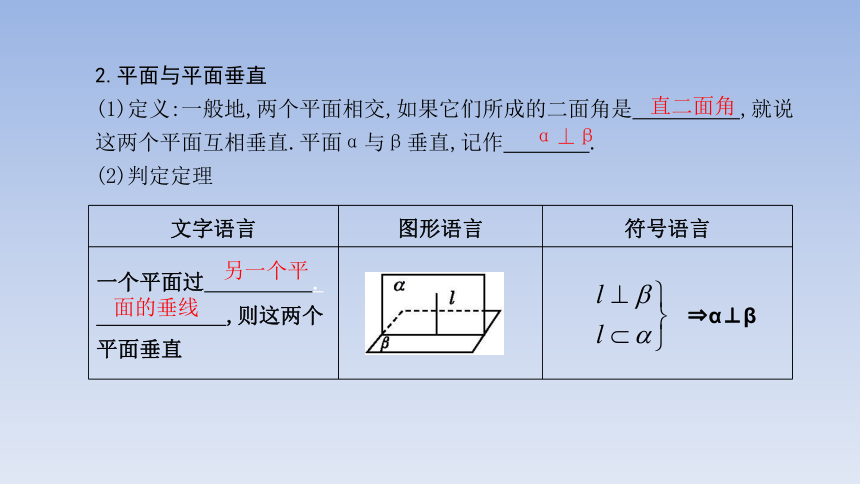
2.平面与平面垂直
(1)定义:一般地,两个平面相交,如果它们所成的二面角是 ,就说这两个平面互相垂直.平面α与β垂直,记作 .
(2)判定定理
直二面角
α⊥β
文字语言 图形语言 符号语言
一个平面过 . ,则这两个平面垂直 α⊥β
另一个平
面的垂线
探究:过平面外一点,可以作多少个与已知平面垂直的平面
答案:无数多个.过平面外一点可以作平面的一条垂线,过此垂线可以作出无数个平面,这些平面都与已知平面垂直.
1.下列结论:(1)两个相交平面组成的图形叫做二面角;
(2)异面直线a,b分别和一个二面角的两个半平面垂直,则a,b所成的角与这个二面角的平面角相等或互补.
(3)二面角的平面角是从棱上一点出发,分别在两个半平面内作射线所成角的最小角;
(4)二面角的大小与其平面角的顶点在棱上的位置没有关系.
其中正确的是( )
A.①③ B.②④
C.③④ D.①②
答案 B
小试牛刀
2.对于直线m,n和平面α,β,能得出α⊥β的一个条件是( )
A.m⊥n,m∥α,n∥β B.m⊥n,α∩β=m,n α
C.m∥n,n⊥β,m α D.m∥n,m⊥α,n⊥β
3.在正方体ABCD-A1B1C1D1的六个面中,与面ABCD垂直的平面有( )
A.1个 B.2个
C.3个 D.4个
答案 D
答案 C
4.如图,P是边长为2的正方形ABCD所在平面外一点,PA⊥AB,PA⊥ BC,且PC=5,则二面角P-BD-A的余弦值为 .
答案
题型分析 举一反三
(1)定义法:即说明两个平面所成的二面角是直二面角;
(2)判定定理法:其关键是在其中一个平面内寻找一直线与另一个平面垂直,即把问题转化为“线面垂直”;
(3)性质法:两个平行平面中的一个垂直于第三个平面,则另一个也垂直于此平面.
解题技巧(判定两平面垂直的常用方法)
1、如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M是棱CC1的中点.证明:平面ABM⊥平面A1B1M.
【跟踪训练1】
例2 如图所示,在正方体ABCD-A′B′C′D′中:
(1)求二面角D′-AB-D的大小;
(2)若M是C′D′的中点,求二面角M-AB-D的大小.
解析 (1)在正方体ABCD-A′B′C′D′中,AB⊥平面ADD′A′,所以AB⊥ AD′,AB⊥AD,因此∠D′AD为二面角D′-AB-D的平面角,
在Rt△D′DA中,∠D′AD=45°.
所以二面角D′-AB-D的大小为45°.
(2)因为M是C′D′的中点,所以MA=MB,取AB的中点N,连接MN,则MN⊥AB.取CD的中点H,连接HN,则HN⊥AB.
从而∠MNH是二面角M-AB-D的平面角.∠MNH=45°.
所以二面角M-AB-D的大小为45°.
(1)定义法:在二面角的棱上找一个特殊点,在两个半平面内分别作垂直于棱的射线.如图①,则∠AOB为二面角α-l-β的平面角.
解题技巧(作二面角的三种常用方法)
(2)垂直法:过棱上一点作棱的垂直平面,该平面与二面角的两个半平面产生交线,这两条交线所成的角,即为二面角的平面角.如图②,∠AOB为二面角α-l-β的平面角.
(3)垂线法:过二面角的一个面内异于棱上的一点A向另一个平面作垂线,垂足为B,由点B向二面角的棱作垂线,垂足为O,连接AO,则∠AOB为二面角的平面角或其补角.如图③,∠AOB为二面角α-l-β的平面角.
1、如图,在三棱锥P-ABC中,PA⊥平面PBC,PA=PB=2,PC=4,BC=2 .
(1)求证:平面PAB⊥平面ABC;
(2)E为BA的延长线上一点,若二面角P-EC-B的大小为30°,求BE的长.
【跟踪训练2】
(2)如图,取AB的中点F,连接PF.
因为PA=PB,所以PF⊥AB.由(1)知平面PAB⊥平面ABC,
又平面PAB∩平面ABC=AB,PF 平面PAB,
所以PF⊥平面ABC,PF⊥EC.
过F作FG⊥EC于G,连接PG.
因为PF⊥EC,PF∩FG=F,
所以EC⊥平面FPG.
因为PG 平面FPG,
所以EC⊥PG.
人教2019版必修第一册
第八章 立体几何初步
8.6.3 平面与平面垂直
第1课时 平面与平面垂直的判定
学习目标
1.理解二面角的概念,并会求简单的二面角;
2.理解直二面角与面面垂直的关系,理解平面和平面垂直的判定定理并能运用其解决相关问题.
3. 通过面面垂直定理的理解及运用,培养学生的空间转化能力和逻辑推理能力.
自主预习,回答问题
阅读课本155-158页,思考并完成以下问题
1、什么是二面角?什么是直二面角?
2、平面与平面平行的判定定理是什么?
3、怎样用符号语言表示平面与平面平行的判定定理?
要求:学生独立完成,以小组为单位,组内可商量,最终选出代表回答问题。
1.二面角
(1)定义:从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫二面角的 ,这两个半平面叫二面角的 .图中的二面角可记作:二面角α-AB-β或α-l-β或P-AB-Q.
棱
面
知识清单
(2)二面角的平面角:如图,在二面角α-l-β的棱l上任取一点O,以点O为垂足,在半平面α和β内分别作 的射线OA,OB,则射线OA和OB构成的∠AOB叫做二面角的平面角.平面角是 的二面角叫做直二面角.
垂直于棱l
直角
2.平面与平面垂直
(1)定义:一般地,两个平面相交,如果它们所成的二面角是 ,就说这两个平面互相垂直.平面α与β垂直,记作 .
(2)判定定理
直二面角
α⊥β
文字语言 图形语言 符号语言
一个平面过 . ,则这两个平面垂直 α⊥β
另一个平
面的垂线
探究:过平面外一点,可以作多少个与已知平面垂直的平面
答案:无数多个.过平面外一点可以作平面的一条垂线,过此垂线可以作出无数个平面,这些平面都与已知平面垂直.
1.下列结论:(1)两个相交平面组成的图形叫做二面角;
(2)异面直线a,b分别和一个二面角的两个半平面垂直,则a,b所成的角与这个二面角的平面角相等或互补.
(3)二面角的平面角是从棱上一点出发,分别在两个半平面内作射线所成角的最小角;
(4)二面角的大小与其平面角的顶点在棱上的位置没有关系.
其中正确的是( )
A.①③ B.②④
C.③④ D.①②
答案 B
小试牛刀
2.对于直线m,n和平面α,β,能得出α⊥β的一个条件是( )
A.m⊥n,m∥α,n∥β B.m⊥n,α∩β=m,n α
C.m∥n,n⊥β,m α D.m∥n,m⊥α,n⊥β
3.在正方体ABCD-A1B1C1D1的六个面中,与面ABCD垂直的平面有( )
A.1个 B.2个
C.3个 D.4个
答案 D
答案 C
4.如图,P是边长为2的正方形ABCD所在平面外一点,PA⊥AB,PA⊥ BC,且PC=5,则二面角P-BD-A的余弦值为 .
答案
题型分析 举一反三
(1)定义法:即说明两个平面所成的二面角是直二面角;
(2)判定定理法:其关键是在其中一个平面内寻找一直线与另一个平面垂直,即把问题转化为“线面垂直”;
(3)性质法:两个平行平面中的一个垂直于第三个平面,则另一个也垂直于此平面.
解题技巧(判定两平面垂直的常用方法)
1、如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M是棱CC1的中点.证明:平面ABM⊥平面A1B1M.
【跟踪训练1】
例2 如图所示,在正方体ABCD-A′B′C′D′中:
(1)求二面角D′-AB-D的大小;
(2)若M是C′D′的中点,求二面角M-AB-D的大小.
解析 (1)在正方体ABCD-A′B′C′D′中,AB⊥平面ADD′A′,所以AB⊥ AD′,AB⊥AD,因此∠D′AD为二面角D′-AB-D的平面角,
在Rt△D′DA中,∠D′AD=45°.
所以二面角D′-AB-D的大小为45°.
(2)因为M是C′D′的中点,所以MA=MB,取AB的中点N,连接MN,则MN⊥AB.取CD的中点H,连接HN,则HN⊥AB.
从而∠MNH是二面角M-AB-D的平面角.∠MNH=45°.
所以二面角M-AB-D的大小为45°.
(1)定义法:在二面角的棱上找一个特殊点,在两个半平面内分别作垂直于棱的射线.如图①,则∠AOB为二面角α-l-β的平面角.
解题技巧(作二面角的三种常用方法)
(2)垂直法:过棱上一点作棱的垂直平面,该平面与二面角的两个半平面产生交线,这两条交线所成的角,即为二面角的平面角.如图②,∠AOB为二面角α-l-β的平面角.
(3)垂线法:过二面角的一个面内异于棱上的一点A向另一个平面作垂线,垂足为B,由点B向二面角的棱作垂线,垂足为O,连接AO,则∠AOB为二面角的平面角或其补角.如图③,∠AOB为二面角α-l-β的平面角.
1、如图,在三棱锥P-ABC中,PA⊥平面PBC,PA=PB=2,PC=4,BC=2 .
(1)求证:平面PAB⊥平面ABC;
(2)E为BA的延长线上一点,若二面角P-EC-B的大小为30°,求BE的长.
【跟踪训练2】
(2)如图,取AB的中点F,连接PF.
因为PA=PB,所以PF⊥AB.由(1)知平面PAB⊥平面ABC,
又平面PAB∩平面ABC=AB,PF 平面PAB,
所以PF⊥平面ABC,PF⊥EC.
过F作FG⊥EC于G,连接PG.
因为PF⊥EC,PF∩FG=F,
所以EC⊥平面FPG.
因为PG 平面FPG,
所以EC⊥PG.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
