10.1.4 概率的基本性质(共57张PPT)
文档属性
| 名称 | 10.1.4 概率的基本性质(共57张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-24 00:00:00 | ||
图片预览











文档简介
(共57张PPT)
10.1.4 概率的基本性质
知识点 概率的基本性质
性质1 对任意的事件A,都有P(A) 0.
性质2 必然事件的概率为 ,不可能事件的概率为 ,即P(Ω)= ,P( )= .
性质3 如果事件A与事件B互斥,那么P(A∪B)= .
性质4 如果事件A与事件B互为对立事件,那么P(B)= ,P(A)= .
性质5 如果A B,那么 .
性质6 设A,B是一个随机试验中的两个事件,我们有P(A∪B)=_____
.
≥
1
0
1
0
P(A)+P(B)
1-P(A)
1-P(B)
P(A)≤P(B)
P(A)
+P(B)-P(A∩B)
例1 (1)抛掷一枚骰子,观察出现的点,设事件A为“出现1点”,B为“出现2点”.已知P(A)=P(B)= ,求出现1点或2点的概率.
一、互斥事件概率公式的应用
解 设事件C为“出现1点或2点”,因为事件A,B是互斥事件,
(2)盒子里装有6只红球,4只白球,从中任取3只球.设事件A表示“3只球中有1只红球,2只白球”,事件B表示“3只球中有2只红球,1只白球”.已知P(A)= ,P(B)= ,求这3只球中既有红球又有白球的概率.
解 因为A,B是互斥事件,
反思感悟
运用互斥事件的概率加法公式解题的一般步骤
(1)确定各事件彼此互斥.
(2)求各事件分别发生的概率,再求其和.
注意:(1)是公式使用的前提条件,不符合这点,是不能运用互斥事件的概率加法公式的.
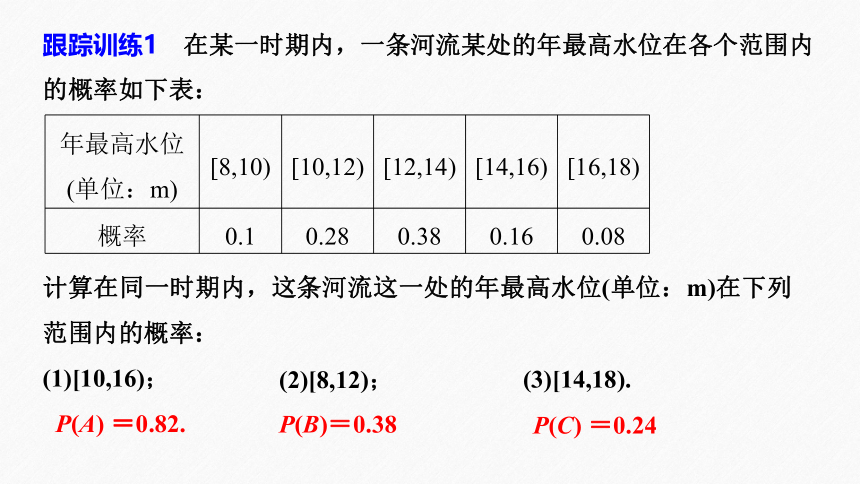
跟踪训练1 在某一时期内,一条河流某处的年最高水位在各个范围内的概率如下表:
年最高水位 (单位:m) [8,10) [10,12) [12,14) [14,16) [16,18)
概率 0.1 0.28 0.38 0.16 0.08
计算在同一时期内,这条河流这一处的年最高水位(单位:m)在下列范围内的概率:
(1)[10,16);
(2)[8,12);
(3)[14,18).
P(A) =0.82.
P(B)=0.38
P(C) =0.24
二、对立事件概率公式的应用
(1)甲获胜的概率;
解 “甲获胜”和“和棋或乙获胜”是对立事件,
(2)甲不输的概率.
(2)甲不输的概率.
解 方法一 设事件A为“甲不输”,可看成是“甲获胜”“和棋”这两个互斥事件的并事件,
方法二 设事件A为“甲不输”,可看成是“乙获胜”的对立事件,
反思感悟
对立事件也是比较重要的事件,利用对立事件的概率公式求解时,必须准确判断两个事件确实是对立事件时才能应用.
跟踪训练2 某战士射击一次,未中靶的概率为0.05,求中靶的概率.
中靶的概率是0.95.
三、概率性质的综合应用
(1)试分别求得到黑球、黄球、绿球的概率;
(2)从中任取一球,求得到的不是红球也不是绿球的概率.
解 从袋中任取一球,记事件“得到红球”“得到黑球”“得到黄球”
“得到绿球”分别为A,B,C,D,
(2)从中任取一球,求得到的不是红球也不是绿球的概率.
解 事件“得到红球或绿球”可表示为事件A∪D,
反思感悟
求某些较复杂事件的概率,通常有两种方法:
一是将所求事件的概率转化成一些彼此互斥的事件的概率的和;
二是先求此事件的对立事件的概率,再用公式求此事件的概率.这两种方法可使复杂事件概率的计算得到简化.
跟踪训练3 某公务员去开会,他乘火车、轮船、汽车、飞机去的概率分别为0.3,0.2,0.1,0.4.
(1)求他乘火车或乘飞机去的概率;
解 记“他乘火车”为事件A,“他乘轮船”为事件B,“他乘汽车”为事件C,“他乘飞机”为事件D.
这四个事件两两不可能同时发生,故它们彼此互斥,所以P(A∪D)=P(A)+P(D)=0.3+0.4=0.7.
即他乘火车或乘飞机去的概率为0.7.
(2)求他不乘轮船去的概率;
(2)求他不乘轮船去的概率;
解 设他不乘轮船去的概率为P,则P=1-P(B)=1-0.2=0.8,
所以他不乘轮船去的概率为0.8.
(3)如果他乘交通工具的概率为0.5,请问他有可能乘哪种交通工具?
解 由于P(A)+P(B)=0.3+0.2=0.5,
P(C)+P(D)=0.1+0.4=0.5,
故他可能乘火车或乘轮船去,也有可能乘汽车或乘飞机去.
核心素养之逻辑推理
HE XIN SU YANG ZHI LUO JI TUI LI
正难则反思想的应用
典例 一个盒子里装有三张卡片,分别标记有数字1,2,3,这三张卡片除标记的数字外完全相同.随机有放回地抽取3次,每次抽取1张,将抽取的卡片上的数字依次记为a,b,c.
(1)求“抽取的卡片上的数字满足a+b=c”的概率;
(2)求“抽取的卡片上的数字a,b,c不完全相同”的概率.
解 由题意知,(a,b,c)的样本空间Ω={(1,1,1),(1,1,2),(1,1,3),(1,2,1),(1,2,2),(1,2,3),(1,3,1),(1,3,2),(1,3,3),(2,1,1),(2,1,2),(2,1,3),(2,2,1),(2,2,2),(2,2,3),(2,3,1),(2,3,2),(2,3,3),(3,1,1),(3,1,2),(3,1,3),(3,2,1),(3,2,2),(3,2,3),(3,3,1),(3,3,2),(3,3,3)},共27个样本点.
设“抽取的卡片上的数字满足a+b=c”为事件A,
则事件A包含的样本点有(1,1,2),(1,2,3),(2,1,3),共3个.
(2)求“抽取的卡片上的数字a,b,c不完全相同”的概率.
解 设“抽取的卡片上的数字a,b,c不完全相同”为事件B,
素养提升
当正面考虑所解决的问题比较烦琐复杂时,可以找到所求事件的对立事件,利用对立事件的概率的公式求解.正难则反思想的应用提高了逻辑推理的核心素养.
3
随堂演练
PART THREE
1
2
3
4
5
1.在一个试验中,若P(A+B)=P(A)+P(B)=1,事件A与事件B的关系是
A.互斥不对立 B.对立不互斥
C.互斥且对立 D.以上答案都不对
√
1
2
3
4
5
2.口袋内装有一些大小相同的红球、白球和黑球,从中摸出1个球,摸出红球的概率是0.42,摸出白球的概率是0.28,那么摸出黑球的概率是
A.0.42 B.0.28 C.0.3 D.0.7
√
解析 ∵摸出黑球是摸出红球或摸出白球的对立事件,
∴摸出黑球的概率是1-0.42-0.28=0.3,故选C.
3.事件A与事件B的关系如图所示,则
A.A B B.A B
C.A与B互斥 D.A与B互为对立事件
√
1
2
3
4
5
解析 由题图知,事件A与事件B不能同时发生,且A∪B≠Ω,
因此A与B互斥不对立,故选C.
4.袋中有形状、大小都相同的4只球,其中1只白球,1只红球,2只黄球.
从中一次随机摸出2只球,则这2只球颜色不同的概率为_____.
1
2
3
4
5
1
2
3
4
5
5.已知射手甲射击一次,命中9环以上(含9环)的概率为0.5,命中8环的概率为0.2,命中7环的概率为0.1,则甲射击一次,命中6环以下(含6环)的概率为______.
0.2
解析 设“命中9环以上(含9环)”为事件A,“命中8环”为事件B,“命中7环”为事件C,“命中6环以下(含6环)”为事件D,
则D与A∪B∪C互为对立事件.
因为P(A)=0.5,P(B)=0.2,P(C)=0.1,且A,B,C三个事件互斥,
所以P(A∪B∪C)=P(A)+P(B)+P(C)=0.8,所以P(D)=1-0.8=0.2.
课堂小结
KE TANG XIAO JIE
1.知识清单:
性质1 对任意的事件A,都有P(A)≥0.
性质2 必然事件的概率为1,不可能事件的概率为0,即P(Ω)=1,P( )=0.
性质3 如果事件A与事件B互斥,那么P(A∪B)=P(A)+P(B).
性质4 如果事件A与事件B互为对立事件,那么P(B)=1-P(A),P(A)=1-P(B).
性质5 如果A B,那么P(A)≤P(B).
性质6 设A,B是一个随机试验中的两个事件,我们有P(A∪B)=P(A)+P(B)-P(A∩B).
2.方法归纳:转化法、正难则反.
3.常见误区:将事件拆分成若干个互斥的事件,易重复和遗漏.
4
课时对点练
PART FOUR
基础巩固
1.P(A)=0.1,P(B)=0.2,则P(A+B)等于
A.0.3 B.0.2
C.0.1 D.不能确定
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由于不能确定A与B是否互斥,则P(A+B)的值不能确定.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.在一次随机试验中,彼此互斥的事件A,B,C,D的概率分别是0.2,
0.2,0.3,0.3,则下列说法正确的是
A.A+B与C是互斥事件,也是对立事件
B.B+C与D是互斥事件,也是对立事件
C.A+C与B+D是互斥事件,但不是对立事件
D.A与B+C+D是互斥事件,也是对立事件
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由于A,B,C,D彼此互斥,且由P(A+B+C
+D)=P(A)+P(B)+P(C)+P(D)=1,知A+B+C+D是一个必然事件,故其事件的关系如图所示.
由图可知,任何一个事件与其余3个事件的和事件必然是对立事件,任何两个事件的和事件与其余两个事件的和事件也是对立事件,故只有D中的说法正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.若事件A和B是互斥事件,且P(A)=0.1,则P(B)的取值范围是
A.[0,0.9] B.[0.1,0.9]
C.(0,0.9] D.[0,1]
√
解析 由于事件A和B是互斥事件,
则P(A+B)=P(A)+P(B)=0.1+P(B),
又0≤P(A+B)≤1,所以0≤0.1+P(B)≤1,
又P(B)≥0,所以0≤P(B)≤0.9,故选A.
4.从一箱产品中随机地抽取一件,设事件A=“抽到一等品”,事件B=“抽到二等品”,事件C=“抽到三等品”.已知P(A)=0.65,P(B)=0.2,P(C)=0.1,则事件“抽到的不是一等品”的概率为
A.0.20 B.0.39
C.0.35 D.0.30
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 ∵抽到的不是一等品的对立事件是抽到一等品,而P(A)=0.65,
∴抽到的不是一等品的概率是1-0.65=0.35.
5.从一批羽毛球产品中任取一个,其质量小于4.8 g的概率为0.3,质量小于4.85 g的概率为0.32,那么质量在4.8~4.85 g范围内的概率是
A.0.62 B.0.38
C.0.02 D.0.68
√
解析 设“质量小于4.8 g”为事件A,“质量小于4.85 g”为事件B,“质量在4.8~4.85 g”为事件C,
则A+C=B,且A,C为互斥事件,所以P(B)=P(A+C)=P(A)+P(C),
则P(C)=P(B)-P(A)=0.32-0.3=0.02.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.某城市2019年的空气质量状况如下表所示:
其中污染指数T≤50时,空气质量为优;50或优的概率为_____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由于空气质量达到良或优为污染指数T≤100,
由互斥事件概率的加法公式,
7.事件A,B互斥,它们都不发生的概率为 ,且P(A)=2P(B),则P(A)
=_____.
又因为P(A)=2P(B),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.某饮料公司对一名员工进行测试以便确定其考评级别.公司准备了两种不同的饮料共5杯,其颜色完全相同,并且其中3杯为A饮料,另外2杯为B饮料,公司要求此员工一一品尝后,从5杯饮料中选出3杯A饮料.若该员工3杯都选对,则评为优秀;若3杯选对2杯,则评为良好;否则评为不合格.假设此人对A和B两种饮料没有鉴别能力.
(1)求此人被评为优秀的概率;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 将5杯饮料编号为1,2,3,4,5,编号1,2,3表示A饮料,编号4,5表示B饮料,
则从5杯饮料中选出3杯的样本空间Ω={(123),(124),(125),(134),(135),(145),(234),(235),(245),(345)},共有10个样本点.
令D表示此人被评为优秀的事件,E表示此人被评为良好的事件,F表示此人被评为良好及以上的事件,则
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求此人被评为良好及以上的概率.
10.袋中有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分别为4,5.从这五张卡片中任取两张,如果5张卡片被抽取的机会相等,分别计算下列事件的概率:
(1)事件A=“这两张卡片颜色不同”;
解 从五张卡片中任取两张,对应的样本空间Ω={(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)},共有10个样本点.
A={(1,4),(1,5),(2,4),(2,5),(3,4),(3,5)},共有6个样本点,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)事件B=“这两张卡片标号之和小于7”;
解 B={(1,2),(1,3),(1,4),(1,5),(2,3),(2,4)},共有6个样本点,
(3)事件C=“这两张卡片颜色不同且标号之和小于7”.
解 C={(1,4),(1,5),(2,4)},共有3个样本点,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(4)事件D=“这两张卡片标号之和不小于7”.
解 由题意得,事件D与事件B是对立事件,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
11.已知a∈{0,1,2},b∈{-1,1,3,5},则函数f(x)=ax2-2bx在区间(1,+∞)上为增函数的概率是
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 ∵a∈{0,1,2},b∈{-1,1,3,5},
∴共含有12个样本点.
函数f(x)=ax2-2bx在区间(1,+∞)上为增函数,
①当a=0时,f(x)=-2bx,符合条件的只有(0,-1),即a=0,b=-1;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.在5件产品中,有3件一级品和2件二级品,从中任取2件,下列事件中概率为 的是
A.都是一级品 B.都是二级品
C.一级品和二级品各1件 D.至少有1件二级品
√
解析 样本点总数为10,2件都是一级品包含的样本点有3个,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.(多选)黄种人群中各种血型的人所占的比例见右表:
血型 A B AB O
该血型的人所占比例 0.28 0.29 0.08 0.35
已知同种血型的人可以输血,O型血可以给任何一种血型的人输血,任何血型的人都可以给AB血型的人输血,其他不同血型的人不能互相输血.下列结论正确的是
A.任找一个人,其血可以输给B型血的人的概率是0.64
B.任找一个人,B型血的人能为其输血的概率是0.29
C.任找一个人,其血可以输给O型血的人的概率为1
D.任找一个人,其血可以输给AB型血的人的概率为1
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 任找一个人,其血型为A,B,AB,O型血的事件分别为A′,B′,C′,D′,它们两两互斥.
由已知,有P(A′)=0.28,P(B′)=0.29,P(C′)=0.08,P(D′)=0.35.
因为B,O型血可以输给B型血的人,所以“可以输给B型血的人”为事件B′∪D′,根据概率的加法公式,得P(B′∪D′)=P(B′)+P(D′)=0.29+0.35=0.64,故A正确;
B型血的人能为B型、AB型的人输血,其概率为0.29+0.08=0.37,B错误;
由O型血只能接受O型血的人输血知,C错误;
由任何人的血都可以输给AB型血的人,知D正确.故选A,D.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.在一次教师联欢会上,到会的女教师比男教师多12人,从这些教师中随机挑选一人表演节目,若选中男教师的概率为 ,则参加联欢会的教师共有______人.
120
解析 可设参加联欢会的教师共有n人,由于从这些教师中选一人,“选中男教师”和“选中女教师”两个事件是对立事件,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15.甲、乙两人从1,2,3,…,10中各任取一数(不重复),已知甲取到的
数是5的倍数,则甲数大于乙数的概率为_____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 甲、乙两人从1,2,3,…,10中各任取一数(不重复),甲取到的数是5的倍数,设甲取的数为m,乙取的数为n,其样本点记为(m,n),
所以样本空间Ω={(5,1),(5,2),(5,3),(5,4),(5,6),(5,7),(5,8),(5,9),(5,10),(10,1),(10,2),(10,3),(10,4),(10,5),(10,6),(10,7),(10,8),(10,9)},共含有18个样本点,事件“甲数小于乙数”包括(5,6),(5,7),(5,8),(5,9),(5,10),共5个样本点,
16.某商场有奖销售中,购物满100元可得1张奖券,多购多得.1 000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖50个.设1张奖券中特等奖、一等奖、二等奖的事件分别为A,B,C,求:
(1)P(A),P(B),P(C);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)1张奖券的中奖概率;
解 1张奖券中奖包含中特等奖,一等奖,二等奖.
设“1张奖券中奖”这个事件为M,则M=A∪B∪C.
∵A,B,C两两互斥,
∴P(M)=P(A∪B∪C)=P(A)+P(B)+P(C)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(3)1张奖券不中特等奖且不中一等奖的概率.
解 设“1张奖券不中特等奖且不中一等奖”为事件N,
则事件N与“1张奖券中特等奖或中一等奖”互为对立事件,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
本课结束
10.1.4 概率的基本性质
知识点 概率的基本性质
性质1 对任意的事件A,都有P(A) 0.
性质2 必然事件的概率为 ,不可能事件的概率为 ,即P(Ω)= ,P( )= .
性质3 如果事件A与事件B互斥,那么P(A∪B)= .
性质4 如果事件A与事件B互为对立事件,那么P(B)= ,P(A)= .
性质5 如果A B,那么 .
性质6 设A,B是一个随机试验中的两个事件,我们有P(A∪B)=_____
.
≥
1
0
1
0
P(A)+P(B)
1-P(A)
1-P(B)
P(A)≤P(B)
P(A)
+P(B)-P(A∩B)
例1 (1)抛掷一枚骰子,观察出现的点,设事件A为“出现1点”,B为“出现2点”.已知P(A)=P(B)= ,求出现1点或2点的概率.
一、互斥事件概率公式的应用
解 设事件C为“出现1点或2点”,因为事件A,B是互斥事件,
(2)盒子里装有6只红球,4只白球,从中任取3只球.设事件A表示“3只球中有1只红球,2只白球”,事件B表示“3只球中有2只红球,1只白球”.已知P(A)= ,P(B)= ,求这3只球中既有红球又有白球的概率.
解 因为A,B是互斥事件,
反思感悟
运用互斥事件的概率加法公式解题的一般步骤
(1)确定各事件彼此互斥.
(2)求各事件分别发生的概率,再求其和.
注意:(1)是公式使用的前提条件,不符合这点,是不能运用互斥事件的概率加法公式的.
跟踪训练1 在某一时期内,一条河流某处的年最高水位在各个范围内的概率如下表:
年最高水位 (单位:m) [8,10) [10,12) [12,14) [14,16) [16,18)
概率 0.1 0.28 0.38 0.16 0.08
计算在同一时期内,这条河流这一处的年最高水位(单位:m)在下列范围内的概率:
(1)[10,16);
(2)[8,12);
(3)[14,18).
P(A) =0.82.
P(B)=0.38
P(C) =0.24
二、对立事件概率公式的应用
(1)甲获胜的概率;
解 “甲获胜”和“和棋或乙获胜”是对立事件,
(2)甲不输的概率.
(2)甲不输的概率.
解 方法一 设事件A为“甲不输”,可看成是“甲获胜”“和棋”这两个互斥事件的并事件,
方法二 设事件A为“甲不输”,可看成是“乙获胜”的对立事件,
反思感悟
对立事件也是比较重要的事件,利用对立事件的概率公式求解时,必须准确判断两个事件确实是对立事件时才能应用.
跟踪训练2 某战士射击一次,未中靶的概率为0.05,求中靶的概率.
中靶的概率是0.95.
三、概率性质的综合应用
(1)试分别求得到黑球、黄球、绿球的概率;
(2)从中任取一球,求得到的不是红球也不是绿球的概率.
解 从袋中任取一球,记事件“得到红球”“得到黑球”“得到黄球”
“得到绿球”分别为A,B,C,D,
(2)从中任取一球,求得到的不是红球也不是绿球的概率.
解 事件“得到红球或绿球”可表示为事件A∪D,
反思感悟
求某些较复杂事件的概率,通常有两种方法:
一是将所求事件的概率转化成一些彼此互斥的事件的概率的和;
二是先求此事件的对立事件的概率,再用公式求此事件的概率.这两种方法可使复杂事件概率的计算得到简化.
跟踪训练3 某公务员去开会,他乘火车、轮船、汽车、飞机去的概率分别为0.3,0.2,0.1,0.4.
(1)求他乘火车或乘飞机去的概率;
解 记“他乘火车”为事件A,“他乘轮船”为事件B,“他乘汽车”为事件C,“他乘飞机”为事件D.
这四个事件两两不可能同时发生,故它们彼此互斥,所以P(A∪D)=P(A)+P(D)=0.3+0.4=0.7.
即他乘火车或乘飞机去的概率为0.7.
(2)求他不乘轮船去的概率;
(2)求他不乘轮船去的概率;
解 设他不乘轮船去的概率为P,则P=1-P(B)=1-0.2=0.8,
所以他不乘轮船去的概率为0.8.
(3)如果他乘交通工具的概率为0.5,请问他有可能乘哪种交通工具?
解 由于P(A)+P(B)=0.3+0.2=0.5,
P(C)+P(D)=0.1+0.4=0.5,
故他可能乘火车或乘轮船去,也有可能乘汽车或乘飞机去.
核心素养之逻辑推理
HE XIN SU YANG ZHI LUO JI TUI LI
正难则反思想的应用
典例 一个盒子里装有三张卡片,分别标记有数字1,2,3,这三张卡片除标记的数字外完全相同.随机有放回地抽取3次,每次抽取1张,将抽取的卡片上的数字依次记为a,b,c.
(1)求“抽取的卡片上的数字满足a+b=c”的概率;
(2)求“抽取的卡片上的数字a,b,c不完全相同”的概率.
解 由题意知,(a,b,c)的样本空间Ω={(1,1,1),(1,1,2),(1,1,3),(1,2,1),(1,2,2),(1,2,3),(1,3,1),(1,3,2),(1,3,3),(2,1,1),(2,1,2),(2,1,3),(2,2,1),(2,2,2),(2,2,3),(2,3,1),(2,3,2),(2,3,3),(3,1,1),(3,1,2),(3,1,3),(3,2,1),(3,2,2),(3,2,3),(3,3,1),(3,3,2),(3,3,3)},共27个样本点.
设“抽取的卡片上的数字满足a+b=c”为事件A,
则事件A包含的样本点有(1,1,2),(1,2,3),(2,1,3),共3个.
(2)求“抽取的卡片上的数字a,b,c不完全相同”的概率.
解 设“抽取的卡片上的数字a,b,c不完全相同”为事件B,
素养提升
当正面考虑所解决的问题比较烦琐复杂时,可以找到所求事件的对立事件,利用对立事件的概率的公式求解.正难则反思想的应用提高了逻辑推理的核心素养.
3
随堂演练
PART THREE
1
2
3
4
5
1.在一个试验中,若P(A+B)=P(A)+P(B)=1,事件A与事件B的关系是
A.互斥不对立 B.对立不互斥
C.互斥且对立 D.以上答案都不对
√
1
2
3
4
5
2.口袋内装有一些大小相同的红球、白球和黑球,从中摸出1个球,摸出红球的概率是0.42,摸出白球的概率是0.28,那么摸出黑球的概率是
A.0.42 B.0.28 C.0.3 D.0.7
√
解析 ∵摸出黑球是摸出红球或摸出白球的对立事件,
∴摸出黑球的概率是1-0.42-0.28=0.3,故选C.
3.事件A与事件B的关系如图所示,则
A.A B B.A B
C.A与B互斥 D.A与B互为对立事件
√
1
2
3
4
5
解析 由题图知,事件A与事件B不能同时发生,且A∪B≠Ω,
因此A与B互斥不对立,故选C.
4.袋中有形状、大小都相同的4只球,其中1只白球,1只红球,2只黄球.
从中一次随机摸出2只球,则这2只球颜色不同的概率为_____.
1
2
3
4
5
1
2
3
4
5
5.已知射手甲射击一次,命中9环以上(含9环)的概率为0.5,命中8环的概率为0.2,命中7环的概率为0.1,则甲射击一次,命中6环以下(含6环)的概率为______.
0.2
解析 设“命中9环以上(含9环)”为事件A,“命中8环”为事件B,“命中7环”为事件C,“命中6环以下(含6环)”为事件D,
则D与A∪B∪C互为对立事件.
因为P(A)=0.5,P(B)=0.2,P(C)=0.1,且A,B,C三个事件互斥,
所以P(A∪B∪C)=P(A)+P(B)+P(C)=0.8,所以P(D)=1-0.8=0.2.
课堂小结
KE TANG XIAO JIE
1.知识清单:
性质1 对任意的事件A,都有P(A)≥0.
性质2 必然事件的概率为1,不可能事件的概率为0,即P(Ω)=1,P( )=0.
性质3 如果事件A与事件B互斥,那么P(A∪B)=P(A)+P(B).
性质4 如果事件A与事件B互为对立事件,那么P(B)=1-P(A),P(A)=1-P(B).
性质5 如果A B,那么P(A)≤P(B).
性质6 设A,B是一个随机试验中的两个事件,我们有P(A∪B)=P(A)+P(B)-P(A∩B).
2.方法归纳:转化法、正难则反.
3.常见误区:将事件拆分成若干个互斥的事件,易重复和遗漏.
4
课时对点练
PART FOUR
基础巩固
1.P(A)=0.1,P(B)=0.2,则P(A+B)等于
A.0.3 B.0.2
C.0.1 D.不能确定
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由于不能确定A与B是否互斥,则P(A+B)的值不能确定.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.在一次随机试验中,彼此互斥的事件A,B,C,D的概率分别是0.2,
0.2,0.3,0.3,则下列说法正确的是
A.A+B与C是互斥事件,也是对立事件
B.B+C与D是互斥事件,也是对立事件
C.A+C与B+D是互斥事件,但不是对立事件
D.A与B+C+D是互斥事件,也是对立事件
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由于A,B,C,D彼此互斥,且由P(A+B+C
+D)=P(A)+P(B)+P(C)+P(D)=1,知A+B+C+D是一个必然事件,故其事件的关系如图所示.
由图可知,任何一个事件与其余3个事件的和事件必然是对立事件,任何两个事件的和事件与其余两个事件的和事件也是对立事件,故只有D中的说法正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.若事件A和B是互斥事件,且P(A)=0.1,则P(B)的取值范围是
A.[0,0.9] B.[0.1,0.9]
C.(0,0.9] D.[0,1]
√
解析 由于事件A和B是互斥事件,
则P(A+B)=P(A)+P(B)=0.1+P(B),
又0≤P(A+B)≤1,所以0≤0.1+P(B)≤1,
又P(B)≥0,所以0≤P(B)≤0.9,故选A.
4.从一箱产品中随机地抽取一件,设事件A=“抽到一等品”,事件B=“抽到二等品”,事件C=“抽到三等品”.已知P(A)=0.65,P(B)=0.2,P(C)=0.1,则事件“抽到的不是一等品”的概率为
A.0.20 B.0.39
C.0.35 D.0.30
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 ∵抽到的不是一等品的对立事件是抽到一等品,而P(A)=0.65,
∴抽到的不是一等品的概率是1-0.65=0.35.
5.从一批羽毛球产品中任取一个,其质量小于4.8 g的概率为0.3,质量小于4.85 g的概率为0.32,那么质量在4.8~4.85 g范围内的概率是
A.0.62 B.0.38
C.0.02 D.0.68
√
解析 设“质量小于4.8 g”为事件A,“质量小于4.85 g”为事件B,“质量在4.8~4.85 g”为事件C,
则A+C=B,且A,C为互斥事件,所以P(B)=P(A+C)=P(A)+P(C),
则P(C)=P(B)-P(A)=0.32-0.3=0.02.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.某城市2019年的空气质量状况如下表所示:
其中污染指数T≤50时,空气质量为优;50
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由于空气质量达到良或优为污染指数T≤100,
由互斥事件概率的加法公式,
7.事件A,B互斥,它们都不发生的概率为 ,且P(A)=2P(B),则P(A)
=_____.
又因为P(A)=2P(B),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.某饮料公司对一名员工进行测试以便确定其考评级别.公司准备了两种不同的饮料共5杯,其颜色完全相同,并且其中3杯为A饮料,另外2杯为B饮料,公司要求此员工一一品尝后,从5杯饮料中选出3杯A饮料.若该员工3杯都选对,则评为优秀;若3杯选对2杯,则评为良好;否则评为不合格.假设此人对A和B两种饮料没有鉴别能力.
(1)求此人被评为优秀的概率;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 将5杯饮料编号为1,2,3,4,5,编号1,2,3表示A饮料,编号4,5表示B饮料,
则从5杯饮料中选出3杯的样本空间Ω={(123),(124),(125),(134),(135),(145),(234),(235),(245),(345)},共有10个样本点.
令D表示此人被评为优秀的事件,E表示此人被评为良好的事件,F表示此人被评为良好及以上的事件,则
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求此人被评为良好及以上的概率.
10.袋中有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分别为4,5.从这五张卡片中任取两张,如果5张卡片被抽取的机会相等,分别计算下列事件的概率:
(1)事件A=“这两张卡片颜色不同”;
解 从五张卡片中任取两张,对应的样本空间Ω={(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)},共有10个样本点.
A={(1,4),(1,5),(2,4),(2,5),(3,4),(3,5)},共有6个样本点,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)事件B=“这两张卡片标号之和小于7”;
解 B={(1,2),(1,3),(1,4),(1,5),(2,3),(2,4)},共有6个样本点,
(3)事件C=“这两张卡片颜色不同且标号之和小于7”.
解 C={(1,4),(1,5),(2,4)},共有3个样本点,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(4)事件D=“这两张卡片标号之和不小于7”.
解 由题意得,事件D与事件B是对立事件,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
11.已知a∈{0,1,2},b∈{-1,1,3,5},则函数f(x)=ax2-2bx在区间(1,+∞)上为增函数的概率是
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 ∵a∈{0,1,2},b∈{-1,1,3,5},
∴共含有12个样本点.
函数f(x)=ax2-2bx在区间(1,+∞)上为增函数,
①当a=0时,f(x)=-2bx,符合条件的只有(0,-1),即a=0,b=-1;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.在5件产品中,有3件一级品和2件二级品,从中任取2件,下列事件中概率为 的是
A.都是一级品 B.都是二级品
C.一级品和二级品各1件 D.至少有1件二级品
√
解析 样本点总数为10,2件都是一级品包含的样本点有3个,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.(多选)黄种人群中各种血型的人所占的比例见右表:
血型 A B AB O
该血型的人所占比例 0.28 0.29 0.08 0.35
已知同种血型的人可以输血,O型血可以给任何一种血型的人输血,任何血型的人都可以给AB血型的人输血,其他不同血型的人不能互相输血.下列结论正确的是
A.任找一个人,其血可以输给B型血的人的概率是0.64
B.任找一个人,B型血的人能为其输血的概率是0.29
C.任找一个人,其血可以输给O型血的人的概率为1
D.任找一个人,其血可以输给AB型血的人的概率为1
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 任找一个人,其血型为A,B,AB,O型血的事件分别为A′,B′,C′,D′,它们两两互斥.
由已知,有P(A′)=0.28,P(B′)=0.29,P(C′)=0.08,P(D′)=0.35.
因为B,O型血可以输给B型血的人,所以“可以输给B型血的人”为事件B′∪D′,根据概率的加法公式,得P(B′∪D′)=P(B′)+P(D′)=0.29+0.35=0.64,故A正确;
B型血的人能为B型、AB型的人输血,其概率为0.29+0.08=0.37,B错误;
由O型血只能接受O型血的人输血知,C错误;
由任何人的血都可以输给AB型血的人,知D正确.故选A,D.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.在一次教师联欢会上,到会的女教师比男教师多12人,从这些教师中随机挑选一人表演节目,若选中男教师的概率为 ,则参加联欢会的教师共有______人.
120
解析 可设参加联欢会的教师共有n人,由于从这些教师中选一人,“选中男教师”和“选中女教师”两个事件是对立事件,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15.甲、乙两人从1,2,3,…,10中各任取一数(不重复),已知甲取到的
数是5的倍数,则甲数大于乙数的概率为_____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 甲、乙两人从1,2,3,…,10中各任取一数(不重复),甲取到的数是5的倍数,设甲取的数为m,乙取的数为n,其样本点记为(m,n),
所以样本空间Ω={(5,1),(5,2),(5,3),(5,4),(5,6),(5,7),(5,8),(5,9),(5,10),(10,1),(10,2),(10,3),(10,4),(10,5),(10,6),(10,7),(10,8),(10,9)},共含有18个样本点,事件“甲数小于乙数”包括(5,6),(5,7),(5,8),(5,9),(5,10),共5个样本点,
16.某商场有奖销售中,购物满100元可得1张奖券,多购多得.1 000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖50个.设1张奖券中特等奖、一等奖、二等奖的事件分别为A,B,C,求:
(1)P(A),P(B),P(C);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)1张奖券的中奖概率;
解 1张奖券中奖包含中特等奖,一等奖,二等奖.
设“1张奖券中奖”这个事件为M,则M=A∪B∪C.
∵A,B,C两两互斥,
∴P(M)=P(A∪B∪C)=P(A)+P(B)+P(C)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(3)1张奖券不中特等奖且不中一等奖的概率.
解 设“1张奖券不中特等奖且不中一等奖”为事件N,
则事件N与“1张奖券中特等奖或中一等奖”互为对立事件,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
本课结束
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
