倾斜角与斜率
图片预览






文档简介
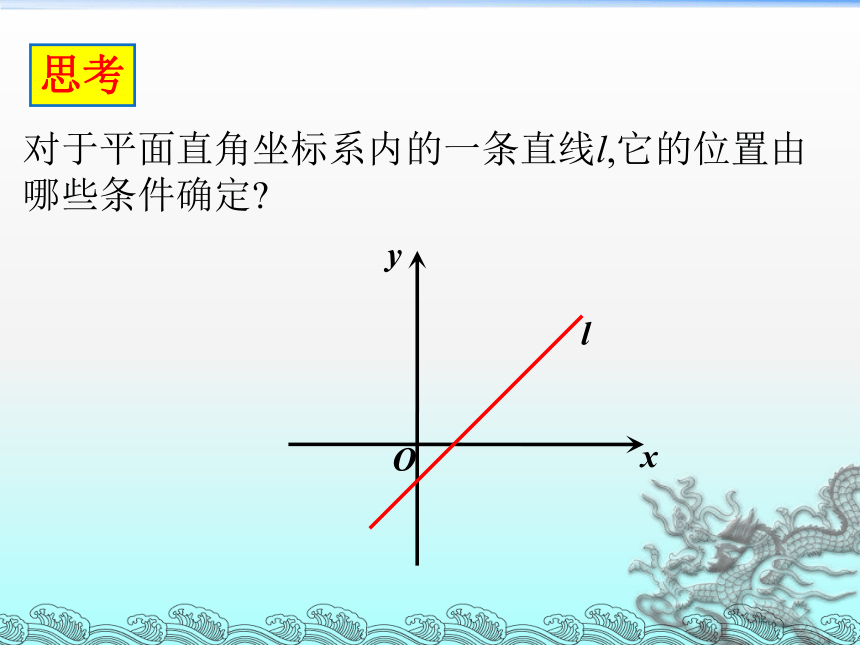
课件47张PPT。3.1.1倾斜角与斜率对于平面直角坐标系内的一条直线l,它的位置由哪些条件确定?思考 我们知道,两点确定一条直线.
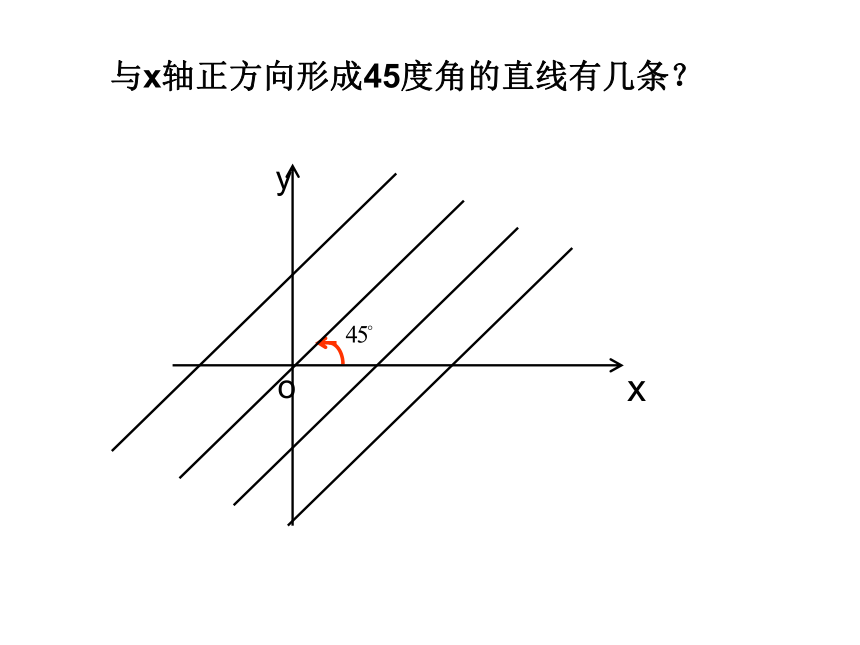
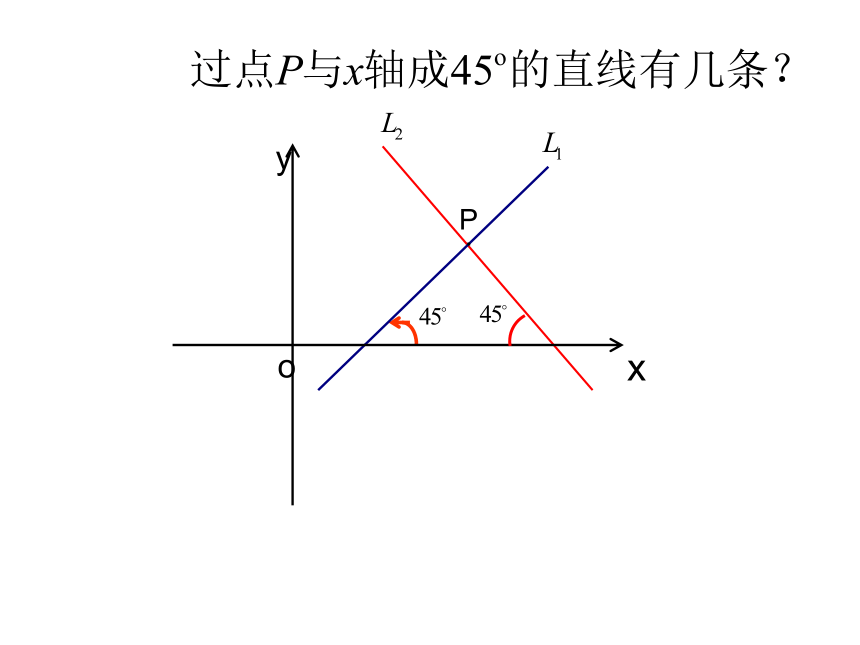
一点能确定一条直线的位置吗?已知直线l 经过点P,直线l 的位置能够确定吗?过一点有无数条直线,故一点不能确定直线。P 与x轴正方向形成45度角的直线有几条? P.
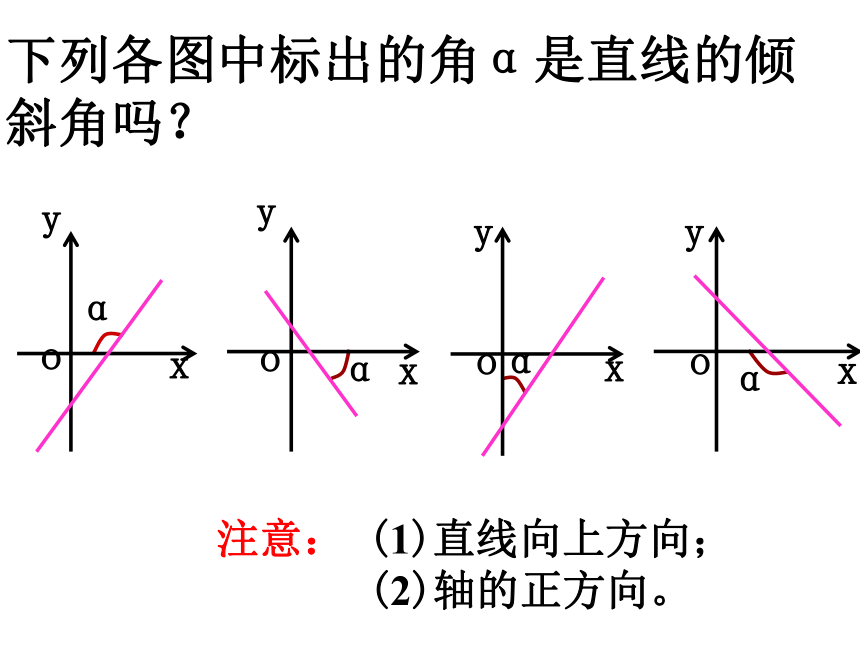
在平面直角坐标系中,确定一条直线位置的条件是:已知直线上的一个点和这条直线的方向。而直线的方向我们就是用倾斜角来刻画的。 当直线 l 与x轴相交时,我们取x轴作为基准,x轴正向与直线 l 向上方向之间所成的角α 叫做直线 l 的倾斜角(angle of inclination) .xyOl 当直线l与x轴平行或重合时,规定它的倾斜角为 .直线的倾斜角 的取值范围为:直线的倾斜角P.我们把 和 角就叫做直线 与 的倾斜角。下列各图中标出的角α是直线的倾斜角吗? oα注意: (1)直线向上方向;
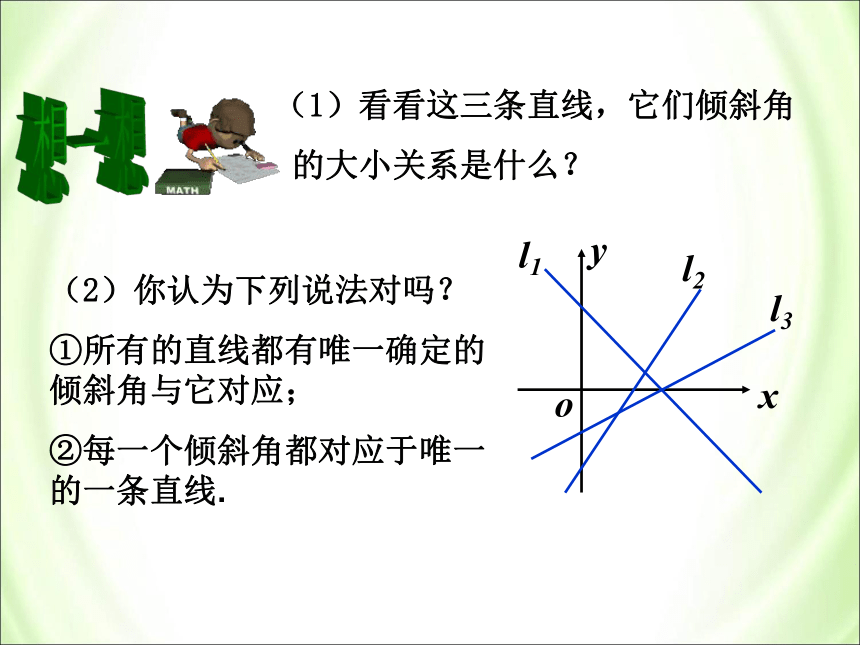
(2)轴的正方向。(1)看看这三条直线,它们倾斜角
的大小关系是什么?l1l2l3(2)你认为下列说法对吗?
①所有的直线都有唯一确定的倾斜角与它对应;
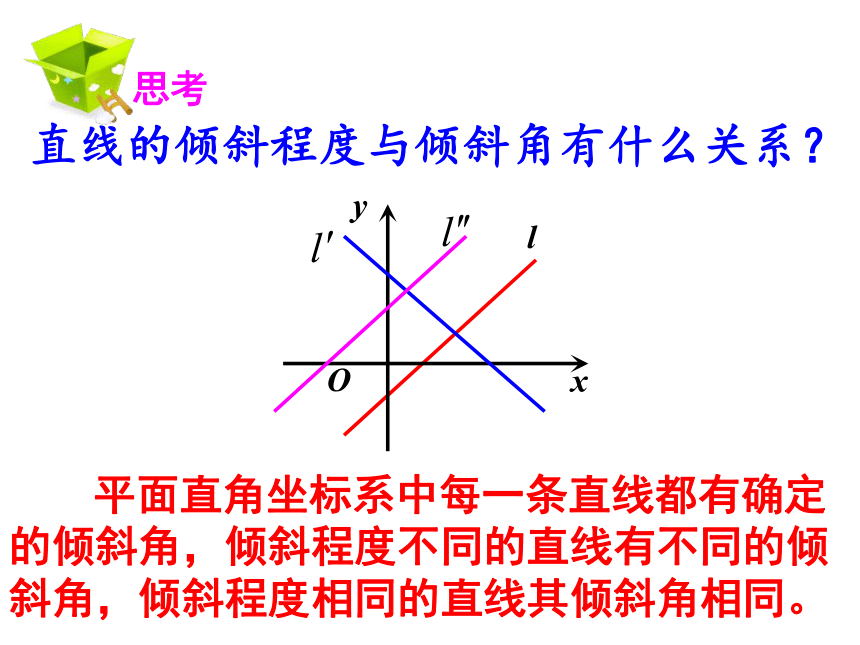
②每一个倾斜角都对应于唯一的一条直线.直线的倾斜程度与倾斜角有什么关系? 平面直角坐标系中每一条直线都有确定的倾斜角,倾斜程度不同的直线有不同的倾斜角,倾斜程度相同的直线其倾斜角相同。 思考 只知道直线的倾斜角α,不能确定一条直线的位置。 已知直线上的一个点不能确定一条直线的位置,那已知直线的倾斜角α,能不能确定一条直线的位置? 确定平面直角坐标系中一条直线位置的几何要素是:
直线上的一个定点以及它的倾斜角, 二者缺一不可.确定直线的要素 日常生活中,还有没有表示
倾斜程度的量?(即倾斜角a的正切值) 一条直线的倾斜角α的正切值叫做这条直线的斜率(slope)。通常用小写字母k表示,即 如果使用“倾斜角”这个概念,那么这里的“坡度(比)”实际就是“倾斜角α的正切”.直线的斜率一条直线的倾斜角α的正切值叫做这条直线的斜率.斜率常用小写字母k表示,即直线的斜率如:倾斜角α=45°时,直线的斜率k=tan45° =1;倾斜角α=135°时,直线的斜率k=tan135° =-1.倾斜角为锐角时,k>0;
倾斜角为钝角时,k<0;
倾斜角为0°时,k=0.倾斜角为直角时,k=?当倾斜角α=1200,1350,1500时,这条直线的斜率分别等于多少? 思考:当倾斜角α=00,300,450,600时,这条直线的斜率分别等于多少? 当α∈[0°,90°)时,斜率越大,倾斜角越大;当α∈(90°,180°)时,斜率越大,倾斜角越大.下列哪些说法是正确的( )A 、任一条直线都有倾斜角,也都有斜率
B、直线的倾斜角越大,斜率也越大
C 、平行于x轴的直线的倾斜角是0或π
D 、两直线的倾斜角相等,它们的斜率也相等
E 、两直线的斜率相等,它们的倾斜角也相等
F 、直线斜率的范围是R
G、过原点的直线,斜率越大,越靠近y轴。E、F创新47页想一想我们知道,两点也可以唯一确定一条直线。问题:
如果知道直线上的两点,怎么样来求直线的斜率(倾斜角)呢?如图,当α为锐角时, 锐角 探究新知:由两点确定的直线的斜率
能不能构造一个直角三角形去求?如图,当α为钝角时, 钝角 当 的位置对调时, 值又如何呢? 想一想?同样,当 的方向向上时,也有 当直线 与 x轴平行或重合时,上述式子还成立吗?为什么? 成立,因为分子为0,分母不为0,K=0。 当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?答:斜率不存在, 因为分母为0。对公式的
深入理解经过两点 的直线的斜率公式为:直线的斜率公式(1)已知直线上两点 A(a1, a2),B(b1, b2) ,运用上述公式计算直线AB斜率时,与A,B两点坐标的顺序有关吗?无关(2)当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?不适用经过两点P1(x1, y1),P2(x2, y2) (x1 ≠x2)的直线的斜率公式思考(3)当直线平行于x轴,或与x轴重合时,上述式子还适用吗?为什么?适用0°< < 90°= 90°90°< <180°= 0°k=0k >0k不存在k<0例1 如图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.解:直线AB的斜率直线BC的斜率直线CA的斜率由 及 知,直线AB 与CA的倾斜角均为锐角;由 知,直线BC的倾斜角为钝角.练习:课本86页 2练习:课本86页 3练习:课本89页 A3练习:课本89页 A5例2、在平面直角坐标系中,画出经过原点且斜率分别为1,-1,2和-3的直线 解:(待定系数法)设直线上另一点A1(1,y)则:所以过原点和A1 (1,1)
画直线即可说明:也可设其它特殊点创新47页
创新48页活页规范训练2.在下列四个命题中,正确的命题共有( ).
①坐标平面内的任何一条直线均有倾斜角与斜率;
②直线的倾斜角的取值范围为[0°,180°];
③若一直线的斜率为tan α,则此直线的倾斜角为α;
④若一直线的倾斜角为α,则此直线的斜率为tan α.
A.0个 B.1个 C.2个 D.3个
解析 由于当倾斜角为90°时,其斜率不存在,故命题①、④不正确;由直线倾斜角的定义知;倾斜角的取值范围为[0°,180°),而不是[0°,180°],故命题②不正确;直线的斜率可以是tan 210°,但其倾斜角是30°,而不是210°,所以命题③也不正确.
根据以上判断,四个命题均不正确,故应选择A.
答案 A4.若直线AB与y轴的夹角为60°,则直线AB的倾斜角为________,斜率为________.
解析 如右图,直线AB的倾斜角为30°或150°.
答案 30°或150° 或-6.已知点A(1,2),在坐标轴上求一点P,使直线PA的倾斜角为60°.
解 ①当点P在x轴上时,设点P(a,0),∵A(1,2),
∴k= = .
又∵直线PA的倾斜角为60°,
∴tan 60°= .解得a=1- .
∴点P的坐标为(1- ,0).
②当点P在y轴上时,设点P(0,b),
同理可得b=2- ,
∴点P的坐标为(0,2- ).7.(2012·温州高一检测)设直线l过原点,其倾斜角为α,将直线l绕坐标原点沿逆时针方向旋转45°,得到直线l1,则直线l1的倾斜角为( ).
A.α+45°B.α-135°C.135°-α
D.当0°≤α<135°时,为α+45°;当135°≤α<180°时,为α-135°答案 D11.a为何值时,过点A( 2a,3)、B(2,-1)的直线的倾斜角是锐角?是钝角?是直角?
解 因为过A、B的直线的倾斜角为锐角,所以kAB>0,根据斜率公式得kAB= = >0,∴a>1,同理,当倾斜角为钝角时,kAB<0,
即 <0,∴a<1,当倾斜角为直角时,A、B两点的横坐标相等,即2a=2,∴a=1.
故:当a>1时,直线的倾斜角是锐角;
当a<1时,直线的倾斜角是钝角;
当a=1时,直线的倾斜角是直角.9.直线l过点A(1,2),且不过第四象限,那么直线l的斜率的取值范围是________.
答案 [0,2]12.(创新拓展)点M(x,y)在函数y=-2x+8图象上,当x∈[2,5]时,求 的取值范围.
解 = 的几何意义是过M(x,y),N(-1,-1)两点的直线的斜率.点M在2≤x≤5上的直线y=-2x+8的线段AB上运动,其中A(2,4),B(5,-2).由于kNA= ,kNB=- ,
∴- ≤ ≤ .∴的取值范围为 .
一点能确定一条直线的位置吗?已知直线l 经过点P,直线l 的位置能够确定吗?过一点有无数条直线,故一点不能确定直线。P 与x轴正方向形成45度角的直线有几条? P.
在平面直角坐标系中,确定一条直线位置的条件是:已知直线上的一个点和这条直线的方向。而直线的方向我们就是用倾斜角来刻画的。 当直线 l 与x轴相交时,我们取x轴作为基准,x轴正向与直线 l 向上方向之间所成的角α 叫做直线 l 的倾斜角(angle of inclination) .xyOl 当直线l与x轴平行或重合时,规定它的倾斜角为 .直线的倾斜角 的取值范围为:直线的倾斜角P.我们把 和 角就叫做直线 与 的倾斜角。下列各图中标出的角α是直线的倾斜角吗? oα注意: (1)直线向上方向;
(2)轴的正方向。(1)看看这三条直线,它们倾斜角
的大小关系是什么?l1l2l3(2)你认为下列说法对吗?
①所有的直线都有唯一确定的倾斜角与它对应;
②每一个倾斜角都对应于唯一的一条直线.直线的倾斜程度与倾斜角有什么关系? 平面直角坐标系中每一条直线都有确定的倾斜角,倾斜程度不同的直线有不同的倾斜角,倾斜程度相同的直线其倾斜角相同。 思考 只知道直线的倾斜角α,不能确定一条直线的位置。 已知直线上的一个点不能确定一条直线的位置,那已知直线的倾斜角α,能不能确定一条直线的位置? 确定平面直角坐标系中一条直线位置的几何要素是:
直线上的一个定点以及它的倾斜角, 二者缺一不可.确定直线的要素 日常生活中,还有没有表示
倾斜程度的量?(即倾斜角a的正切值) 一条直线的倾斜角α的正切值叫做这条直线的斜率(slope)。通常用小写字母k表示,即 如果使用“倾斜角”这个概念,那么这里的“坡度(比)”实际就是“倾斜角α的正切”.直线的斜率一条直线的倾斜角α的正切值叫做这条直线的斜率.斜率常用小写字母k表示,即直线的斜率如:倾斜角α=45°时,直线的斜率k=tan45° =1;倾斜角α=135°时,直线的斜率k=tan135° =-1.倾斜角为锐角时,k>0;
倾斜角为钝角时,k<0;
倾斜角为0°时,k=0.倾斜角为直角时,k=?当倾斜角α=1200,1350,1500时,这条直线的斜率分别等于多少? 思考:当倾斜角α=00,300,450,600时,这条直线的斜率分别等于多少? 当α∈[0°,90°)时,斜率越大,倾斜角越大;当α∈(90°,180°)时,斜率越大,倾斜角越大.下列哪些说法是正确的( )A 、任一条直线都有倾斜角,也都有斜率
B、直线的倾斜角越大,斜率也越大
C 、平行于x轴的直线的倾斜角是0或π
D 、两直线的倾斜角相等,它们的斜率也相等
E 、两直线的斜率相等,它们的倾斜角也相等
F 、直线斜率的范围是R
G、过原点的直线,斜率越大,越靠近y轴。E、F创新47页想一想我们知道,两点也可以唯一确定一条直线。问题:
如果知道直线上的两点,怎么样来求直线的斜率(倾斜角)呢?如图,当α为锐角时, 锐角 探究新知:由两点确定的直线的斜率
能不能构造一个直角三角形去求?如图,当α为钝角时, 钝角 当 的位置对调时, 值又如何呢? 想一想?同样,当 的方向向上时,也有 当直线 与 x轴平行或重合时,上述式子还成立吗?为什么? 成立,因为分子为0,分母不为0,K=0。 当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?答:斜率不存在, 因为分母为0。对公式的
深入理解经过两点 的直线的斜率公式为:直线的斜率公式(1)已知直线上两点 A(a1, a2),B(b1, b2) ,运用上述公式计算直线AB斜率时,与A,B两点坐标的顺序有关吗?无关(2)当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?不适用经过两点P1(x1, y1),P2(x2, y2) (x1 ≠x2)的直线的斜率公式思考(3)当直线平行于x轴,或与x轴重合时,上述式子还适用吗?为什么?适用0°< < 90°= 90°90°< <180°= 0°k=0k >0k不存在k<0例1 如图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.解:直线AB的斜率直线BC的斜率直线CA的斜率由 及 知,直线AB 与CA的倾斜角均为锐角;由 知,直线BC的倾斜角为钝角.练习:课本86页 2练习:课本86页 3练习:课本89页 A3练习:课本89页 A5例2、在平面直角坐标系中,画出经过原点且斜率分别为1,-1,2和-3的直线 解:(待定系数法)设直线上另一点A1(1,y)则:所以过原点和A1 (1,1)
画直线即可说明:也可设其它特殊点创新47页
创新48页活页规范训练2.在下列四个命题中,正确的命题共有( ).
①坐标平面内的任何一条直线均有倾斜角与斜率;
②直线的倾斜角的取值范围为[0°,180°];
③若一直线的斜率为tan α,则此直线的倾斜角为α;
④若一直线的倾斜角为α,则此直线的斜率为tan α.
A.0个 B.1个 C.2个 D.3个
解析 由于当倾斜角为90°时,其斜率不存在,故命题①、④不正确;由直线倾斜角的定义知;倾斜角的取值范围为[0°,180°),而不是[0°,180°],故命题②不正确;直线的斜率可以是tan 210°,但其倾斜角是30°,而不是210°,所以命题③也不正确.
根据以上判断,四个命题均不正确,故应选择A.
答案 A4.若直线AB与y轴的夹角为60°,则直线AB的倾斜角为________,斜率为________.
解析 如右图,直线AB的倾斜角为30°或150°.
答案 30°或150° 或-6.已知点A(1,2),在坐标轴上求一点P,使直线PA的倾斜角为60°.
解 ①当点P在x轴上时,设点P(a,0),∵A(1,2),
∴k= = .
又∵直线PA的倾斜角为60°,
∴tan 60°= .解得a=1- .
∴点P的坐标为(1- ,0).
②当点P在y轴上时,设点P(0,b),
同理可得b=2- ,
∴点P的坐标为(0,2- ).7.(2012·温州高一检测)设直线l过原点,其倾斜角为α,将直线l绕坐标原点沿逆时针方向旋转45°,得到直线l1,则直线l1的倾斜角为( ).
A.α+45°B.α-135°C.135°-α
D.当0°≤α<135°时,为α+45°;当135°≤α<180°时,为α-135°答案 D11.a为何值时,过点A( 2a,3)、B(2,-1)的直线的倾斜角是锐角?是钝角?是直角?
解 因为过A、B的直线的倾斜角为锐角,所以kAB>0,根据斜率公式得kAB= = >0,∴a>1,同理,当倾斜角为钝角时,kAB<0,
即 <0,∴a<1,当倾斜角为直角时,A、B两点的横坐标相等,即2a=2,∴a=1.
故:当a>1时,直线的倾斜角是锐角;
当a<1时,直线的倾斜角是钝角;
当a=1时,直线的倾斜角是直角.9.直线l过点A(1,2),且不过第四象限,那么直线l的斜率的取值范围是________.
答案 [0,2]12.(创新拓展)点M(x,y)在函数y=-2x+8图象上,当x∈[2,5]时,求 的取值范围.
解 = 的几何意义是过M(x,y),N(-1,-1)两点的直线的斜率.点M在2≤x≤5上的直线y=-2x+8的线段AB上运动,其中A(2,4),B(5,-2).由于kNA= ,kNB=- ,
∴- ≤ ≤ .∴的取值范围为 .
