2022年人教版小学数学四年级下册第7单元图形的 单元练习(word版 含解析)
文档属性
| 名称 | 2022年人教版小学数学四年级下册第7单元图形的 单元练习(word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 901.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-23 11:06:04 | ||
图片预览


文档简介
2022年人教版小学数学四年级下册
第7单元 图形的运动(二) 单元练习
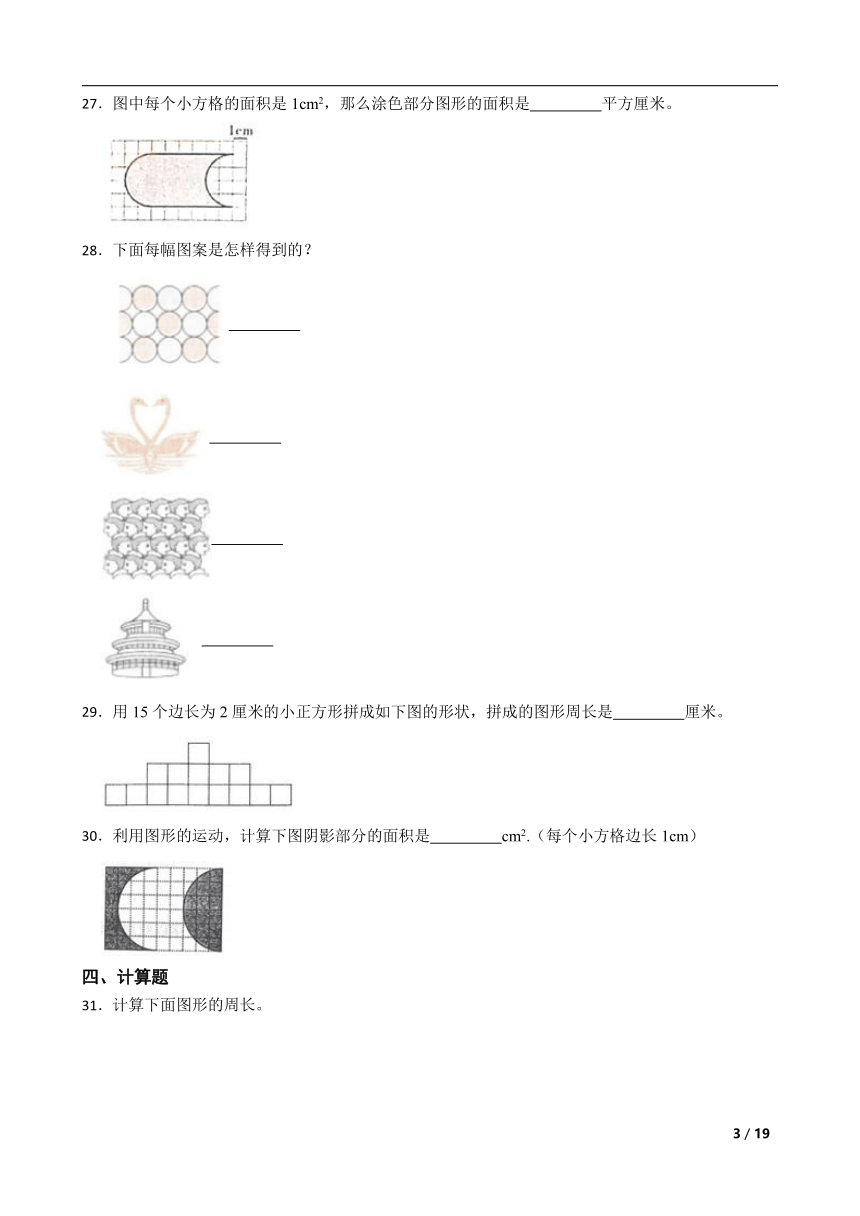
一、单选题
1.( )不一定是轴对称图形。
A.长方形 B.正方形 C.三角形
2.下面图( )不是轴对称图形。
A. B. C.
3.一只蚂蚁从A点开始慢慢爬回家里,它有两条路线可以选择,蚂蚁回家所花的时间( )。
A.①号路线时间长 B.②号路线时间长 C.一样长
4. 是从下图( )张纸上剪出来的。
A. B. C.
5.以下图形中,不是轴对称图形的是( )。
A. B. C. D.
6.下面图形中,( )不是轴对称图形。
A. B. C.
7.下面图形中,( )能找到的对称轴最多。
A. B. C.
8.下列说法中正确的是( )
A.直角三角形一定是轴对称图形。
B.等边三角形有3条对称轴。
C.两个完全一样的三角形组成的图形一定是轴对称图形
D.平行四边形是轴对称图形,它有1条对称轴。
9.下面的图形中,对称轴条数最少的是( )。
A.长方形 B.等边三角形 C.正方形 D.圆
10.下列关于圆的说法正确的是( )。
A.半径确定圆的位置 B.圆是轴对称图形
C.圆周率是周长与半径的比值 D.圆的对称轴是直径
二、判断题
11.人体内部器官图象是轴对称图形。( )
12. 是从 对折后的纸上剪下来的图形。( )
13.五角星是轴对称图形,它只有1条对称轴。( )
14. 这个长方形有4条对称轴。( )
15.轴对称图形中,对应点到对称轴的距离相等。( )
16.圆是轴对称图形,有无数条对称轴,每条对称轴都过圆心.( )
17.圆、长方形、正方形、三角形都是轴对称图形。( )
18.梯形不可能是轴对称图形。( )
19.字母A不是轴对称图形。( )
20.圆形有无数条对称轴。( )
三、填空题
21.长方形、正方形,平行四边形中不是轴对称图形的是 。
22.正方形有 条对称轴,长方形有 条对称轴,圆形有 条对称轴。
23. 左图中有 条对称轴;如果圆的半径是3cm,那么每个圆的周长是 cm,长方形的周长是 cm。
24.长方形有 条对称轴,平行四边形有 条对称轴,等边三角形有 条对称轴。
25.正方形是轴对称图形,它有 条对称轴。
26.长方形有 条对称轴,正方形有 条对称轴,圆形有 条对称轴。
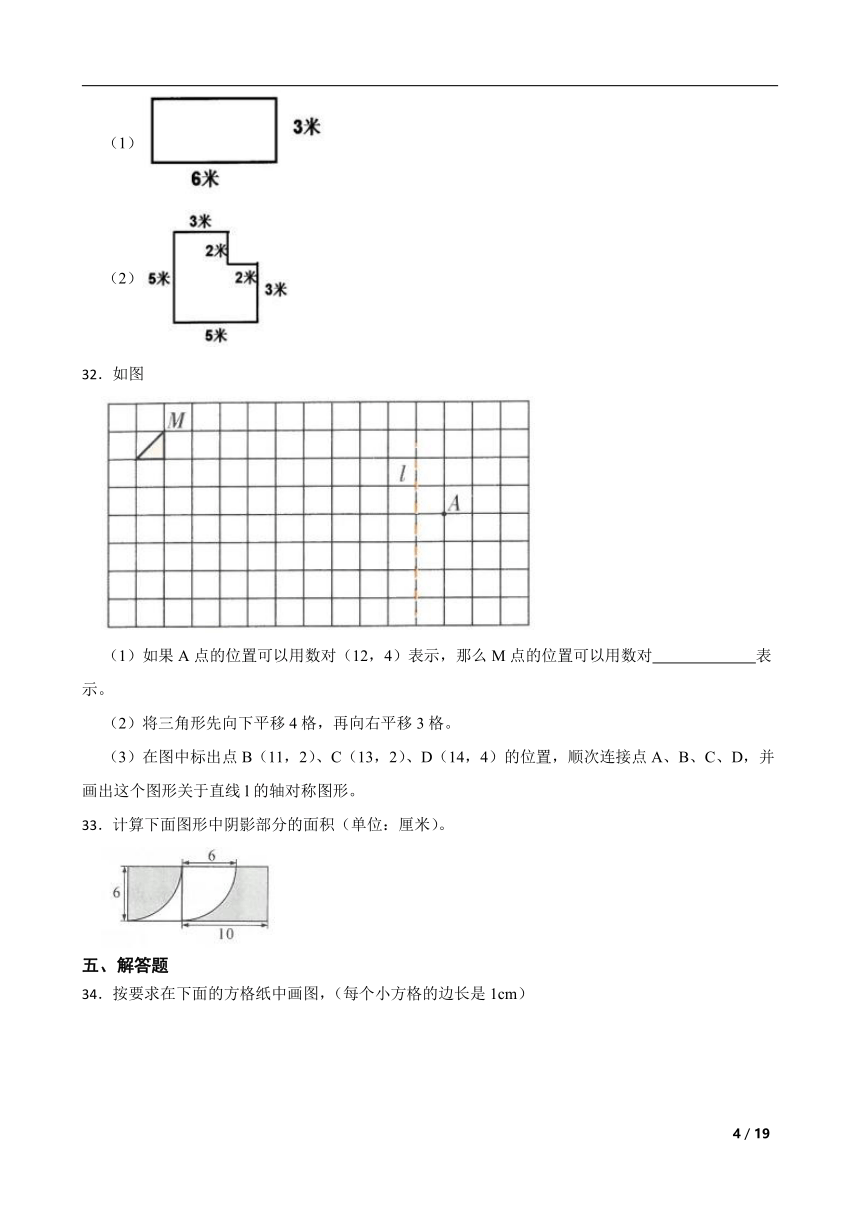
27.图中每个小方格的面积是1cm2,那么涂色部分图形的面积是 平方厘米。
28.下面每幅图案是怎样得到的?
29.用15个边长为2厘米的小正方形拼成如下图的形状,拼成的图形周长是 厘米。
30.利用图形的运动,计算下图阴影部分的面积是 cm2.(每个小方格边长1cm)
四、计算题
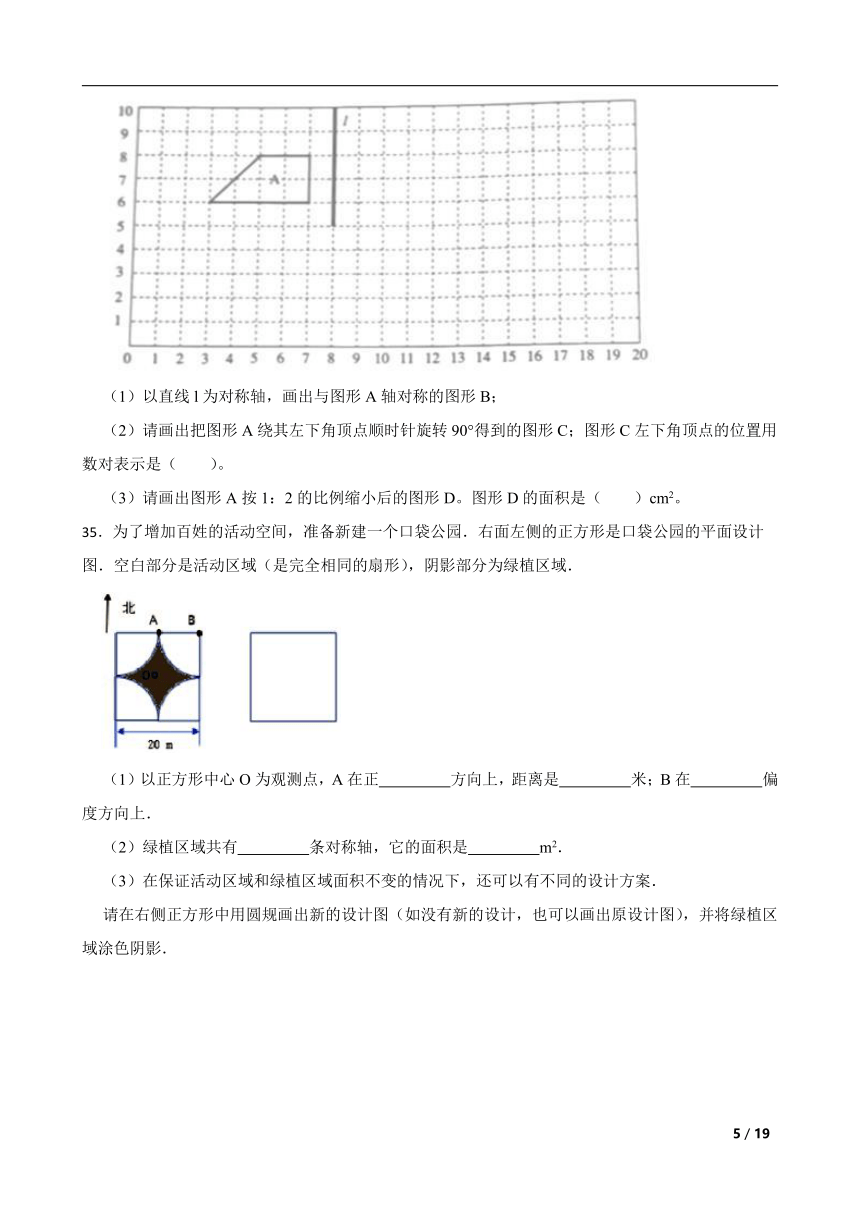
31.计算下面图形的周长。
(1)
(2)
32.如图
(1)如果A点的位置可以用数对(12,4)表示,那么M点的位置可以用数对 表示。
(2)将三角形先向下平移4格,再向右平移3格。
(3)在图中标出点B(11,2)、C(13,2)、D(14,4)的位置,顺次连接点A、B、C、D,并画出这个图形关于直线l的轴对称图形。
33.计算下面图形中阴影部分的面积(单位:厘米)。
五、解答题
34.按要求在下面的方格纸中画图,(每个小方格的边长是1cm)
(1)以直线l为对称轴,画出与图形A轴对称的图形B;
(2)请画出把图形A绕其左下角顶点顺时针旋转90°得到的图形C;图形C左下角顶点的位置用数对表示是( )。
(3)请画出图形A按1:2的比例缩小后的图形D。图形D的面积是( )cm2。
35.为了增加百姓的活动空间,准备新建一个口袋公园.右面左侧的正方形是口袋公园的平面设计图.空白部分是活动区域(是完全相同的扇形),阴影部分为绿植区域.
(1)以正方形中心O为观测点,A在正 方向上,距离是 米;B在 偏 度方向上.
(2)绿植区域共有 条对称轴,它的面积是 m2.
(3)在保证活动区域和绿植区域面积不变的情况下,还可以有不同的设计方案.
请在右侧正方形中用圆规画出新的设计图(如没有新的设计,也可以画出原设计图),并将绿植区域涂色阴影.
答案解析部分
1.【答案】C
【考点】轴对称
【解析】【解答】解:三角形不一共是轴对称图形。
故答案为:C。
【分析】轴对称图形是指平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形。
2.【答案】C
【考点】轴对称
【解析】【解答】解:图三不是轴对称图形。
故答案为:C。
【分析】依据轴对称图形的定义判断:平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这个图形就是轴对称图形。
3.【答案】C
【考点】利用平移巧算图形周长与面积
【解析】【解答】解:蚂蚁回家所花的时间一样长。
故答案为:C。
【分析】将②号路线的短边平移到最外面,就形成了一个长方形,所以①号路线和②号路线一样长,那么用的时间也一样长。
4.【答案】C
【考点】轴对称
【解析】【解答】解:是从下图C张纸上剪出来的。
故答案为:C。
【分析】叶子的一半就是纸上剪掉的图形,据此解答。
5.【答案】B
【考点】轴对称
【解析】【解答】选项A,是轴对称图形;
选项B,不是轴对称图形;
选项C,是轴对称图形;
选项D,是轴对称图形。
故答案为:B。
【分析】如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫对称轴;判断一个图形是否是轴对称图形,关键是找它的对称轴,要想象沿着这条线翻折能不能重叠,据此解答。
6.【答案】B
【考点】轴对称
【解析】【解答】A选项:正方形,是轴对称图形;
B选项:平行四边形,不是轴对称图形;
C选项:圆,是轴对称图形;
故答案为:B。
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,据此判断选项图形即可。
7.【答案】C
【考点】轴对称图形的对称轴数量及位置
【解析】【解答】解:长方形有2条对称轴;
等边三角形有3条对称轴;
圆环有无数条对称轴。
故答案为:C。
【分析】如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形,折痕所在的这条直线叫做对称轴。
8.【答案】B
【考点】轴对称;轴对称图形的对称轴数量及位置
【解析】【解答】解:选项A,直角三角形不一定是轴对称图形;
选项B,等边三角形有3条对称轴;
选项C,两个完全一样的三角形组成的图形不一定是轴对称图形;
选项D,平行四边形不是轴对称图形,没有对称轴。
故答案为:B。
【分析】轴对称图形,是指在平面内沿一条直线折叠,直线两旁的部分能够完全重合的图形,这条直线就叫做对称轴。
选项A,等腰直角三角形是轴对称图形;选项B,等边三角形是轴对称图形;选项C和选项D,两个完全一样的三角形能组成一个平行四边形,平行四边形不是轴对称图形,没有对称轴。
9.【答案】A
【考点】轴对称图形的对称轴数量及位置
【解析】【解答】选项A,长方形有2条对称轴;
选项B,等边三角形有3条对称轴;
选项C,正方形有4条对称轴;
选项D,圆有无数条对称轴。
故答案为:A。
【分析】如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫对称轴;判断一个图形是否是轴对称图形,关键是找它的对称轴,要想象沿着这条线翻折能不能重叠,据此分别数一数各选项的图形对称轴条数,然后对比即可。
10.【答案】B
【考点】轴对称;圆、圆心、半径与直径的认识;圆的周长
【解析】【解答】解:选项A,圆心确定圆的位置,即说法错误;
选项B,圆是轴对称图形,说法正确;
选项C,圆周率=圆的周长÷圆的直径,所以圆周率是周长与直径的比值,即说法错误;
选项D,圆的对称轴是圆的直径所在的直线,即说法错误。
故答案为:B。
【分析】圆心确定圆的位置,半径确定圆的大小,据此即可判断选项A;
轴对称图形,是指在平面内沿一条直线折叠,直线两旁的部分能够完全重合的图形,这条直线就叫做对称轴,即可判断选项B;
圆的周长=圆周率×圆的直径(2×圆的半径),即可得出圆周率、圆的周长以及圆的直径之间的关系,即可判断选项C;
圆的直径是线段,圆的对称轴是直线,即可判断出选项D。
11.【答案】(1)错误
【考点】轴对称
【解析】【解答】解:人体内部器官图像不是轴对称图形。原题说法错误。
故答案为:错误。
【分析】人体内部左右里面是不相同的,所以人体内部器官图像不是轴对称图形。
12.【答案】(1)正
【考点】轴对称
【解析】【解答】解: 是从 对折后的纸上剪下来的图形。
故答案为:正确。
【分析】把左边的图形沿着对称轴折叠,其中,左半部分就是与之对应的右面纸上剪下来的。
13.【答案】(1)错误
【考点】轴对称图形的对称轴数量及位置
【解析】【解答】解:五角星是轴对称图形,它有5条对称轴。原题说法错误。
故答案为:错误。
【分析】五角星的对称轴如图:
14.【答案】(1)错误
【考点】轴对称图形的对称轴数量及位置
【解析】【解答】解:长方形有2条对称轴,所以说法错误。
故答案为:错误。
【分析】轴对称图形,是指在平面内沿一条直线折叠,直线两旁的部分能够完全重合的图形,这条直线就叫做对称轴。长方形只有对应两边中点的连线是对称轴。
15.【答案】(1)正
【考点】轴对称
【解析】【解答】 轴对称图形中,对应点到对称轴的距离相等,此题说法正确。
故答案为:正确。
【分析】在轴对称图形中,对称轴两侧相对应的点到对称轴的距离相等,据此判断。
16.【答案】(1)正
【考点】轴对称图形的对称轴数量及位置
【解析】【解答】解:圆是轴对称图形,有无数条对称轴,直径所在的直线就是对称轴,所以每条对称轴都过圆心。
故答案为:正确。
【分析】圆是轴对称图形,有无数条对称轴,直径所在的直线就是对称轴,圆的直径有无数条,所以每条对称轴都过圆心。
17.【答案】(1)错误
【考点】轴对称
【解析】【解答】解:圆、长方形、正方形都是轴对称图形,三角形不一定是轴对称图形。
故答案为:错误。
【分析】不规则三角形不是轴对称图形。
18.【答案】(1)错误
【考点】轴对称;梯形的特征及分类
【解析】【解答】梯形可能是轴对称图形,等腰梯形是轴对称图形。
故答案为:错误。
【分析】如果一个图形沿着一条直线对折后两部分完全重合,那这样的图形就叫做轴对称图形,据此解答。
19.【答案】(1)错误
【考点】轴对称
【解析】【解答】字母A是轴对称图形。原题说法错误。
故答案为:错误。
【分析】一个图形沿着一条直线对折后两边能够完全重合,这个图形就是轴对称图形。
20.【答案】(1)正
【考点】轴对称图形的对称轴数量及位置
【解析】【解答】圆形有无数条对称轴。原题说法正确。
故答案为:正确。
【分析】一个圆形沿着过圆心的任意一条直线对折后两边都能完全重合,所以圆有无数条对称轴。
21.【答案】平行四边形
【考点】轴对称
【解析】【解答】长方形、正方形,平行四边形中不是轴对称图形的是平行四边形。
故答案为:平行四边形。
【分析】如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形。
22.【答案】4;2;无数
【考点】轴对称图形的对称轴数量及位置
【解析】【解答】解:正方形有4条对称轴,长方形有2条对称轴,圆形有无数条对称轴。
故答案为:4;2;无数。
【分析】轴对称图形是指平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形,其中这条直线叫做对称轴。
23.【答案】两;18.84;36
【考点】长方形的周长;轴对称图形的对称轴数量及位置;圆的周长
【解析】【解答】 左图中有两条对称轴;
如果圆的半径是3cm,那么每个圆的周长是3.14×3×2=18.84(cm),长方形的周长是(3×4+3×2)×2=36(cm)。
故答案为:两;18.84;36。
【分析】观察图可知,这个图形是由长方形与两个圆组合成的,有两条对称轴,分别是两条长和两条宽的中点所在的直线;
已知圆的半径,要求圆的周长,用公式:C=2πr,据此列式解答;
观察图可知,长方形的长是圆的半径的4倍,宽是圆的半径的2倍,先求出长方形的长与宽,然后用公式:长方形的周长=(长+宽)×2,据此列式解答。
24.【答案】2;0;3
【考点】轴对称图形的对称轴数量及位置
【解析】【解答】解:长方形有2条对称轴,平行四边形有0条对称轴,等边三角形有3条对称轴。
故答案为:2;0;3。
【分析】 轴对称图形,是指在平面内沿一条直线折叠,直线两旁的部分能够完全重合的图形,这条直线就叫做对称轴。本题中长方形的对称轴为两组对边中点的连线;平行四边形没有对称轴;等边三角形的三条中线是对称轴,本题据此解答。
25.【答案】4
【考点】轴对称图形的对称轴数量及位置
【解析】【解答】因为正方形沿两组对边的中线及其对角线所在的直线对折,对折后的两部分都能完全重合,
则正方形是轴对称图形,两组对边的中线及其对角线所在的直线就是其对称轴,
所以说正方形有4条对称轴.
故答案为:4.
【分析】轴对称图形,是指在平面内沿一条直线折叠,直线两旁的部分能够完全重合的图形,这条直线就叫做对称轴。本题中将正方形折叠使其两部分完全重合,找出这样的所有直线,即可得出答案。
26.【答案】2;4;无数
【考点】轴对称图形的对称轴数量及位置
【解析】【解答】 长方形有2条对称轴,正方形有4条对称轴,圆形有无数条对称轴。
故答案为:2;4;无数。
【分析】如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫对称轴;判断一个图形是否是轴对称图形,关键是找它的对称轴,要想象沿着这条线翻折能不能重叠,据此找出题中各图形的对称轴。
27.【答案】24
【考点】利用平移巧算图形周长与面积
【解析】【解答】解:6×4=24(平方厘米)
故答案为:24。
【分析】用平移的方法,把左边的半圆向右平移6格,就变成了一个长6厘米,宽4厘米的长方形,用长×宽就得出了涂色部分的面积。
28.【答案】轴对称;轴对称;平移;轴对称
【考点】轴对称;平移与平移现象
【解析】【解答】解:
故答案为:轴对称;轴对称;平移;轴对称。
【分析】如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形,折痕所在的这条直线叫做对称轴;
物体或图形沿着某个方向移动了一定距离叫做平移。特点:大小、形状、方向不变,位置变化。
29.【答案】48
【考点】利用平移巧算图形周长与面积
【解析】【解答】解:9×2=18(厘米)
3×2=6(厘米)
(18+6)×2
=24×2
=48(厘米)
故答案为:48。
【分析】通过平移把这个图形的周长变成长18厘米,宽6厘米的长方形,长方形的周长=(长+宽)×2。
30.【答案】24
【考点】利用平移巧算图形周长与面积
【解析】【解答】解:6×4=24(cm2)
故答案为:24。
【分析】利用平移的方法, 阴影部分变成一个长方形,长方形的面积=长×宽。
31.【答案】(1)(6+3)×2=18(米)
(2)5×4=20(米)
【考点】长方形的周长;利用平移巧算图形周长与面积
【解析】【分析】(1)长方形周长=(长+宽)×2,据此解答;
(2)把右上角的两条短边向右向上平移,刚好是一个正方形,正方形周长=边长×4。
32.【答案】(1)(2,7)
(2)解:如图所示:
(3)解:如图所示:
【考点】作平移后的图形
【解析】【分析】(1)用数对表示位置时,前面一个数表示第几列,后面一个数表示第几行;
(2)作平移图形的方法:先确定要平移图形的关键点,确定平移的方向是朝哪移的,然后确定移动的长度(格子数),最后把各点连接成图;
(3)画轴对称图形的方法是:数出或量出图形的关键点到对称轴的距离,在对称轴的另一侧找出关键点的对应点,按照所给图形的顺序连接各点。
33.【答案】解:10×6=60(平方厘米)
答:阴影部分面积是60平方厘米。
【考点】长方形的面积;利用平移巧算图形周长与面积
【解析】【分析】把左边阴影部分向右平移与右边的阴影部分组合成一个长方形,长是10厘米、宽是6厘米,根据长方形面积公式计算阴影部分的总面积即可。
34.【答案】(1)
(2)
图形C左下角顶点的位置用数对表示是(3, 2)。
(3)
图形D的面积是(1.5)cm2。
【考点】图形的缩放;补全轴对称图形;作旋转后的图形
【解析】【解答】(1)如图所示:
(2)如图所示:
图形C左下角顶点的位置用数对表示是(3,2)。
(3)如图所示:
(1+2)×1÷2=1.5(cm2)。
故答案为:(1)
(2)
图形C左下角顶点的位置用数对表示是(3,2);
(3)
图形D的面积是(1.5)cm2。
【分析】 (1)已知图形A,在对称轴另一侧找到图形A对应个点,依次连接各点,由此画出轴对称图形B;
(2)以图形A左下角顶点为旋转中心,找出各点顺时针旋转90°后的对应点,再将这几个点依次连接,由此可以画出旋转后的图形C ;
(3)缩小后的图形D与原图形A对应线段长的比为1:2,原图各边长除以2,得到缩小后各边长度,梯形面积=(上底+下底)×高÷2,据此解答。
35.【答案】(1)北;10;东;北45
(2)4;86
(3)解:
【考点】轴对称图形的对称轴数量及位置;根据方向和距离确定物体的位置;圆的面积
【解析】【分析】(1)根据方向标,平面图上上北下南、左西右东,正方形边长是20,所以A距中心O的距离是10m,因为扇形的面积完全一样,所以A是边长的中点,所以B在东偏北45度方向上;
(2)四个扇形的圆心角都是90度,且半径都相等,所以4个扇形正好构成一个半径是10m的圆,阴影的面积=正方形的面积-圆的面积=20×20-π×102=400-314=86m2;
(3)把外围的扇形移动到中间拼成一个半径是10m的圆,也就是以中心点O为圆心,10m为半径画一个圆,剩余是绿植的部分。
试题分析部分
1、试卷总体分布分析
总分:113分
分值分布 客观题(占比) 58.0(51.3%)
主观题(占比) 55.0(48.7%)
题量分布 客观题(占比) 29(82.9%)
主观题(占比) 6(17.1%)
2、试卷题量分布分析
大题题型 题目量(占比) 分值(占比)
填空题 10(28.6%) 21.0(18.6%)
解答题 2(5.7%) 26.0(23.0%)
计算题 3(8.6%) 26.0(23.0%)
单选题 10(28.6%) 20.0(17.7%)
判断题 10(28.6%) 20.0(17.7%)
3、试卷难度结构分析
序号 难易度 占比
1 普通 (91.4%)
2 困难 (8.6%)
4、试卷知识点分析
序号 知识点(认知水平) 分值(占比) 对应题号
1 作旋转后的图形 15.0(13.3%) 34
2 圆的周长 5.0(4.4%) 10,23
3 长方形的面积 5.0(4.4%) 33
4 作平移后的图形 11.0(9.7%) 32
5 平移与平移现象 4.0(3.5%) 28
6 根据方向和距离确定物体的位置 11.0(9.7%) 35
7 利用平移巧算图形周长与面积 20.0(17.7%) 3,27,29,30,31,33
8 轴对称 31.0(27.4%) 1,2,4,5,6,8,10,11,12,15,17,18,19,21,28
9 轴对称图形的对称轴数量及位置 38.0(33.6%) 7,8,9,13,14,16,20,22,23,24,25,26,35
10 补全轴对称图形 15.0(13.3%) 34
11 圆的面积 11.0(9.7%) 35
12 梯形的特征及分类 2.0(1.8%) 18
13 长方形的周长 13.0(11.5%) 23,31
14 圆、圆心、半径与直径的认识 2.0(1.8%) 10
15 图形的缩放 15.0(13.3%) 34
1 / 19
第7单元 图形的运动(二) 单元练习
一、单选题
1.( )不一定是轴对称图形。
A.长方形 B.正方形 C.三角形
2.下面图( )不是轴对称图形。
A. B. C.
3.一只蚂蚁从A点开始慢慢爬回家里,它有两条路线可以选择,蚂蚁回家所花的时间( )。
A.①号路线时间长 B.②号路线时间长 C.一样长
4. 是从下图( )张纸上剪出来的。
A. B. C.
5.以下图形中,不是轴对称图形的是( )。
A. B. C. D.
6.下面图形中,( )不是轴对称图形。
A. B. C.
7.下面图形中,( )能找到的对称轴最多。
A. B. C.
8.下列说法中正确的是( )
A.直角三角形一定是轴对称图形。
B.等边三角形有3条对称轴。
C.两个完全一样的三角形组成的图形一定是轴对称图形
D.平行四边形是轴对称图形,它有1条对称轴。
9.下面的图形中,对称轴条数最少的是( )。
A.长方形 B.等边三角形 C.正方形 D.圆
10.下列关于圆的说法正确的是( )。
A.半径确定圆的位置 B.圆是轴对称图形
C.圆周率是周长与半径的比值 D.圆的对称轴是直径
二、判断题
11.人体内部器官图象是轴对称图形。( )
12. 是从 对折后的纸上剪下来的图形。( )
13.五角星是轴对称图形,它只有1条对称轴。( )
14. 这个长方形有4条对称轴。( )
15.轴对称图形中,对应点到对称轴的距离相等。( )
16.圆是轴对称图形,有无数条对称轴,每条对称轴都过圆心.( )
17.圆、长方形、正方形、三角形都是轴对称图形。( )
18.梯形不可能是轴对称图形。( )
19.字母A不是轴对称图形。( )
20.圆形有无数条对称轴。( )
三、填空题
21.长方形、正方形,平行四边形中不是轴对称图形的是 。
22.正方形有 条对称轴,长方形有 条对称轴,圆形有 条对称轴。
23. 左图中有 条对称轴;如果圆的半径是3cm,那么每个圆的周长是 cm,长方形的周长是 cm。
24.长方形有 条对称轴,平行四边形有 条对称轴,等边三角形有 条对称轴。
25.正方形是轴对称图形,它有 条对称轴。
26.长方形有 条对称轴,正方形有 条对称轴,圆形有 条对称轴。
27.图中每个小方格的面积是1cm2,那么涂色部分图形的面积是 平方厘米。
28.下面每幅图案是怎样得到的?
29.用15个边长为2厘米的小正方形拼成如下图的形状,拼成的图形周长是 厘米。
30.利用图形的运动,计算下图阴影部分的面积是 cm2.(每个小方格边长1cm)
四、计算题
31.计算下面图形的周长。
(1)
(2)
32.如图
(1)如果A点的位置可以用数对(12,4)表示,那么M点的位置可以用数对 表示。
(2)将三角形先向下平移4格,再向右平移3格。
(3)在图中标出点B(11,2)、C(13,2)、D(14,4)的位置,顺次连接点A、B、C、D,并画出这个图形关于直线l的轴对称图形。
33.计算下面图形中阴影部分的面积(单位:厘米)。
五、解答题
34.按要求在下面的方格纸中画图,(每个小方格的边长是1cm)
(1)以直线l为对称轴,画出与图形A轴对称的图形B;
(2)请画出把图形A绕其左下角顶点顺时针旋转90°得到的图形C;图形C左下角顶点的位置用数对表示是( )。
(3)请画出图形A按1:2的比例缩小后的图形D。图形D的面积是( )cm2。
35.为了增加百姓的活动空间,准备新建一个口袋公园.右面左侧的正方形是口袋公园的平面设计图.空白部分是活动区域(是完全相同的扇形),阴影部分为绿植区域.
(1)以正方形中心O为观测点,A在正 方向上,距离是 米;B在 偏 度方向上.
(2)绿植区域共有 条对称轴,它的面积是 m2.
(3)在保证活动区域和绿植区域面积不变的情况下,还可以有不同的设计方案.
请在右侧正方形中用圆规画出新的设计图(如没有新的设计,也可以画出原设计图),并将绿植区域涂色阴影.
答案解析部分
1.【答案】C
【考点】轴对称
【解析】【解答】解:三角形不一共是轴对称图形。
故答案为:C。
【分析】轴对称图形是指平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形。
2.【答案】C
【考点】轴对称
【解析】【解答】解:图三不是轴对称图形。
故答案为:C。
【分析】依据轴对称图形的定义判断:平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这个图形就是轴对称图形。
3.【答案】C
【考点】利用平移巧算图形周长与面积
【解析】【解答】解:蚂蚁回家所花的时间一样长。
故答案为:C。
【分析】将②号路线的短边平移到最外面,就形成了一个长方形,所以①号路线和②号路线一样长,那么用的时间也一样长。
4.【答案】C
【考点】轴对称
【解析】【解答】解:是从下图C张纸上剪出来的。
故答案为:C。
【分析】叶子的一半就是纸上剪掉的图形,据此解答。
5.【答案】B
【考点】轴对称
【解析】【解答】选项A,是轴对称图形;
选项B,不是轴对称图形;
选项C,是轴对称图形;
选项D,是轴对称图形。
故答案为:B。
【分析】如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫对称轴;判断一个图形是否是轴对称图形,关键是找它的对称轴,要想象沿着这条线翻折能不能重叠,据此解答。
6.【答案】B
【考点】轴对称
【解析】【解答】A选项:正方形,是轴对称图形;
B选项:平行四边形,不是轴对称图形;
C选项:圆,是轴对称图形;
故答案为:B。
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,据此判断选项图形即可。
7.【答案】C
【考点】轴对称图形的对称轴数量及位置
【解析】【解答】解:长方形有2条对称轴;
等边三角形有3条对称轴;
圆环有无数条对称轴。
故答案为:C。
【分析】如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形,折痕所在的这条直线叫做对称轴。
8.【答案】B
【考点】轴对称;轴对称图形的对称轴数量及位置
【解析】【解答】解:选项A,直角三角形不一定是轴对称图形;
选项B,等边三角形有3条对称轴;
选项C,两个完全一样的三角形组成的图形不一定是轴对称图形;
选项D,平行四边形不是轴对称图形,没有对称轴。
故答案为:B。
【分析】轴对称图形,是指在平面内沿一条直线折叠,直线两旁的部分能够完全重合的图形,这条直线就叫做对称轴。
选项A,等腰直角三角形是轴对称图形;选项B,等边三角形是轴对称图形;选项C和选项D,两个完全一样的三角形能组成一个平行四边形,平行四边形不是轴对称图形,没有对称轴。
9.【答案】A
【考点】轴对称图形的对称轴数量及位置
【解析】【解答】选项A,长方形有2条对称轴;
选项B,等边三角形有3条对称轴;
选项C,正方形有4条对称轴;
选项D,圆有无数条对称轴。
故答案为:A。
【分析】如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫对称轴;判断一个图形是否是轴对称图形,关键是找它的对称轴,要想象沿着这条线翻折能不能重叠,据此分别数一数各选项的图形对称轴条数,然后对比即可。
10.【答案】B
【考点】轴对称;圆、圆心、半径与直径的认识;圆的周长
【解析】【解答】解:选项A,圆心确定圆的位置,即说法错误;
选项B,圆是轴对称图形,说法正确;
选项C,圆周率=圆的周长÷圆的直径,所以圆周率是周长与直径的比值,即说法错误;
选项D,圆的对称轴是圆的直径所在的直线,即说法错误。
故答案为:B。
【分析】圆心确定圆的位置,半径确定圆的大小,据此即可判断选项A;
轴对称图形,是指在平面内沿一条直线折叠,直线两旁的部分能够完全重合的图形,这条直线就叫做对称轴,即可判断选项B;
圆的周长=圆周率×圆的直径(2×圆的半径),即可得出圆周率、圆的周长以及圆的直径之间的关系,即可判断选项C;
圆的直径是线段,圆的对称轴是直线,即可判断出选项D。
11.【答案】(1)错误
【考点】轴对称
【解析】【解答】解:人体内部器官图像不是轴对称图形。原题说法错误。
故答案为:错误。
【分析】人体内部左右里面是不相同的,所以人体内部器官图像不是轴对称图形。
12.【答案】(1)正
【考点】轴对称
【解析】【解答】解: 是从 对折后的纸上剪下来的图形。
故答案为:正确。
【分析】把左边的图形沿着对称轴折叠,其中,左半部分就是与之对应的右面纸上剪下来的。
13.【答案】(1)错误
【考点】轴对称图形的对称轴数量及位置
【解析】【解答】解:五角星是轴对称图形,它有5条对称轴。原题说法错误。
故答案为:错误。
【分析】五角星的对称轴如图:
14.【答案】(1)错误
【考点】轴对称图形的对称轴数量及位置
【解析】【解答】解:长方形有2条对称轴,所以说法错误。
故答案为:错误。
【分析】轴对称图形,是指在平面内沿一条直线折叠,直线两旁的部分能够完全重合的图形,这条直线就叫做对称轴。长方形只有对应两边中点的连线是对称轴。
15.【答案】(1)正
【考点】轴对称
【解析】【解答】 轴对称图形中,对应点到对称轴的距离相等,此题说法正确。
故答案为:正确。
【分析】在轴对称图形中,对称轴两侧相对应的点到对称轴的距离相等,据此判断。
16.【答案】(1)正
【考点】轴对称图形的对称轴数量及位置
【解析】【解答】解:圆是轴对称图形,有无数条对称轴,直径所在的直线就是对称轴,所以每条对称轴都过圆心。
故答案为:正确。
【分析】圆是轴对称图形,有无数条对称轴,直径所在的直线就是对称轴,圆的直径有无数条,所以每条对称轴都过圆心。
17.【答案】(1)错误
【考点】轴对称
【解析】【解答】解:圆、长方形、正方形都是轴对称图形,三角形不一定是轴对称图形。
故答案为:错误。
【分析】不规则三角形不是轴对称图形。
18.【答案】(1)错误
【考点】轴对称;梯形的特征及分类
【解析】【解答】梯形可能是轴对称图形,等腰梯形是轴对称图形。
故答案为:错误。
【分析】如果一个图形沿着一条直线对折后两部分完全重合,那这样的图形就叫做轴对称图形,据此解答。
19.【答案】(1)错误
【考点】轴对称
【解析】【解答】字母A是轴对称图形。原题说法错误。
故答案为:错误。
【分析】一个图形沿着一条直线对折后两边能够完全重合,这个图形就是轴对称图形。
20.【答案】(1)正
【考点】轴对称图形的对称轴数量及位置
【解析】【解答】圆形有无数条对称轴。原题说法正确。
故答案为:正确。
【分析】一个圆形沿着过圆心的任意一条直线对折后两边都能完全重合,所以圆有无数条对称轴。
21.【答案】平行四边形
【考点】轴对称
【解析】【解答】长方形、正方形,平行四边形中不是轴对称图形的是平行四边形。
故答案为:平行四边形。
【分析】如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形。
22.【答案】4;2;无数
【考点】轴对称图形的对称轴数量及位置
【解析】【解答】解:正方形有4条对称轴,长方形有2条对称轴,圆形有无数条对称轴。
故答案为:4;2;无数。
【分析】轴对称图形是指平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形,其中这条直线叫做对称轴。
23.【答案】两;18.84;36
【考点】长方形的周长;轴对称图形的对称轴数量及位置;圆的周长
【解析】【解答】 左图中有两条对称轴;
如果圆的半径是3cm,那么每个圆的周长是3.14×3×2=18.84(cm),长方形的周长是(3×4+3×2)×2=36(cm)。
故答案为:两;18.84;36。
【分析】观察图可知,这个图形是由长方形与两个圆组合成的,有两条对称轴,分别是两条长和两条宽的中点所在的直线;
已知圆的半径,要求圆的周长,用公式:C=2πr,据此列式解答;
观察图可知,长方形的长是圆的半径的4倍,宽是圆的半径的2倍,先求出长方形的长与宽,然后用公式:长方形的周长=(长+宽)×2,据此列式解答。
24.【答案】2;0;3
【考点】轴对称图形的对称轴数量及位置
【解析】【解答】解:长方形有2条对称轴,平行四边形有0条对称轴,等边三角形有3条对称轴。
故答案为:2;0;3。
【分析】 轴对称图形,是指在平面内沿一条直线折叠,直线两旁的部分能够完全重合的图形,这条直线就叫做对称轴。本题中长方形的对称轴为两组对边中点的连线;平行四边形没有对称轴;等边三角形的三条中线是对称轴,本题据此解答。
25.【答案】4
【考点】轴对称图形的对称轴数量及位置
【解析】【解答】因为正方形沿两组对边的中线及其对角线所在的直线对折,对折后的两部分都能完全重合,
则正方形是轴对称图形,两组对边的中线及其对角线所在的直线就是其对称轴,
所以说正方形有4条对称轴.
故答案为:4.
【分析】轴对称图形,是指在平面内沿一条直线折叠,直线两旁的部分能够完全重合的图形,这条直线就叫做对称轴。本题中将正方形折叠使其两部分完全重合,找出这样的所有直线,即可得出答案。
26.【答案】2;4;无数
【考点】轴对称图形的对称轴数量及位置
【解析】【解答】 长方形有2条对称轴,正方形有4条对称轴,圆形有无数条对称轴。
故答案为:2;4;无数。
【分析】如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫对称轴;判断一个图形是否是轴对称图形,关键是找它的对称轴,要想象沿着这条线翻折能不能重叠,据此找出题中各图形的对称轴。
27.【答案】24
【考点】利用平移巧算图形周长与面积
【解析】【解答】解:6×4=24(平方厘米)
故答案为:24。
【分析】用平移的方法,把左边的半圆向右平移6格,就变成了一个长6厘米,宽4厘米的长方形,用长×宽就得出了涂色部分的面积。
28.【答案】轴对称;轴对称;平移;轴对称
【考点】轴对称;平移与平移现象
【解析】【解答】解:
故答案为:轴对称;轴对称;平移;轴对称。
【分析】如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形,折痕所在的这条直线叫做对称轴;
物体或图形沿着某个方向移动了一定距离叫做平移。特点:大小、形状、方向不变,位置变化。
29.【答案】48
【考点】利用平移巧算图形周长与面积
【解析】【解答】解:9×2=18(厘米)
3×2=6(厘米)
(18+6)×2
=24×2
=48(厘米)
故答案为:48。
【分析】通过平移把这个图形的周长变成长18厘米,宽6厘米的长方形,长方形的周长=(长+宽)×2。
30.【答案】24
【考点】利用平移巧算图形周长与面积
【解析】【解答】解:6×4=24(cm2)
故答案为:24。
【分析】利用平移的方法, 阴影部分变成一个长方形,长方形的面积=长×宽。
31.【答案】(1)(6+3)×2=18(米)
(2)5×4=20(米)
【考点】长方形的周长;利用平移巧算图形周长与面积
【解析】【分析】(1)长方形周长=(长+宽)×2,据此解答;
(2)把右上角的两条短边向右向上平移,刚好是一个正方形,正方形周长=边长×4。
32.【答案】(1)(2,7)
(2)解:如图所示:
(3)解:如图所示:
【考点】作平移后的图形
【解析】【分析】(1)用数对表示位置时,前面一个数表示第几列,后面一个数表示第几行;
(2)作平移图形的方法:先确定要平移图形的关键点,确定平移的方向是朝哪移的,然后确定移动的长度(格子数),最后把各点连接成图;
(3)画轴对称图形的方法是:数出或量出图形的关键点到对称轴的距离,在对称轴的另一侧找出关键点的对应点,按照所给图形的顺序连接各点。
33.【答案】解:10×6=60(平方厘米)
答:阴影部分面积是60平方厘米。
【考点】长方形的面积;利用平移巧算图形周长与面积
【解析】【分析】把左边阴影部分向右平移与右边的阴影部分组合成一个长方形,长是10厘米、宽是6厘米,根据长方形面积公式计算阴影部分的总面积即可。
34.【答案】(1)
(2)
图形C左下角顶点的位置用数对表示是(3, 2)。
(3)
图形D的面积是(1.5)cm2。
【考点】图形的缩放;补全轴对称图形;作旋转后的图形
【解析】【解答】(1)如图所示:
(2)如图所示:
图形C左下角顶点的位置用数对表示是(3,2)。
(3)如图所示:
(1+2)×1÷2=1.5(cm2)。
故答案为:(1)
(2)
图形C左下角顶点的位置用数对表示是(3,2);
(3)
图形D的面积是(1.5)cm2。
【分析】 (1)已知图形A,在对称轴另一侧找到图形A对应个点,依次连接各点,由此画出轴对称图形B;
(2)以图形A左下角顶点为旋转中心,找出各点顺时针旋转90°后的对应点,再将这几个点依次连接,由此可以画出旋转后的图形C ;
(3)缩小后的图形D与原图形A对应线段长的比为1:2,原图各边长除以2,得到缩小后各边长度,梯形面积=(上底+下底)×高÷2,据此解答。
35.【答案】(1)北;10;东;北45
(2)4;86
(3)解:
【考点】轴对称图形的对称轴数量及位置;根据方向和距离确定物体的位置;圆的面积
【解析】【分析】(1)根据方向标,平面图上上北下南、左西右东,正方形边长是20,所以A距中心O的距离是10m,因为扇形的面积完全一样,所以A是边长的中点,所以B在东偏北45度方向上;
(2)四个扇形的圆心角都是90度,且半径都相等,所以4个扇形正好构成一个半径是10m的圆,阴影的面积=正方形的面积-圆的面积=20×20-π×102=400-314=86m2;
(3)把外围的扇形移动到中间拼成一个半径是10m的圆,也就是以中心点O为圆心,10m为半径画一个圆,剩余是绿植的部分。
试题分析部分
1、试卷总体分布分析
总分:113分
分值分布 客观题(占比) 58.0(51.3%)
主观题(占比) 55.0(48.7%)
题量分布 客观题(占比) 29(82.9%)
主观题(占比) 6(17.1%)
2、试卷题量分布分析
大题题型 题目量(占比) 分值(占比)
填空题 10(28.6%) 21.0(18.6%)
解答题 2(5.7%) 26.0(23.0%)
计算题 3(8.6%) 26.0(23.0%)
单选题 10(28.6%) 20.0(17.7%)
判断题 10(28.6%) 20.0(17.7%)
3、试卷难度结构分析
序号 难易度 占比
1 普通 (91.4%)
2 困难 (8.6%)
4、试卷知识点分析
序号 知识点(认知水平) 分值(占比) 对应题号
1 作旋转后的图形 15.0(13.3%) 34
2 圆的周长 5.0(4.4%) 10,23
3 长方形的面积 5.0(4.4%) 33
4 作平移后的图形 11.0(9.7%) 32
5 平移与平移现象 4.0(3.5%) 28
6 根据方向和距离确定物体的位置 11.0(9.7%) 35
7 利用平移巧算图形周长与面积 20.0(17.7%) 3,27,29,30,31,33
8 轴对称 31.0(27.4%) 1,2,4,5,6,8,10,11,12,15,17,18,19,21,28
9 轴对称图形的对称轴数量及位置 38.0(33.6%) 7,8,9,13,14,16,20,22,23,24,25,26,35
10 补全轴对称图形 15.0(13.3%) 34
11 圆的面积 11.0(9.7%) 35
12 梯形的特征及分类 2.0(1.8%) 18
13 长方形的周长 13.0(11.5%) 23,31
14 圆、圆心、半径与直径的认识 2.0(1.8%) 10
15 图形的缩放 15.0(13.3%) 34
1 / 19
