抛物线及其标准方程
图片预览








文档简介
课件26张PPT。抛物线及其标准方程(一)请同学们思考两个问题1、我们对抛物线已有了哪些认识?2、二次函数的图像抛物线的
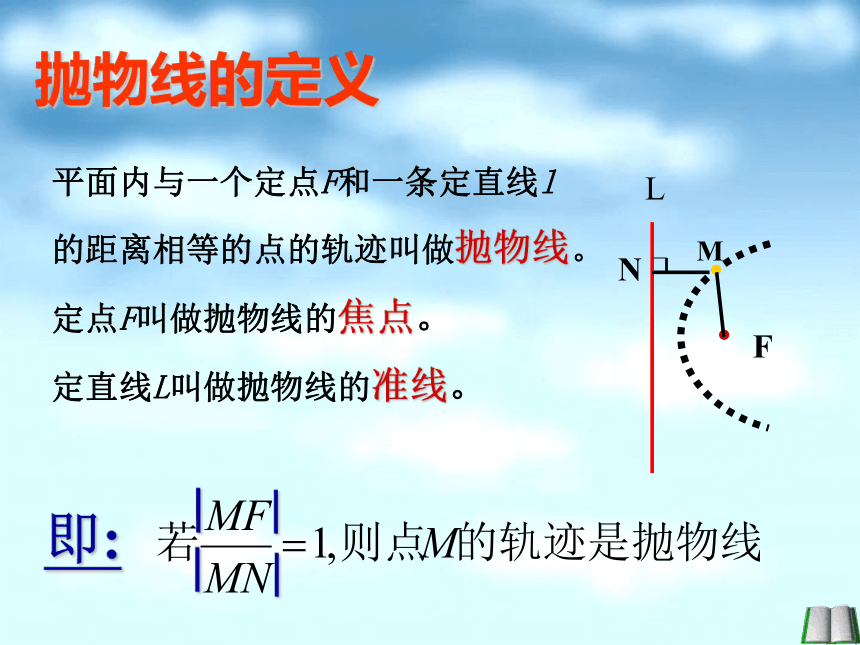
开口方向是什么? 在二次函数中研究的抛物线, 有开口向上或向下两种情形。生活中存在着各种形式的抛物线抛物线的生活实例投篮运动抛物线的生活实例探照灯的灯面你能说出动画演示作抛物线的依据吗?探索内容平面内与一个定点F和一条定直线l
的距离相等的点的轨迹叫做抛物线。
定点F叫做抛物线的焦点。
定直线L叫做抛物线的准线。
抛物线的定义求曲线方程的基本步骤是怎样的?抛物线标准方程的推导回顾求曲线方程的一般步骤是:1、建立直角坐标系,设动点为(x,y)2、写出适合条件的x,y的关系式3、列方程4、化简5、(证明)设焦点到准线的距离为常数P(P>0)如何建立坐标系,求出抛物线的标准方程呢?抛物线标准方程的推导试一试?KK设︱KF︱= p设动点M的坐标为(x,y) 由抛物线的定义可知,解:如图,取过焦点F且垂直于准线L的直线为x轴,线段KF的中垂线为y轴
抛物线标准方程的推导( p> 0)抛物线标准方程的推导如图,若以准线所在直线为y轴, 则焦点F(P,0),准线L:x=0
由抛物线的定义,可导出
抛物线方程为
y2 = 2p(x- )(p>0)比较之下,显然方程
y2 = 2px(p>0)更为简单 方程 y2 = 2px(p>0)叫做
抛物线的标准方程其中 p 为正常数,它的几何意义是:
焦 点 到 准 线 的 距 离抛物线的标准方程但是,一条抛物线,由于它在坐标平面内的位置不同,方程也不同,所以抛物线的标准方程还有其它形式。
方程 y2 = 2px(p>0)表示的抛物线,其焦点 位于X轴的正半轴上,其准线交于X轴的负半轴抛物线的标准方程抛物线的标准方程还有哪些形式?抛物线的标准方程其它形式的抛物线的焦点与准线呢?向右
向左
向上
向下
怎样把抛物线的位置特征(标准位置)和方程特征(标准方程)统一起来?抛物线的标准方程抛物线方程
左右型标准方程为
y2 =+ 2px
(p>0)开口向右:
y2 =2px(x≥ 0)开口向左:
y2 = -2px(x≤ 0)
标准方程为
x2 =+ 2py
(p>0)开口向上:
x2 =2py (y≥ 0)开口向下:
x2 = -2py (y≤0)抛物线的标准方程
上下型例1:求下列抛物线的焦点坐标和准线方程:
(1)y2 = 20x (2)y=2x2
(3)2y2 +5x =0 (4)x2 +8y =0(5,0)x= -5(0,-2)y=2课堂练习注意:求抛物线的焦点一定要先把抛物线化为标准形式例2:根据下列条件,写出抛物线的标准方程:(1)焦点是F(3,0)(3)焦点到准线的距离是2解:y2 =12x解:y2 =x解:y2 =4x或y2 = -4x
或x2 =4y或x2 = -4y课堂练习反思研究先定位,后定量
例3:求过点A(-3,2)的抛物线的
标准方程。课堂练习例4:已知抛物线方程为x=ay2(a≠0),讨论 抛物线的开口方向、焦点坐标和准线方程?课堂练习3。抛物线的标准方程类型与图象特征的
对应关系及判断方法2。抛物线的标准方程与其焦点、准线4。注重数形结合的思想 1。抛物线的定义课堂小结5。注重分类讨论的思想二 次 函 数 的 最 值感谢各位评委
老师的光临!同学们再见!
开口方向是什么? 在二次函数中研究的抛物线, 有开口向上或向下两种情形。生活中存在着各种形式的抛物线抛物线的生活实例投篮运动抛物线的生活实例探照灯的灯面你能说出动画演示作抛物线的依据吗?探索内容平面内与一个定点F和一条定直线l
的距离相等的点的轨迹叫做抛物线。
定点F叫做抛物线的焦点。
定直线L叫做抛物线的准线。
抛物线的定义求曲线方程的基本步骤是怎样的?抛物线标准方程的推导回顾求曲线方程的一般步骤是:1、建立直角坐标系,设动点为(x,y)2、写出适合条件的x,y的关系式3、列方程4、化简5、(证明)设焦点到准线的距离为常数P(P>0)如何建立坐标系,求出抛物线的标准方程呢?抛物线标准方程的推导试一试?KK设︱KF︱= p设动点M的坐标为(x,y) 由抛物线的定义可知,解:如图,取过焦点F且垂直于准线L的直线为x轴,线段KF的中垂线为y轴
抛物线标准方程的推导( p> 0)抛物线标准方程的推导如图,若以准线所在直线为y轴, 则焦点F(P,0),准线L:x=0
由抛物线的定义,可导出
抛物线方程为
y2 = 2p(x- )(p>0)比较之下,显然方程
y2 = 2px(p>0)更为简单 方程 y2 = 2px(p>0)叫做
抛物线的标准方程其中 p 为正常数,它的几何意义是:
焦 点 到 准 线 的 距 离抛物线的标准方程但是,一条抛物线,由于它在坐标平面内的位置不同,方程也不同,所以抛物线的标准方程还有其它形式。
方程 y2 = 2px(p>0)表示的抛物线,其焦点 位于X轴的正半轴上,其准线交于X轴的负半轴抛物线的标准方程抛物线的标准方程还有哪些形式?抛物线的标准方程其它形式的抛物线的焦点与准线呢?向右
向左
向上
向下
怎样把抛物线的位置特征(标准位置)和方程特征(标准方程)统一起来?抛物线的标准方程抛物线方程
左右型标准方程为
y2 =+ 2px
(p>0)开口向右:
y2 =2px(x≥ 0)开口向左:
y2 = -2px(x≤ 0)
标准方程为
x2 =+ 2py
(p>0)开口向上:
x2 =2py (y≥ 0)开口向下:
x2 = -2py (y≤0)抛物线的标准方程
上下型例1:求下列抛物线的焦点坐标和准线方程:
(1)y2 = 20x (2)y=2x2
(3)2y2 +5x =0 (4)x2 +8y =0(5,0)x= -5(0,-2)y=2课堂练习注意:求抛物线的焦点一定要先把抛物线化为标准形式例2:根据下列条件,写出抛物线的标准方程:(1)焦点是F(3,0)(3)焦点到准线的距离是2解:y2 =12x解:y2 =x解:y2 =4x或y2 = -4x
或x2 =4y或x2 = -4y课堂练习反思研究先定位,后定量
例3:求过点A(-3,2)的抛物线的
标准方程。课堂练习例4:已知抛物线方程为x=ay2(a≠0),讨论 抛物线的开口方向、焦点坐标和准线方程?课堂练习3。抛物线的标准方程类型与图象特征的
对应关系及判断方法2。抛物线的标准方程与其焦点、准线4。注重数形结合的思想 1。抛物线的定义课堂小结5。注重分类讨论的思想二 次 函 数 的 最 值感谢各位评委
老师的光临!同学们再见!
