物理人教版(2019)必修第二册5.4抛体运动规律(共23张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第二册5.4抛体运动规律(共23张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-22 19:36:28 | ||
图片预览







文档简介
(共23张PPT)
第五章 抛体运动
第 4 节 抛体运动的规律
1.掌握平抛运动的一般研究方法。
2.掌握平抛运动的位移与速度。
3.了解斜抛运动的特点和分析方法。
4.掌握平抛运动的规律,会用平抛运动的知识处理实际问题。
学习目标
top 1
top 2
top 3
目录 /CONTENTS
平抛运动的速度
平抛运动的位移和轨迹
平抛运动的重要推论
top 3
一般的抛体运动
请观看视频,你认为左边的运动员为什么会输?思考:在乒乓球比赛中,你是否曾为乒乓球下网或者出界而感到惋惜?如果运动员沿水平方向击球,在不计空气阻力的情况下,要使乒乓球既能过网,又不出界,需要考虑哪些因素?如何估算球落地时速度大小?
引入新课
上节知识回顾
1.定义:物体以一定的初速度沿水平方向抛出,只受重力作用的曲线运动
2.条件:①初速度沿水平方向 ②只受重力作用
3.运动性质:匀变速曲线运动(a=g)
4.受力特点:
平抛运动
水平方向:不受力
竖直方向:仅受重力
5.研究方法----运动的合成与分解
一、平抛运动的速度
一物体以初速度v0水平抛出,不计空气阻力,经过时间t运动到P点,求此时P的速度?
第一步:建立直角坐系标
以抛出点为原点,以初速度v0作为x的方向,竖直方向为y轴方向。
第二步:将速度分解
将速度分解在x轴方向和y轴方向上。
思考:如何确定两个分速度的大小?
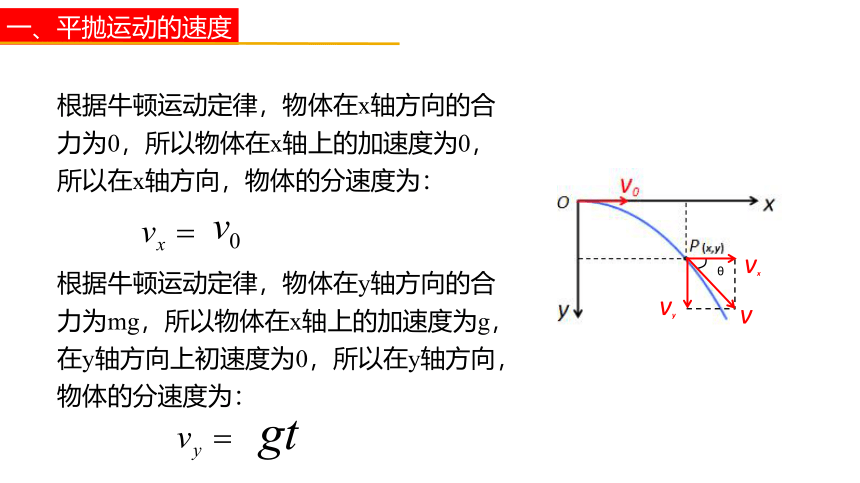
根据牛顿运动定律,物体在x轴方向的合力为0,所以物体在x轴上的加速度为0,所以在x轴方向,物体的分速度为:
vx
vy
v
θ
根据牛顿运动定律,物体在y轴方向的合力为mg,所以物体在x轴上的加速度为g,在y轴方向上初速度为0,所以在y轴方向,物体的分速度为:
一、平抛运动的速度
根据牛顿运动定律,物体在x轴方向的合力为0,所以物体在x轴上的加速度为0,所以在x轴方向,物体的分速度为:
vx
vy
v
θ
根据牛顿运动定律,物体在y轴方向的合力为mg,所以物体在x轴上的加速度为g,在y轴方向上初速度为0,所以在y轴方向,物体的分速度为:
一、平抛运动的速度
【例题1】将一个物体以10 m/s的速度从10 m的高度水平抛出,落地时它的速度方向与水平地面的夹角θ是多少?不计空气阻力,g取10 m/s2。
分析:物体的水平分速度已知,竖直分速度可以由自由落体运动的高度求出。两者相比,即可求得tanθ,进而求出夹角θ。
一、平抛运动的速度
解:以抛出时物体的位置O为原点,建立平面直角坐标系。x轴沿初速度方向,y轴竖直向下。
落地时,物体在水平方向的分速度
根据匀变速直线运动的规律,落地时物体在竖直方向的分速度满足以下关系
一、平抛运动的速度
二、平抛运动的位移和轨迹
(3)位移的方向
(1)根据上面的分析,可以知道平抛运动在水平方向得分位移:
(2)根据上面的分析,可以知道平抛运动在竖直方向得分位移:
(3)合位移:
二、平抛运动的位移和轨迹
——平抛运动的轨迹是一条抛物线
水平方向:匀速直线运动
竖直方向:自由落体运动
消去 t 得:
2.平抛的轨迹:
二、平抛运动的位移和轨迹
【例题2】 如图,某同学利用无人机玩“投弹”游戏。无 人机以 v0 = 2 m/s 的速度水平向右匀速飞行,在某时 刻释放了一个小球。此时无人机到水平地面的距离 h = 20 m,空气阻力忽略不计,g 取 10 m/s2 。
(1)求小球下落的时间。
(2)求小球释放点与落地点之间的水平距离。
解:(1)以小球从无人机释放时的位置为原点O建立平面直角坐标系,x 轴沿初速度方向,y轴竖直向下。设小球的落地点为P,下落的时间为t,则满足
所以小球落地的时间
(2)因此,小球落地点与释放点之间的水平距离
三、平抛运动的重要推论
①运动时间:由 ,得 ,即物体在空中的飞行时间仅取决于下落的高度,与初速度v0无关。
②落地的水平距离:由 , 得 ,即落地的水平距离与初速度v0和下落高度h有关,与其他因素无关。
③落地速度: ,即落地速度也只与初速度v0和下落高度h有关。
三、平抛运动的重要推论
④做平抛(或类平抛)运动的物体,设其末速度方向与水平方向的夹角为θ,位移方向与水平方向的夹角为α,则在任意时刻、任意位置有tanθ=2tanα。
证明:
(θ≠2α)
得出:
三、平抛运动的重要推论
⑤做平抛(或类平抛)运动的物体在任意时刻的瞬时速度的反向延长线一定通过此时水平位移的中点,如图所示。
证明:设平抛物体的初速度为v0,从抛出点(原点O)到A点的时间为t,A点的坐标为(x,y),B点的坐标为(x′,0),tanθ=2tanα
即 = ,解得x′= 。
OC=2OB
C
即B为OC中点
四、一般的抛体运动
1、斜抛运动的定义:如果物体被抛出时的速度v0不沿水平方向,而是斜向上方或斜向下方,这种抛体运动叫斜抛运动。
(1)受力特点:在水平方向不受力,加速度为0;在竖直方向只受重力,加速度为g。
(2)初速度特点:以斜上抛运动为例,把斜向上方的初速度分解到水平方向和竖直方向,如图所示,水平方向以vx=v0cosθ 做匀速直线运动;竖直方向以v0sinθ为初速度做竖直上抛运动。
2、斜抛运动的特点
三、平抛运动的重要推论
3.斜抛运动的速度和位移的规律
(1)轨迹:(如图)
(2)水平速度:
水平位移:
(3)竖直速度:
竖直位移:
x=v0tcos
vx=v0cos
vy=v0sin - gt
斜抛运动
水平方向vx=v0cosθ
位移
速度
竖直方向
水平方向 x=v0tcos
竖直方向
斜上抛取“-”,斜下抛取“+”。
课堂小结
课堂小结
1.从离地高30 m处水平抛出一个物体,1s末物体的速度大小为20 m/s,取g=10 m/s2。求:
(1)物体抛出时的初速度大小;
(2)3 s末物体的速度与水平方向的夹角。
解析:(1)由平抛运动的规律知
1 s末v=20 m/s,vy=gt=10 m/s
解得v0=vx=10 m/s
(2)1s末物体的速度与水平方向的夹角的 θ=30°
课堂小结
2.飞机在高出地面0.81km的高度,以2.5×102km/h速度水平飞行,为了使飞机上投下的的炸弹落在指定目标上,应该在与轰炸目标的水平距离为多远的地方投弹。
0.88km
课堂小结
3.一门大炮的炮筒与水平面的夹角β=30°,当炮弹以初速度v0=300 m/s的速度发出,炮弹能否击中离大炮7 500 m远的目标?(g取10 m/s2)
解析:炮弹发出后将做斜抛运动,如图所示,
vx=v0cos 30°=300× m/s=150 m/s,
vy=v0sin 30°=300× m/s=150 m/s,
炮弹飞行的总时间为t= =30 s。故炮弹飞行的水平距离为x=vxt=150×30 m≈7 794 m7 794 m>7 500 m,故不能击中7 500 m远的目标。
非常感谢您的观看
第五章 抛体运动
第 4 节 抛体运动的规律
1.掌握平抛运动的一般研究方法。
2.掌握平抛运动的位移与速度。
3.了解斜抛运动的特点和分析方法。
4.掌握平抛运动的规律,会用平抛运动的知识处理实际问题。
学习目标
top 1
top 2
top 3
目录 /CONTENTS
平抛运动的速度
平抛运动的位移和轨迹
平抛运动的重要推论
top 3
一般的抛体运动
请观看视频,你认为左边的运动员为什么会输?思考:在乒乓球比赛中,你是否曾为乒乓球下网或者出界而感到惋惜?如果运动员沿水平方向击球,在不计空气阻力的情况下,要使乒乓球既能过网,又不出界,需要考虑哪些因素?如何估算球落地时速度大小?
引入新课
上节知识回顾
1.定义:物体以一定的初速度沿水平方向抛出,只受重力作用的曲线运动
2.条件:①初速度沿水平方向 ②只受重力作用
3.运动性质:匀变速曲线运动(a=g)
4.受力特点:
平抛运动
水平方向:不受力
竖直方向:仅受重力
5.研究方法----运动的合成与分解
一、平抛运动的速度
一物体以初速度v0水平抛出,不计空气阻力,经过时间t运动到P点,求此时P的速度?
第一步:建立直角坐系标
以抛出点为原点,以初速度v0作为x的方向,竖直方向为y轴方向。
第二步:将速度分解
将速度分解在x轴方向和y轴方向上。
思考:如何确定两个分速度的大小?
根据牛顿运动定律,物体在x轴方向的合力为0,所以物体在x轴上的加速度为0,所以在x轴方向,物体的分速度为:
vx
vy
v
θ
根据牛顿运动定律,物体在y轴方向的合力为mg,所以物体在x轴上的加速度为g,在y轴方向上初速度为0,所以在y轴方向,物体的分速度为:
一、平抛运动的速度
根据牛顿运动定律,物体在x轴方向的合力为0,所以物体在x轴上的加速度为0,所以在x轴方向,物体的分速度为:
vx
vy
v
θ
根据牛顿运动定律,物体在y轴方向的合力为mg,所以物体在x轴上的加速度为g,在y轴方向上初速度为0,所以在y轴方向,物体的分速度为:
一、平抛运动的速度
【例题1】将一个物体以10 m/s的速度从10 m的高度水平抛出,落地时它的速度方向与水平地面的夹角θ是多少?不计空气阻力,g取10 m/s2。
分析:物体的水平分速度已知,竖直分速度可以由自由落体运动的高度求出。两者相比,即可求得tanθ,进而求出夹角θ。
一、平抛运动的速度
解:以抛出时物体的位置O为原点,建立平面直角坐标系。x轴沿初速度方向,y轴竖直向下。
落地时,物体在水平方向的分速度
根据匀变速直线运动的规律,落地时物体在竖直方向的分速度满足以下关系
一、平抛运动的速度
二、平抛运动的位移和轨迹
(3)位移的方向
(1)根据上面的分析,可以知道平抛运动在水平方向得分位移:
(2)根据上面的分析,可以知道平抛运动在竖直方向得分位移:
(3)合位移:
二、平抛运动的位移和轨迹
——平抛运动的轨迹是一条抛物线
水平方向:匀速直线运动
竖直方向:自由落体运动
消去 t 得:
2.平抛的轨迹:
二、平抛运动的位移和轨迹
【例题2】 如图,某同学利用无人机玩“投弹”游戏。无 人机以 v0 = 2 m/s 的速度水平向右匀速飞行,在某时 刻释放了一个小球。此时无人机到水平地面的距离 h = 20 m,空气阻力忽略不计,g 取 10 m/s2 。
(1)求小球下落的时间。
(2)求小球释放点与落地点之间的水平距离。
解:(1)以小球从无人机释放时的位置为原点O建立平面直角坐标系,x 轴沿初速度方向,y轴竖直向下。设小球的落地点为P,下落的时间为t,则满足
所以小球落地的时间
(2)因此,小球落地点与释放点之间的水平距离
三、平抛运动的重要推论
①运动时间:由 ,得 ,即物体在空中的飞行时间仅取决于下落的高度,与初速度v0无关。
②落地的水平距离:由 , 得 ,即落地的水平距离与初速度v0和下落高度h有关,与其他因素无关。
③落地速度: ,即落地速度也只与初速度v0和下落高度h有关。
三、平抛运动的重要推论
④做平抛(或类平抛)运动的物体,设其末速度方向与水平方向的夹角为θ,位移方向与水平方向的夹角为α,则在任意时刻、任意位置有tanθ=2tanα。
证明:
(θ≠2α)
得出:
三、平抛运动的重要推论
⑤做平抛(或类平抛)运动的物体在任意时刻的瞬时速度的反向延长线一定通过此时水平位移的中点,如图所示。
证明:设平抛物体的初速度为v0,从抛出点(原点O)到A点的时间为t,A点的坐标为(x,y),B点的坐标为(x′,0),tanθ=2tanα
即 = ,解得x′= 。
OC=2OB
C
即B为OC中点
四、一般的抛体运动
1、斜抛运动的定义:如果物体被抛出时的速度v0不沿水平方向,而是斜向上方或斜向下方,这种抛体运动叫斜抛运动。
(1)受力特点:在水平方向不受力,加速度为0;在竖直方向只受重力,加速度为g。
(2)初速度特点:以斜上抛运动为例,把斜向上方的初速度分解到水平方向和竖直方向,如图所示,水平方向以vx=v0cosθ 做匀速直线运动;竖直方向以v0sinθ为初速度做竖直上抛运动。
2、斜抛运动的特点
三、平抛运动的重要推论
3.斜抛运动的速度和位移的规律
(1)轨迹:(如图)
(2)水平速度:
水平位移:
(3)竖直速度:
竖直位移:
x=v0tcos
vx=v0cos
vy=v0sin - gt
斜抛运动
水平方向vx=v0cosθ
位移
速度
竖直方向
水平方向 x=v0tcos
竖直方向
斜上抛取“-”,斜下抛取“+”。
课堂小结
课堂小结
1.从离地高30 m处水平抛出一个物体,1s末物体的速度大小为20 m/s,取g=10 m/s2。求:
(1)物体抛出时的初速度大小;
(2)3 s末物体的速度与水平方向的夹角。
解析:(1)由平抛运动的规律知
1 s末v=20 m/s,vy=gt=10 m/s
解得v0=vx=10 m/s
(2)1s末物体的速度与水平方向的夹角的 θ=30°
课堂小结
2.飞机在高出地面0.81km的高度,以2.5×102km/h速度水平飞行,为了使飞机上投下的的炸弹落在指定目标上,应该在与轰炸目标的水平距离为多远的地方投弹。
0.88km
课堂小结
3.一门大炮的炮筒与水平面的夹角β=30°,当炮弹以初速度v0=300 m/s的速度发出,炮弹能否击中离大炮7 500 m远的目标?(g取10 m/s2)
解析:炮弹发出后将做斜抛运动,如图所示,
vx=v0cos 30°=300× m/s=150 m/s,
vy=v0sin 30°=300× m/s=150 m/s,
炮弹飞行的总时间为t= =30 s。故炮弹飞行的水平距离为x=vxt=150×30 m≈7 794 m7 794 m>7 500 m,故不能击中7 500 m远的目标。
非常感谢您的观看
